5.10: Electric Charges and Fields (Exercises)
( \newcommand{\kernel}{\mathrm{null}\,}\)
Conceptual Questions
5.2 Electric Charge
1. There are very large numbers of charged particles in most objects. Why, then, don’t most objects exhibit static electricity?
2. Why do most objects tend to contain nearly equal numbers of positive and negative charges?
3. A positively charged rod attracts a small piece of cork.
(a) Can we conclude that the cork is negatively charged?
(b) The rod repels another small piece of cork. Can we conclude that this piece is positively charged?
4. Two bodies attract each other electrically. Do they both have to be charged? Answer the same question if the bodies repel one another.
5. How would you determine whether the charge on a particular rod is positive or negative?
5.3 Conductors, Insulators, and Charging by Induction
6. An eccentric inventor attempts to levitate a cork ball by wrapping it with foil and placing a large negative charge on the ball and then putting a large positive charge on the ceiling of his workshop. Instead, while attempting to place a large negative charge on the ball, the foil flies off. Explain.
7. When a glass rod is rubbed with silk, it becomes positive and the silk becomes negative—yet both attract dust. Does the dust have a third type of charge that is attracted to both positive and negative? Explain.
8. Why does a car always attract dust right after it is polished? (Note that car wax and car tires are insulators.)
9. Does the uncharged conductor shown below experience a net electric force?
10. While walking on a rug, a person frequently becomes charged because of the rubbing between his shoes and the rug. This charge then causes a spark and a slight shock when the person gets close to a metal object. Why are these shocks so much more common on a dry day?
11. Compare charging by conduction to charging by induction.
12. Small pieces of tissue are attracted to a charged comb. Soon after sticking to the comb, the pieces of tissue are repelled from it. Explain.
13. Trucks that carry gasoline often have chains dangling from their undercarriages and brushing the ground. Why?
14. Why do electrostatic experiments work so poorly in humid weather?
15. Why do some clothes cling together after being removed from the clothes dryer? Does this happen if they’re still damp?
16. Can induction be used to produce charge on an insulator?
17. Suppose someone tells you that rubbing quartz with cotton cloth produces a third kind of charge on the quartz. Describe what you might do to test this claim.
18. A handheld copper rod does not acquire a charge when you rub it with a cloth. Explain why.
19. Suppose you place a charge q near a large metal plate.
(a) If q is attracted to the plate, is the plate necessarily charged?
(b) If q is repelled by the plate, is the plate necessarily charged?
5.4 Coulomb's Law
20. Would defining the charge on an electron to be positive have any effect on Coulomb’s law?
21. An atomic nucleus contains positively charged protons and uncharged neutrons. Since nuclei do stay together, what must we conclude about the forces between these nuclear particles?
22. Is the force between two fixed charges influenced by the presence of other charges?
5.5 Electric Field
23. When measuring an electric field, could we use a negative rather than a positive test charge?
24. During fair weather, the electric field due to the net charge on Earth points downward. Is Earth charged positively or negatively?
25. If the electric field at a point on the line between two charges is zero, what do you know about the charges?
26. Two charges lie along the x-axis. Is it true that the net electric field always vanishes at some point (other than infinity) along the x-axis?
5.6 Calculating Electric Fields of Charge Distributions
27. Give a plausible argument as to why the electric field outside an infinite charged sheet is constant.
28. Compare the electric fields of an infinite sheet of charge, an infinite, charged conducting plate, and infinite, oppositely charged parallel plates.
29. Describe the electric fields of an infinite charged plate and of two infinite, charged parallel plates in terms of the electric field of an infinite sheet of charge.
30. A negative charge is placed at the center of a ring of uniform positive charge. What is the motion (if any) of the charge? What if the charge were placed at a point on the axis of the ring other than the center?
5.7 Electric Field Lines
31. If a point charge is released from rest in a uniform electric field, will it follow a field line? Will it do so if the electric field is not uniform?
32. Under what conditions, if any, will the trajectory of a charged particle not follow a field line?
33. How would you experimentally distinguish an electric field from a gravitational field?
34. A representation of an electric field shows 10 field lines perpendicular to a square plate. How many field lines should pass perpendicularly through the plate to depict a field with twice the magnitude?
35. What is the ratio of the number of electric field lines leaving a charge 10q and a charge q?
5.8 Electric Dipoles
36. What are the stable orientation(s) for a dipole in an external electric field? What happens if the dipole is slightly perturbed from these orientations?
Problems
5.2 Electric Charge
37. Common static electricity involves charges ranging from nanocoulombs to microcoulombs.
(a) How many electrons are needed to form a charge of −2.00 nC?
(b) How many electrons must be removed from a neutral object to leave a net charge of 0.500μC?
38. If 1.80×1020 electrons move through a pocket calculator during a full day’s operation, how many coulombs of charge moved through it?
39. To start a car engine, the car battery moves 3.75×1021 electrons through the starter motor. How many coulombs of charge were moved?
40. A certain lightning bolt moves 40.0 C of charge. How many fundamental units of charge is this?
41. A 2.5-g copper penny is given a charge of −2.0×10−9C.
(a) How many excess electrons are on the penny?
(b) By what percent do the excess electrons change the mass of the penny?
42. A 2.5-g copper penny is given a charge of 4.0×10−9C.
(a) How many electrons are removed from the penny?
(b) If no more than one electron is removed from an atom, what percent of the atoms are ionized by this charging process?
5.3 Conductors, Insulators, and Charging by Induction
43. Suppose a speck of dust in an electrostatic precipitator has 1.0000×1012 protons in it and has a net charge of −5.00 nC (a very large charge for a small speck). How many electrons does it have?
44. An amoeba has 1.00×1016 protons and a net charge of 0.300 pC.
(a) How many fewer electrons are there than protons?
(b) If you paired them up, what fraction of the protons would have no electrons?
45. A 50.0-g ball of copper has a net charge of 2.00μC. What fraction of the copper’s electrons has been removed? (Each copper atom has 29 protons, and copper has an atomic mass of 63.5.)
46. What net charge would you place on a 100-g piece of sulfur if you put an extra electron on 1 in 1012 of its atoms? (Sulfur has an atomic mass of 32.1 u.)
47. How many coulombs of positive charge are there in 4.00 kg of plutonium, given its atomic mass is 244 and that each plutonium atom has 94 protons?
5.4 Coulomb's Law
48. Two point particles with charges +3μC and +5μC are held in place by 3-N forces on each charge in appropriate directions. (a) Draw a free-body diagram for each particle. (b) Find the distance between the charges.
49. Two charges +3μC and +12μC are fixed 1 m apart, with the second one to the right. Find the magnitude and direction of the net force on a −2-nC charge when placed at the following locations:
(a) halfway between the two
(b) half a meter to the left of the +3μC charge
(c) half a meter above the +12μC charge in a direction perpendicular to the line joining the two fixed charges
50. In a salt crystal, the distance between adjacent sodium and chloride ions is 2.82×10−10m. What is the force of attraction between the two singly charged ions?
51. Protons in an atomic nucleus are typically 10−15m apart. What is the electric force of repulsion between nuclear protons?
52. Suppose Earth and the Moon each carried a net negative charge −Q. Approximate both bodies as point masses and point charges.
(a) What value of Q is required to balance the gravitational attraction between Earth and the Moon?
(b) Does the distance between Earth and the Moon affect your answer? Explain.
(c) How many electrons would be needed to produce this charge?
53. Point charges q1=50μC and q2=−25μC are placed 1.0 m apart. What is the force on a third charge q3=20μC placed midway between q1 and q2?
54. Where must q3 of the preceding problem be placed so that the net force on it is zero?
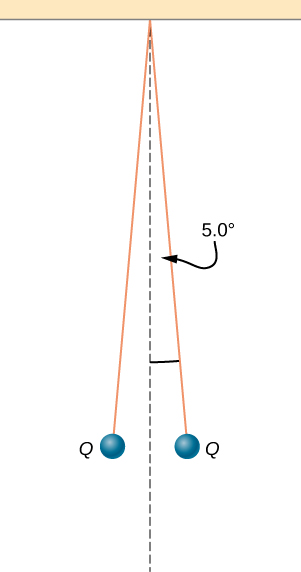
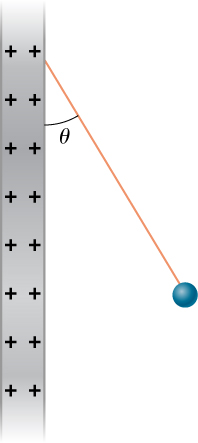
55. Two small balls, each of mass 5.0 g, are attached to silk threads 50 cm long, which are in turn tied to the same point on the ceiling, as shown below. When the balls are given the same charge Q, the threads hang at 5.0° to the vertical, as shown below. What is the magnitude of Q? What are the signs of the two charges?
56. Point charges Q1=2.0μC and Q2=4.0μC are located at →r1=(4.0ˆi−2.0ˆj+5.0ˆk)m and →r2=(8.0ˆi+5.0ˆj−9.0ˆk)m. What is the force of Q2 on Q1?
57. The net excess charge on two small spheres (small enough to be treated as point charges) is Q. Show that the force of repulsion between the spheres is greatest when each sphere has an excess charge Q/2. Assume that the distance between the spheres is so large compared with their radii that the spheres can be treated as point charges.
58. Two small, identical conducting spheres repel each other with a force of 0.050 N when they are 0.25 m apart. After a conducting wire is connected between the spheres and then removed, they repel each other with a force of 0.060 N. What is the original charge on each sphere?
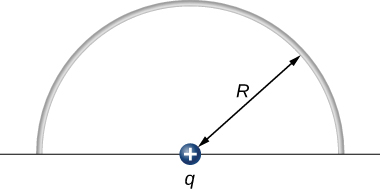
59. A charge q=2.0μC is placed at the point P shown below. What is the force on q?
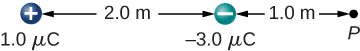
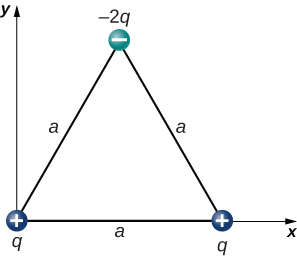
60. What is the net electric force on the charge located at the lower right-hand corner of the triangle shown here?
61. Two fixed particles, each of charge 5.0×10−6C, are 24 cm apart. What force do they exert on a third particle of charge −2.5×10−6C that is 13 cm from each of them?
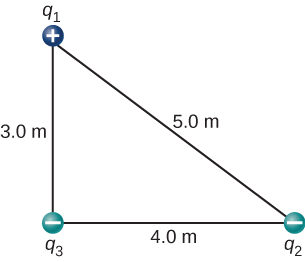
62. The charges q1=2.0×10−7C,q2=−4.0×10−7C, and q3=−1.0×10−7C are placed at the corners of the triangle shown below. What is the force on q1?
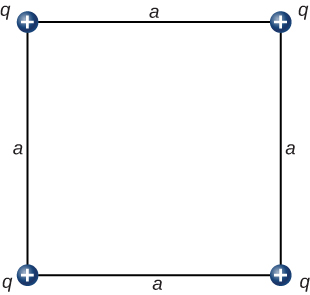
63. What is the force on the charge q at the lower-right-hand corner of the square shown here?
64. Point charges q1=10μC and q2=−30μC are fixed at r1=(3.0ˆi−4.0ˆj)m and r2=(9.0ˆi+6.0ˆj)m. What is the force of q2 on q1?
5.5 Electric Field
65. A particle of charge 2.0×10−8C experiences an upward force of magnitude 4.0×10−6N when it is placed in a particular point in an electric field.
(a) What is the electric field at that point?
(b) If a charge q=−1.0×10−8C is placed there, what is the force on it?
66. On a typical clear day, the atmospheric electric field points downward and has a magnitude of approximately 100 N/C. Compare the gravitational and electric forces on a small dust particle of mass 2.0×10−15g that carries a single electron charge. What is the acceleration (both magnitude and direction) of the dust particle?
67. Consider an electron that is 10−10m10−10m from an alpha particle (q=3.2×10−19C).(q=3.2×10−19C).
(a) What is the electric field due to the alpha particle at the location of the electron?
(b) What is the electric field due to the electron at the location of the alpha particle?
(c) What is the electric force on the alpha particle? On the electron?
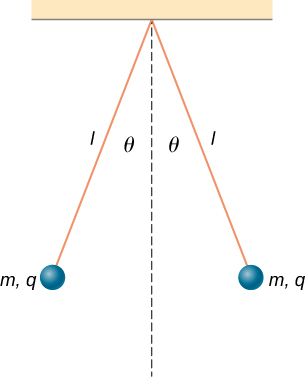
68. Each the balls shown below carries a charge q and has a mass m. The length of each thread is l, and at equilibrium, the balls are separated by an angle 2θ. How does θ vary with q and l? Show that θ satisfies \(\displaystyle sin(θ)^2tan(θ)=\frac{q^2}{16πε0gl^2m\).
69. What is the electric field at a point where the force on a −2.0×10−6−C charge is (4.0ˆi−6.0ˆj)×10−6N?
70. A proton is suspended in the air by an electric field at the surface of Earth. What is the strength of this electric field?
71. The electric field in a particular thundercloud is 2.0×105N/C. What is the acceleration of an electron in this field?
72. A small piece of cork whose mass is 2.0 g is given a charge of 5.0×10−7C. What electric field is needed to place the cork in equilibrium under the combined electric and gravitational forces?
73. If the electric field is 100N/C at a distance of 50 cm from a point charge q, what is the value of q?
74. What is the electric field of a proton at the first Bohr orbit for hydrogen (r=5.29×10−11m)? What is the force on the electron in that orbit?
75. (a) What is the electric field of an oxygen nucleus at a point that is 10−10m from the nucleus?
(b) What is the force this electric field exerts on a second oxygen nucleus placed at that point?
76. Two point charges, q1=2.0×10−7C and q2=−6.0×10−8C, are held 25.0 cm apart.
(a) What is the electric field at a point 5.0 cm from the negative charge and along the line between the two charges?
(b)What is the force on an electron placed at that point?
77. Point charges q1=50μC and q2=−25μC are placed 1.0 m apart.
(a) What is the electric field at a point midway between them?
(b) What is the force on a charge q3=20μC situated there?
78. Can you arrange the two point charges q1=−2.0×10−6C and q2=4.0×10−6C along the x-axis so that E=0 at the origin?
79. Point charges q1=q2=4.0×10−6C are fixed on the x-axis at x=−3.0m and x=3.0m. What charge q must be placed at the origin so that the electric field vanishes at x=0,y=3.0m?
5.6 Calculating Electric Fields of Charge Distributions
80. A thin conducting plate 1.0 m on the side is given a charge of −2.0×10−6C. An electron is placed 1.0 cm above the center of the plate. What is the acceleration of the electron?
81. Calculate the magnitude and direction of the electric field 2.0 m from a long wire that is charged uniformly at λ=4.0×10−6C/m.
82. Two thin conducting plates, each 25.0 cm on a side, are situated parallel to one another and 5.0 mm apart. If 1011 electrons are moved from one plate to the other, what is the electric field between the plates?
83. The charge per unit length on the thin rod shown below is λ. What is the electric field at the point P? (Hint: Solve this problem by first considering the electric field d→E at P due to a small segment dx of the rod, which contains charge dq=λdx. Then find the net field by integrating d→E over the length of the rod.)

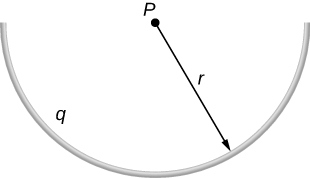
84. The charge per unit length on the thin semicircular wire shown below is λ. What is the electric field at the point P?
85. Two thin parallel conducting plates are placed 2.0 cm apart. Each plate is 2.0 cm on a side; one plate carries a net charge of 8.0μC, and the other plate carries a net charge of −8.0μC. What is the charge density on the inside surface of each plate? What is the electric field between the plates?
86. A thin conducting plate 2.0 m on a side is given a total charge of −10.0μC.
(a) What is the electric field 1.0cm above the plate?
(b) What is the force on an electron at this point?
(c) Repeat these calculations for a point 2.0 cm above the plate.
(d) When the electron moves from 1.0 to 2,0 cm above the plate, how much work is done on it by the electric field?
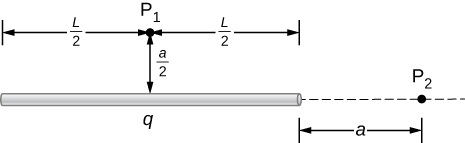
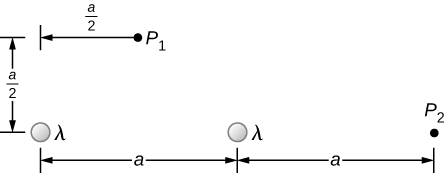
87. A total charge q is distributed uniformly along a thin, straight rod of length L (see below). What is the electric field at P1? At P2?
88. Charge is distributed along the entire x-axis with uniform density λ. How much work does the electric field of this charge distribution do on an electron that moves along the y-axis from y=a to y=b?
89. Charge is distributed along the entire x-axis with uniform density λx and along the entire y-axis with uniform density λy. Calculate the resulting electric field at
(a) →r=aˆi+bˆj and
(b) →r=cˆk.
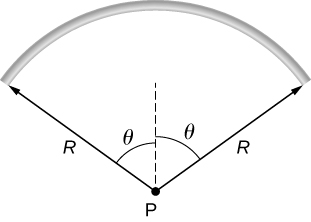
90. A rod bent into the arc of a circle subtends an angle 2θ at the center P of the circle (see below). If the rod is charged uniformly with a total charge Q, what is the electric field at P?.
91. A proton moves in the electric field →E=200ˆiN/C. (a) What are the force on and the acceleration of the proton? (b) Do the same calculation for an electron moving in this field.
92. An electron and a proton, each starting from rest, are accelerated by the same uniform electric field of 200 N/C. Determine the distance and time for each particle to acquire a kinetic energy of 3.2×10−16J.
93. A spherical water droplet of radius 25μm carries an excess 250 electrons. What vertical electric field is needed to balance the gravitational force on the droplet at the surface of the earth?
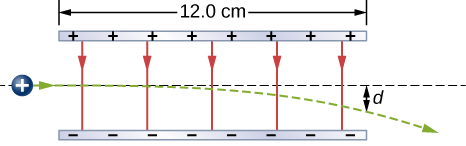
94. A proton enters the uniform electric field produced by the two charged plates shown below. The magnitude of the electric field is 4.0×105N/C, and the speed of the proton when it enters is 1.5×107m/s. What distance d has the proton been deflected downward when it leaves the plates?
95. Shown below is a small sphere of mass 0.25 g that carries a charge of 9.0×10−10C. The sphere is attached to one end of a very thin silk string 5.0 cm long. The other end of the string is attached to a large vertical conducting plate that has a charge density of 30×10−6C/m2. What is the angle that the string makes with the vertical?
96. Two infinite rods, each carrying a uniform charge density λ, are parallel to one another and perpendicular to the plane of the page. (See below.) What is the electrical field at P1? At P2?
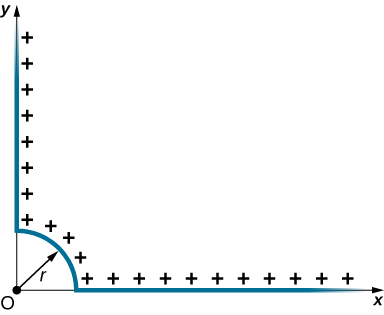
97. Positive charge is distributed with a uniform density λ along the positive x-axis from r to ∞, along the positive y-axis from r to ∞, and along a 90° arc of a circle of radius r, as shown below. What is the electric field at O?
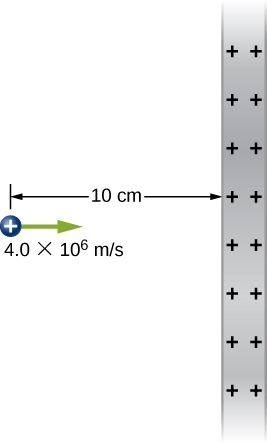
98. From a distance of 10 cm, a proton is projected with a speed of v=4.0×106m/s directly at a large, positively charged plate whose charge density is σ=2.0×10−5C/m2.. (See below.)
(a) Does the proton reach the plate?
(b) If not, how far from the plate does it turn around?
99. A particle of mass m and charge −q moves along a straight line away from a fixed particle of charge Q. When the distance between the two particles is r0,−q is moving with a speed v0.
(a) Use the work-energy theorem to calculate the maximum separation of the charges.
(b) What do you have to assume about v0 to make this calculation?
(c) What is the minimum value of v0 such that −q escapes from Q?
5.7 Electric Field Lines
100. Which of the following electric field lines are incorrect for point charges? Explain why.
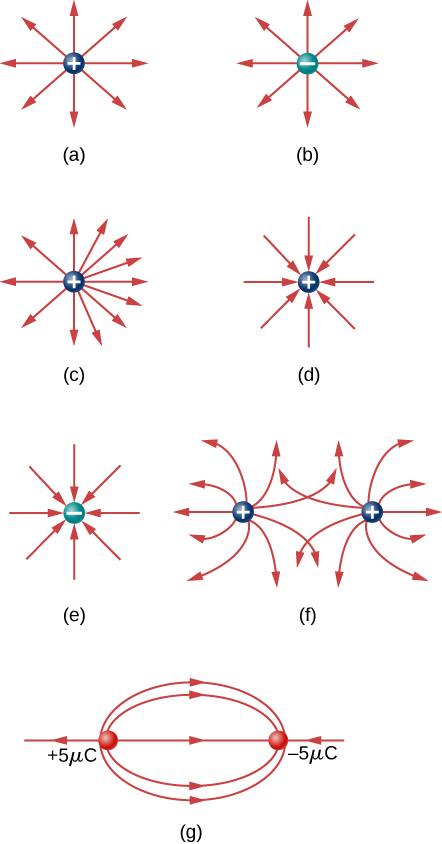
101. In this exercise, you will practice drawing electric field lines. Make sure you represent both the magnitude and direction of the electric field adequately. Note that the number of lines into or out of charges is proportional to the charges.
(a) Draw the electric field lines map for two charges +20μC and −20μC situated 5 cm from each other.
(b) Draw the electric field lines map for two charges +20μC and +20μC situated 5 cm from each other.
(c) Draw the electric field lines map for two charges +20μC and −30μC situated 5 cm from each other.
102. Draw the electric field for a system of three particles of charges +1μC, +2μC and −3μC fixed at the corners of an equilateral triangle of side 2 cm.
103. Two charges of equal magnitude but opposite sign make up an electric dipole. A quadrupole consists of two electric dipoles that are placed anti-parallel at two edges of a square as shown. Draw the electric field of the charge distribution.
104. Suppose the electric field of an isolated point charge decreased with distance as 1/r2+δ rather than as 1/r2. Show that it is then impossible to draw continuous field lines so that their number per unit area is proportional to E.
5.8 Electric Dipoles
105. Consider the equal and opposite charges shown below. (a) Show that at all points on the x-axis for which |x|≫a,E≈Qa/2πε0x3. (b) Show that at all points on the y-axis for which |y|≫a,E≈Qa/πε0y3.
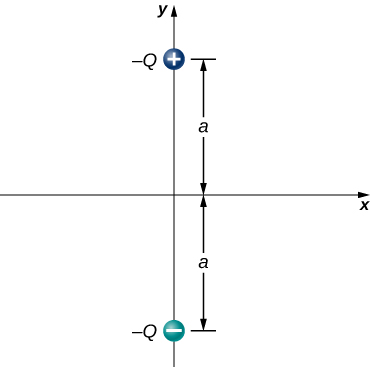
106. (a) What is the dipole moment of the configuration shown above? If Q=4.0μC,
(b) what is the torque on this dipole with an electric field of 4.0×105N/Cˆi?
(c) What is the torque on this dipole with an electric field of −4.0×105N/Cˆi?
(d) What is the torque on this dipole with an electric field of ±4.0×105N/Cˆj?
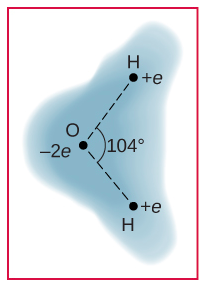
107. A water molecule consists of two hydrogen atoms bonded with one oxygen atom. The bond angle between the two hydrogen atoms is 104° (see below). Calculate the net dipole moment of a hypothetical water molecule where the charge at the oxygen molecule is −2e and at each hydrogen atom is +e. The net dipole moment of the molecule is the vector sum of the individual dipole moment between the two O-Hs. The separation O-H is 0.9578 angstroms.
Additional Problems
108. Point charges q1=2.0μC and q1=4.0μC are located at r1=(4.0ˆi−2.0ˆj+2.0ˆk)m and r2=(8.0ˆi+5.0ˆj−9.0ˆk)m. What is the force of q2 on q1?
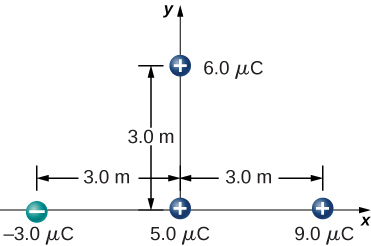
109. What is the force on the 5.0-μC charges shown below?
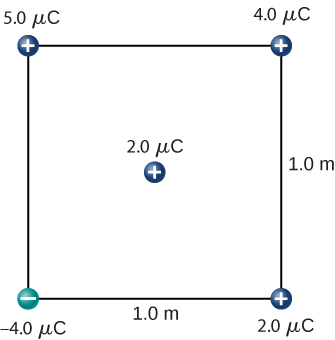
110. What is the force on the 2.0-μC charge placed at the center of the square shown below?
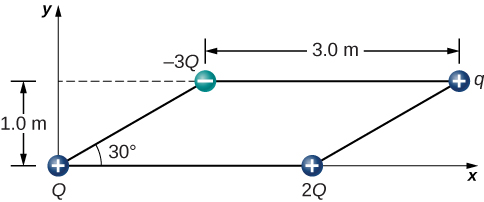
111. Four charged particles are positioned at the corners of a parallelogram as shown below. If q=5.0μC and Q=8.0μC, what is the net force on q?
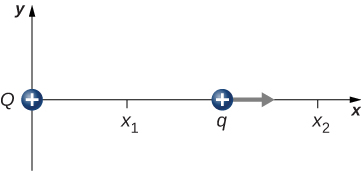
112. A charge Q is fixed at the origin and a second charge q moves along the x-axis, as shown below. How much work is done on q by the electric force when q moves from x1 to x2?
113. A charge q=−2.0μC is released from rest when it is 2.0 m from a fixed charge Q=6.0μC. What is the kinetic energy of q when it is 1.0 m from Q?
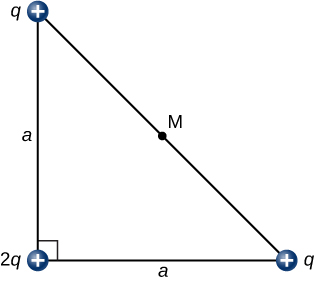
114. What is the electric field at the midpoint M of the hypotenuse of the triangle shown below?
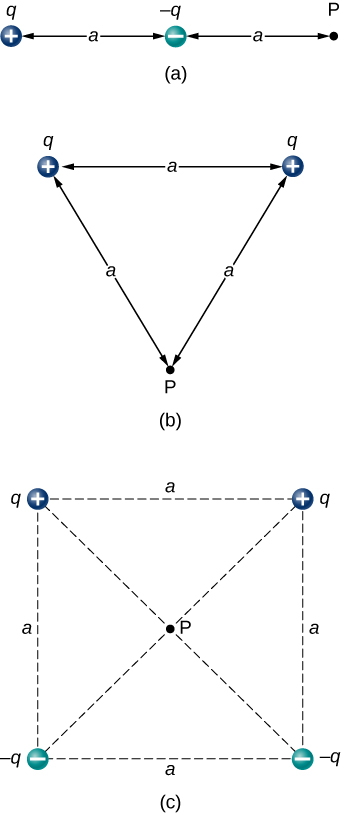
115. Find the electric field at P for the charge configurations shown below.
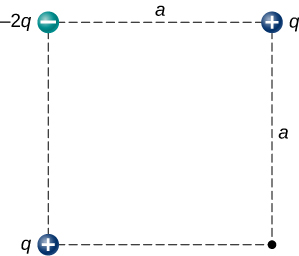
116. (a) What is the electric field at the lower-right-hand corner of the square shown below? (b) What is the force on a charge q placed at that point?
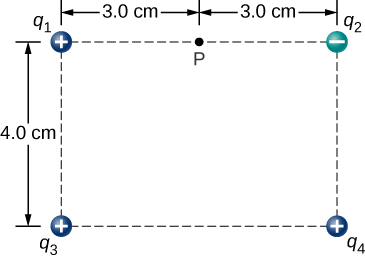
117. Point charges are placed at the four corners of a rectangle as shown below: q1=2.0×10−6C,q2=−2.0×10−6C,q3=4.0×10−6C, and q4=1.0×10−6C. What is the electric field at P?
118. Three charges are positioned at the corners of a parallelogram as shown below. (a) If Q=8.0μC, what is the electric field at the unoccupied corner? (b) What is the force on a 5.0-μC charge placed at this corner?
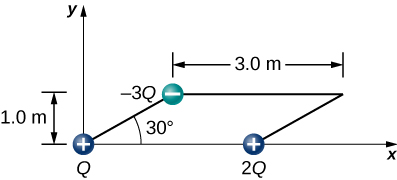
119. A positive charge q is released from rest at the origin of a rectangular coordinate system and moves under the influence of the electric field →E=E0(1+x/a)ˆi. What is the kinetic energy of q when it passes through x=3a?
120. A particle of charge −q and mass m is placed at the center of a uniformaly charged ring of total charge Q and radius R. The particle is displaced a small distance along the axis perpendicular to the plane of the ring and released. Assuming that the particle is constrained to move along the axis, show that the particle oscillates in simple harmonic motion with a frequency f=12π√qQ4πε0mR3.
121. Charge is distributed uniformly along the entire y-axis with a density yλ and along the positive x-axis from x=a to x=b with a density λx. What is the force between the two distributions?
122. The circular arc shown below carries a charge per unit length λ=λ0cosθ, where θ is measured from the x-axis. What is the electric field at the origin?
123. Calculate the electric field due to a uniformly charged rod of length L, aligned with the x-axis with one end at the origin; at a point P on the z-axis.
124. The charge per unit length on the thin rod shown below is λ. What is the electric force on the point charge q? Solve this problem by first considering the electric force d→F on q due to a small segment dx of the rod, which contains charge λdx. Then, find the net force by integrating d→F over the length of the rod.
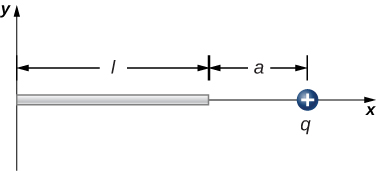
125. The charge per unit length on the thin rod shown here is λ. What is the electric force on the point charge q? (See the preceding problem.)
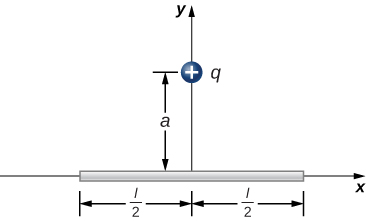
126. The charge per unit length on the thin semicircular wire shown below is λ. What is the electric force on the point charge q? (See the preceding problems.)