8.6: Molecular Model of a Dielectric

Learning Objectives

By the end of this section, you will be able to:

• Explain the polarization of a dielectric in a uniform electrical field
• Describe the effect of a polarized dielectric on the electrical field between capacitor plates
• Explain dielectric breakdown

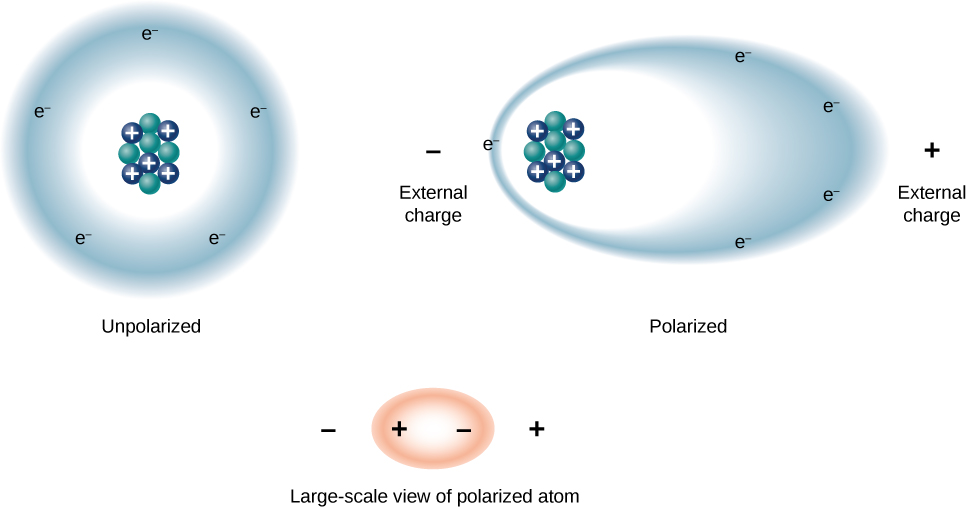
We can understand the effect of a dielectric on capacitance by looking at its behavior at the molecular level. As we have seen in earlier chapters, in general, all molecules can be classified as either polar or nonpolar. There is a net separation of positive and negative charges in an isolated polar molecule, whereas there is no charge separation in an isolated nonpolar molecule (Figure \(\PageIndex{1}\)). In other words, polar molecules have permanent electric-dipole moments and nonpolar molecules do not. For example, a molecule of water is polar, and a molecule of oxygen is nonpolar. Nonpolar molecules can become polar in the presence of an external electrical field, which is called induced polarization.

Figure \(\PageIndex{1}\): The concept of polarization: In an unpolarized atom or molecule, a negatively charged electron cloud is evenly distributed around positively charged centers, whereas a polarized atom or molecule has an excess of negative charge at one side so that the other side has an excess of positive charge. However, the entire system remains electrically neutral. The charge polarization may be caused by an external electrical field. Some molecules and atoms are permanently polarized (electric dipoles) even in the absence of an external electrical field (polar molecules and atoms).

Let’s first consider a dielectric composed of polar molecules. In the absence of any external electrical field, the electric dipoles are oriented randomly, as illustrated in Figure \(\PageIndex{2a}\). However, if the dielectric is placed in an external electrical field \(\vec{E}_0\), the polar molecules align with the external field, as shown in \(\PageIndex{2b}\) of the figure. Opposite charges on adjacent dipoles within the volume of dielectric neutralize each other, so there is no net charge within the dielectric (see the dashed circles in part (b)). However, this is not the case very close to the upper and lower surfaces that border the dielectric (the region enclosed by the dashed rectangles in \(\PageIndex{2b}\), where the alignment does produce a net charge. Since the external electrical field merely aligns the dipoles, the dielectric as a whole is neutral, and the surface charges induced on its opposite faces are equal and opposite. These induced surface charges \(+Q_i\) and \(-Q_i\) produce an additional electrical field \(\vec{E}_i\) (an induced electrical field), which opposes the external field \(\vec{E}_0\), as illustrated in part (c).

Figure \(\PageIndex{2}\): A dielectric with polar molecules: (a) In the absence of an external electrical field; (b) in the presence of an external electrical field \(\vec{E}_0\). The dashed lines indicate the regions immediately adjacent to the capacitor plates. (c) The induced electrical field \(\vec{E}_i\) inside the dielectric produced by the induced surface charge \(Q_i\) of the dielectric. Note that, in reality, the individual molecules are not perfectly aligned with an external field because of thermal fluctuations; however, the average alignment is along the field lines as shown.

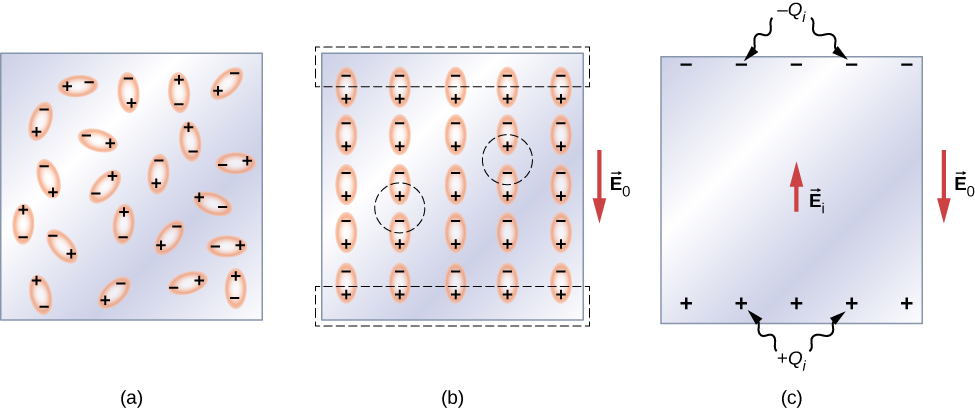
The same effect is produced when the molecules of a dielectric are nonpolar. In this case, a nonpolar molecule acquires an induced electric-dipole moment because the external field \(\vec{E}_0\) causes a separation between its positive and negative charges. The induced dipoles of the nonpolar molecules align with \(\vec{E}_0\) in the same way as the permanent dipoles of the polar molecules are aligned (shown in part (b)). Hence, the electrical field within the dielectric is weakened regardless of whether its molecules are polar or nonpolar.

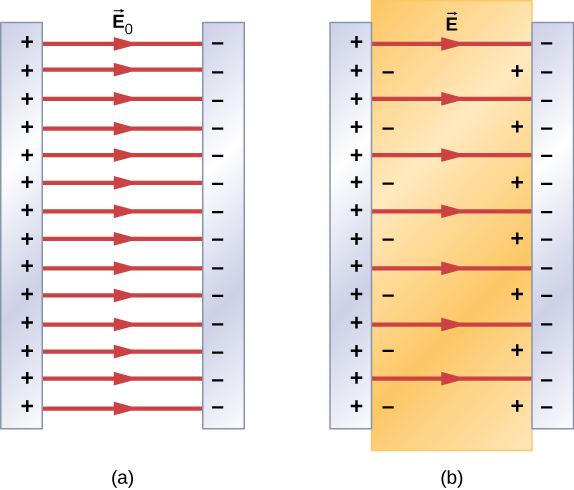
Therefore, when the region between the parallel plates of a charged capacitor, such as that shown in Figure \(\PageIndex{3a}\), is filled with a dielectric, within the dielectric there is an electrical field \(\vec{E}_0\) due to the free charge \(Q_0\) on the capacitor plates and an electrical field \(\vec{E}_i\) due to the induced charge \(Q_i\) on the surfaces of the dielectric. Their vector sum gives the net electrical field \(\vec{E}\) within the dielectric between the capacitor plates (shown in part (b) of the figure):

\[\vec{E} = \vec{E}_0 + \vec{E}_i. \label{eq1}\]

This net field can be considered to be the field produced by an effective charge \(Q_0 - Q_i\) on the capacitor.

Figure \(\PageIndex{3}\): Electrical field: (a) In an empty capacitor, electrical field \(\vec{E}_0\) (b) In a dielectric-filled capacitor, electrical field \(\vec{E}\).

In most dielectrics, the net electrical field \(\vec{E}\) is proportional to the field \(\vec{E}_0\) produced by the free charge. In terms of these two electrical fields, the dielectric constant \(\kappa\) of the material is defined as

\[\kappa = \dfrac{E_0}{E}. \label{eq2}\]

Since \(\vec{E}_0\) and \(\vec{E}_i\) point in opposite directions, the magnitude E is smaller than the magnitude \(\vec{E}_0\) and therefore \(\kappa > 1\). Combining Equations \ref{eq1} with \ref{eq2}, and rearranging the terms, yields the following expression for the induced electrical field in a dielectric:

\[\vec{E}_i = \left(\dfrac{1}{\kappa} - 1 \right) \vec{E}_0. \label{eq3}\]

When the magnitude of an external electrical field becomes too large, the molecules of dielectric material start to become ionized. A molecule or an atom is ionized when one or more electrons are removed from it and become free electrons, no longer bound to the molecular or atomic structure. When this happens, the material can conduct, thereby allowing charge to move through the dielectric from one capacitor plate to the other. This phenomenon is called dielectric breakdown. (Figure 8.1.1 shows typical random-path patterns of electrical discharge during dielectric breakdown.) The critical value, \(E_c\) of the electrical field at which the molecules of an insulator become ionized is called the dielectric strength of the material. The dielectric strength imposes a limit on the voltage that can be applied for a given plate separation in a capacitor. For example, the dielectric strength of air is \(E_c = 3.0 \, MV/m\), so for an air-filled capacitor with a plate separation of \(d = 1.00 \, mm\), the limit on the potential difference that can be safely applied across its plates without causing dielectric breakdown is \(V = E_c d = (3.0 \times 10^6 V/m)(1.00 \times 10^{-3} m) = 3.0 \, kV\).

However, this limit becomes 60.0 kV when the same capacitor is filled with Teflon™, whose dielectric strength is about \(60.0 \, MV/m\). Because of this limit imposed by the dielectric strength, the amount of charge that an air-filled capacitor can store is only \(Q_0 = \kappa_{air} C_0(3.0 \, kV)\) and the charge stored on the same Teflon™-filled capacitor can be as much as

\[\begin{align} Q &= \kappa_{teflon}C_0 (60.0 \, kV) \nonumber \\[4pt] &= \kappa_{teflon} \dfrac{Q_0}{\kappa_{air}(3.0 \, kV)} (60.0 \, kV) \nonumber \\[4pt] &= 20 \dfrac{\kappa_{teflon}}{\kappa_{air}}Q_0 = 20\dfrac{2.1}{1.00059}Q_0 \nonumber \\[4pt] &\cong 42 Q_0. \end{align} \]

which is about 42 times greater than a charge stored on an air-filled capacitor. Typical values of dielectric constants and dielectric strengths for various materials are given in Table \(\PageIndex{1}\). Notice that the dielectric constant \(\kappa\) is exactly 1.0 for a vacuum (the empty space serves as a reference condition) and very close to 1.0 for air under normal conditions (normal pressure at room temperature). These two values are so close that, in fact, the properties of an air-filled capacitor are essentially the same as those of an empty capacitor.

Table \(\PageIndex{1}\): Representative Values of Dielectric Constants and Dielectric Strengths of Various Materials at Room Temperature

Material	Dielectric constant \(\kappa\)	Dielectric strength \(E_c [\times 10^6 \, V/m]\)
Vacuum	1	\(\infty\)
Dry air (1 atm)	1.00059	3.0
Teflon™	2.1	60 to 173
Paraffin	2.3	11
Silicon oil	2.5	10 to 15
Polystyrene	2.56	19.7
Nylon	3.4	14
Paper	3.7	16
Fused quartz	3.78	8
Glass	4 to 6	9.8 to 13.8
Concrete	4.5	–
Bakelite	4.9	24
Diamond	5.5	2,000
Pyrex glass	5.6	14
Mica	6.0	118
Neoprene rubber	6.7	15.7 to 26.7
Water	80	-−
Sulfuric acid	84 to 100	-−
Titanium dioxide	86 to 173	–
Strontium titanate	310	8
Barium titanate	1,200 to 10,000	–
Calcium copper titanate	> 250,000	–

Not all substances listed in the table are good insulators, despite their high dielectric constants. Water, for example, consists of polar molecules and has a large dielectric constant of about 80. In a water molecule, electrons are more likely found around the oxygen nucleus than around the hydrogen nuclei. This makes the oxygen end of the molecule slightly negative and leaves the hydrogens end slightly positive, which makes the molecule easy to align along an external electrical field, and thus water has a large dielectric constant. However, the polar nature of water molecules also makes water a good solvent for many substances, which produces undesirable effects, because any concentration of free ions in water conducts electricity.

Example \(\PageIndex{1}\): Electrical Field and Induced Surface Charge

Suppose that the distance between the plates of the capacitor in Example 8.5.1 is 2.0 mm and the area of each plate is \(4.5 \times 10^{-3} m^2\). Determine:

1. the electrical field between the plates before and after the Teflon™ is inserted, and
2. the surface charge induced on the Teflon™ surfaces.

Strategy

In part (a), we know that the voltage across the empty capacitor is \(V_0 = 40 \, V\), so to find the electrical fields we use the relation \(V = Ed\) and Equation \ref{eq3}. In part (b), knowing the magnitude of the electrical field, we use the expression for the magnitude of electrical field near a charged plate \(E = \sigma/\epsilon_0\), where \(\sigma\) is a uniform surface charge density caused by the surface charge. We use the value of free charge \(Q_0 = 8.0 \times 10^{-10} C\) obtained in Example 8.5.1.

Solution

1. The electrical field \(E_0\) between the plates of an empty capacitor is \[E_0 = \dfrac{V_0}{d} = \dfrac{40 \, V}{2.0 \times 10^{-3} m} = 2.0 10^4 V/m. \nonumber\] The electrical field \(E\) with the Teflon™ in place is \[E = \dfrac{1}{\kappa}E_0 = \dfrac{1}{2.1}2.0 \times 10^4 V/m = 9.5 \times 10^3 \, V/m. \nonumber\]
2. The effective charge on the capacitor is the difference between the free charge \(Q_0\) and the induced charge \(Q_i\). The electrical field in the Teflon™ is caused by this effective charge. Thus \[\begin{align*} E &= \dfrac{1}{\epsilon_0}\sigma \\[4pt] &= \dfrac{1}{\epsilon_0} \dfrac{Q_0 - Q_i}{A}.\end{align*}\] We invert this equation to obtain \(Q_i\), which yields \[\begin{align*} Q_i &= Q_0 - \epsilon_0AE \\[4pt] &= 8.0 \times 10^{-10}C - \left(8.85 \times 10^{-12} \dfrac{C^2}{N \cdot m^2}\right)(4.5 \times 10^{-3}m^2)\left(9.5 \times 10^3 \, \dfrac{V}{m}\right) \\[4pt] &= 4.2 \times 10^{-10}C = 0.42 \, nC. \end{align*} \nonumber\]

Example \(\PageIndex{2}\): Inserting a Dielectric into a Capacitor Connected to a Battery

When a battery of voltage \(V_0\) is connected across an empty capacitor of capacitance \(C_0\), the charge on its plates is \(Q_0\), and the electrical field between its plates is \(E_0\). A dielectric of dielectric constant \(\kappa\) is inserted between the plates while the battery remains in place, as shown in Figure \(\PageIndex{4}\).

1. Find the capacitance \(C\), the voltage \(V\) across the capacitor, and the electrical field \(E\) between the plates after the dielectric is inserted.
2. Obtain an expression for the free charge \(Q\) on the plates of the filled capacitor and the induced charge \(Q_i\) on the dielectric surface in terms of the original plate charge \(Q_0\).

Figure \(\PageIndex{4}\): A dielectric is inserted into the charged capacitor while the capacitor remains connected to the battery.

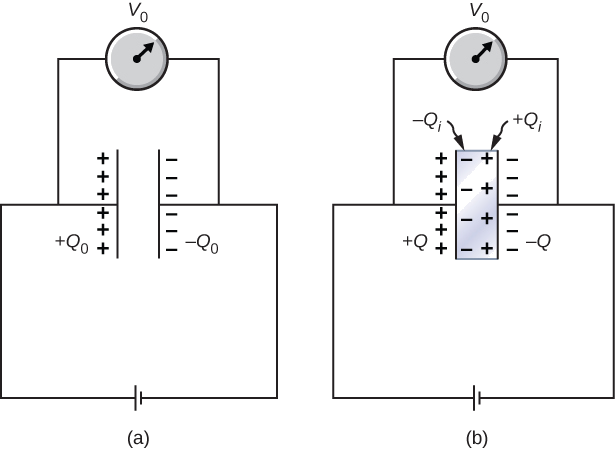
Strategy

We identify the known values:\(V_0, \, C_0, \, E_o, \, \kappa\), and \(Q_0\). Our task is to express the unknown values in terms of these known values.

Solution

(a) The capacitance of the filled capacitor is \(C = \kappa C_0\). Since the battery is always connected to the capacitor plates, the potential difference between them does not change; hence, \(V = V_0\). Because of that, the electrical field in the filled capacitor is the same as the field in the empty capacitor, so we can obtain directly that

\[E = \dfrac{V}{d} = \dfrac{V_0}{d} = E_0.\]

(b) For the filled capacitor, the free charge on the plates is

\[ \begin{align} Q &= CV \nonumber \\[4pt] &= (\kappa C_0)V_0 \nonumber \\[4pt] &= \kappa (C_0V_0) \nonumber \\[4pt] &= \kappa Q_0. \nonumber \end{align} \nonumber\]

The electrical field \(E\) in the filled capacitor is due to the effective charge \(Q - Q_i\) (Figure \(\PageIndex{4b}\)). Since \(E = E_0\), we have

\[\dfrac{Q - Q_i}{\epsilon_0 A} = \dfrac{Q_0}{\epsilon_0A}.\]

Solving this equation for \(Q_i\), we obtain for the induced charge

\[ \begin{align} Q_i &= Q - Q_0 \nonumber \\[4pt] &= \kappa Q_0 - Q_0 \nonumber \\[4pt] &= (\kappa -1)Q_0. \nonumber \end{align} \nonumber\]

Significance

Notice that for materials with dielectric constants larger than 2 (see Table \(\PageIndex{1}\)), the induced charge on the surface of dielectric is larger than the charge on the plates of a vacuum capacitor. The opposite is true for gasses like air whose dielectric constant is smaller than 2.

Exercise \(\PageIndex{1}\)

Continuing with Example \(\PageIndex{2}\), show that when the battery is connected across the plates the energy stored in dielectric-filled capacitor is \(U = \kappa U_0\) (larger than the energy \(U_0\) of an empty capacitor kept at the same voltage). Compare this result with the result \(U = U_0 /\kappa\) found previously for an isolated, charged capacitor.

Exercise \(\PageIndex{2}\)

Repeat the calculations of previous example for the case in which the battery remains connected while the dielectric is placed in the capacitor.

Answer

a. \(C_0 = 20 \, pF\), \(C = 42 \, pF\);

b. \(Q_0 = 0.8 \, nC\), \(Q = 1.7 \, nC\):

c. \(V_0 = V = 40 \, V\);

d. \(U_0 = 16 \, nJ\), \(U = 34 \, nJ\)