11.2: Magnetism and Its Historical Discoveries
- Page ID
- 4414
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Explain attraction and repulsion by magnets
- Describe the historical and contemporary applications of magnetism
Magnetism has been known since the time of the ancient Greeks, but it has always been a bit mysterious. You can see electricity in the flash of a lightning bolt, but when a compass needle points to magnetic north, you can’t see any force causing it to rotate. People learned about magnetic properties gradually, over many years, before several physicists of the nineteenth century connected magnetism with electricity. In this section, we review the basic ideas of magnetism and describe how they fit into the picture of a magnetic field.
Brief History of Magnetism
Magnets are commonly found in everyday objects, such as toys, hangers, elevators, doorbells, and computer devices. Experimentation on these magnets shows that all magnets have two poles: One is labeled north (N) and the other is labeled south (S). Magnetic poles repel if they are alike (both N or both S), they attract if they are opposite (one N and the other S), and both poles of a magnet attract unmagnetized pieces of iron. An important point to note here is that you cannot isolate an individual magnetic pole. Every piece of a magnet, no matter how small, which contains a north pole must also contain a south pole.
Visit this website for an interactive demonstration of magnetic north and south poles.
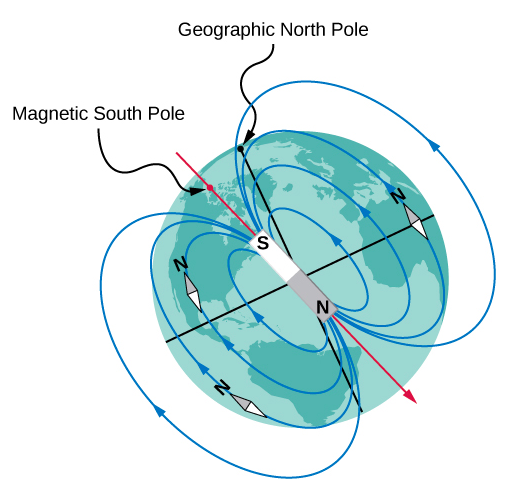
An example of a magnet is a compass needle. It is simply a thin bar magnet suspended at its center, so it is free to rotate in a horizontal plane. Earth itself also acts like a very large bar magnet, with its south-seeking pole near the geographic North Pole (Figure \(\PageIndex{1}\)). The north pole of a compass is attracted toward Earth’s geographic North Pole because the magnetic pole that is near the geographic North Pole is actually a south magnetic pole. Confusion arises because the geographic term “North Pole” has come to be used (incorrectly) for the magnetic pole that is near the North Pole. Thus, “north magnetic pole” is actually a misnomer—it should be called the south magnetic pole. [Note that the orientation of Earth’s magnetic field is not permanent but changes (“flips”) after long time intervals. Eventually, Earth’s north magnetic pole may be located near its geographic North Pole.]
Back in 1819, the Danish physicist Hans Oersted was performing a lecture demonstration for some students and noticed that a compass needle moved whenever current flowed in a nearby wire. Further investigation of this phenomenon convinced Oersted that an electric current could somehow cause a magnetic force. He reported this finding to an 1820 meeting of the French Academy of Science.
Soon after this report, Oersted’s investigations were repeated and expanded upon by other scientists. Among those whose work was especially important were Jean-Baptiste Biot and Felix Savart, who investigated the forces exerted on magnets by currents; André Marie Ampère, who studied the forces exerted by one current on another; François Arago, who found that iron could be magnetized by a current; and Humphry Davy, who discovered that a magnet exerts a force on a wire carrying an electric current. Within 10 years of Oersted’s discovery, Michael Faraday found that the relative motion of a magnet and a metallic wire induced current in the wire. This finding showed not only that a current has a magnetic effect, but that a magnet can generate electric current. You will see later that the names of Biot, Savart, Ampère, and Faraday are linked to some of the fundamental laws of electromagnetism.
The evidence from these various experiments led Ampère to propose that electric current is the source of all magnetic phenomena. To explain permanent magnets, he suggested that matter contains microscopic current loops that are somehow aligned when a material is magnetized. Today, we know that permanent magnets are actually created by the alignment of spinning electrons, a situation quite similar to that proposed by Ampère. This model of permanent magnets was developed by Ampère almost a century before the atomic nature of matter was understood. (For a full quantum mechanical treatment of magnetic spins, see Quantum Mechanics and Atomic Structure.)
Contemporary Applications of Magnetism
Today, magnetism plays many important roles in our lives. Physicists’ understanding of magnetism has enabled the development of technologies that affect both individuals and society. The electronic tablet in your purse or backpack, for example, wouldn’t have been possible without the applications of magnetism and electricity on a small scale (Figure \(\PageIndex{2}\)). Weak changes in a magnetic field in a thin film of iron and chromium were discovered to bring about much larger changes in resistance, called giant magnetoresistance. Information can then be recorded magnetically based on the direction in which the iron layer is magnetized. As a result of the discovery of giant magnetoresistance and its applications to digital storage, the 2007 Nobel Prize in Physics was awarded to Albert Fert from France and Peter Grunberg from Germany.

All electric motors—with uses as diverse as powering refrigerators, starting cars, and moving elevators—contain magnets. Generators, whether producing hydroelectric power or running bicycle lights, use magnetic fields. Recycling facilities employ magnets to separate iron from other refuse. Research into using magnetic containment of fusion as a future energy source has been continuing for several years. Magnetic resonance imaging (MRI) has become an important diagnostic tool in the field of medicine, and the use of magnetism to explore brain activity is a subject of contemporary research and development. The list of applications also includes computer hard drives, tape recording, detection of inhaled asbestos, and levitation of high-speed trains. Magnetism is involved in the structure of atomic energy levels, as well as the motion of cosmic rays and charged particles trapped in the Van Allen belts around Earth. Once again, we see that all these disparate phenomena are linked by a small number of underlying physical principles.


