5.8: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise \PageIndex{1}
A particle is in a region where the potential energy has the form U = 5/x (in joules, if x is in meters).
- Sketch this potential energy function for x > 0.
- Assuming the particle starts at rest at x = 0.5 m, which way will it go if released? Why?
- Under the assumption in part (b), what will be the particle’s kinetic energy after it has moved 0.1 m from its original position?
- Now assume that initially the particle is at x = 1 m, moving towards the left with an initial velocity v_i = 2 m/s. If the mass of the particle is 1 kg, how close to the origin can it get before it stops?
Exercise \PageIndex{2}
A “ballistic pendulum” is a device (now largely obsolete, but very useful in its day) to measure the speed of a bullet as it hits a target. Let the target be a block of wood suspended from a string, as in the figure below. When the bullet hits, it is embedded in the wood, and together they swing, like a pendulum, to some maximum height h. The question is, how do you find the initial speed of the bullet (v_i) if you know the mass of the bullet (m_1), the mass of the block (m_2), and the height h?
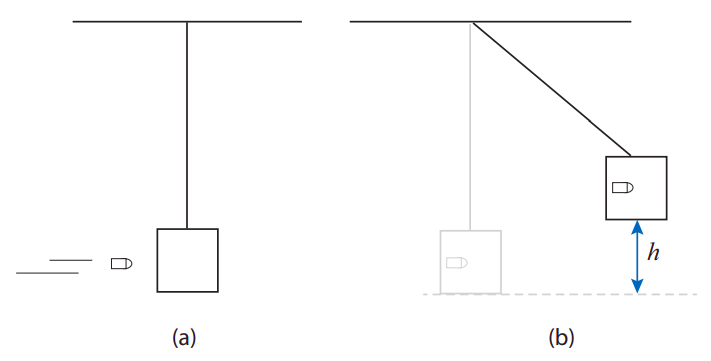
Figure \PageIndex{1}: Ballistic pendulum. (a) Before the bullet hits. (b) After the bullet hits and is embedded in the block, at the maximum height of the swing.
Exercise \PageIndex{3}
You drop a 0.5 kg ball from a height of 2 m, and it bounces back to a height of 1.5 m. Consider the system formed by the ball and the Earth, so we can speak properly of its gravitational potential energy.
- What is the kinetic energy of the ball just before it hits the ground?
- What is the kinetic energy of the ball just after it bounces up?
- What is the coefficient of restitution for this collision?
- What kind of collision is this (elastic, inelastic, etc.)? Why?
- If the coefficient of restitution does not change, how high would the ball rise on a second bounce?
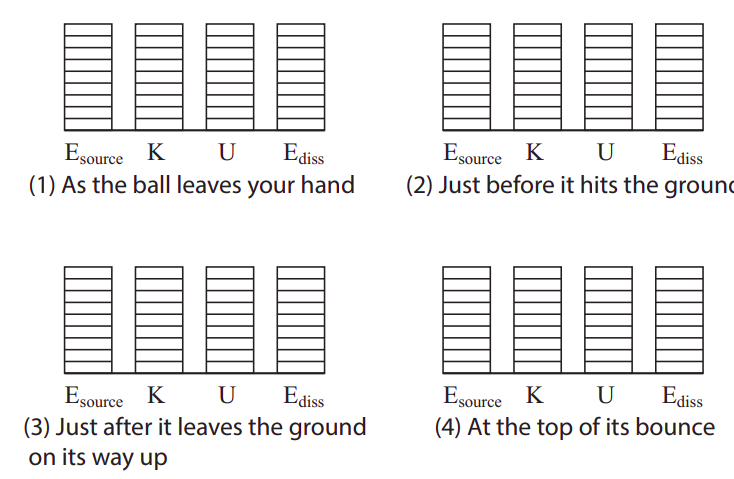
- On the graphs below, draw the energy bar diagrams for the system: (1) as the ball leaves your hand; (2) just before it hits the ground (assume h = 0 for practical purposes); (3) just after it leaves the ground on its way up (h = 0 still), and (4) at the top of its (first) bounce. Make sure to do this to scale, consistent with the values for the energies you have calculated above.
Exercise \PageIndex{4}
A 60-kg skydiver jumps from an airplane 4000 m above the earth. After falling 450 m, he reaches a terminal speed of 55 m/s (about 120 mph). This means that after this time his speed does not increase any more.
- At the moment of the jump, what is the initial (gravitational) potential energy of the system formed by the earth and the skydiver? (Take U^G = 0 at ground level.)
- After the skydiver has fallen 450 m, what is the (gravitational) potential energy of the system? (Call this the “final” potential energy.)
- What is the final kinetic energy of the diver at that time?
- Assume the initial kinetic energy of the skydiver is zero. Is \Delta K = −\Delta U for this system? If not, explain what happened to the “missing” energy.
- Can the skydiver and the earth below (excluding the atmosphere!) be considered a closed system here? Explain.
- After the skydiver reaches terminal speed (and before he opens his parachute), he falls for a while at constant speed. What kind of energy conversion is taking place during this time? (Consider the system to be the earth, the skydiver, and the air around him).
Exercise \PageIndex{5}
You shoot a 1-kg projectile straight up from a spring toy gun, and find that it reaches a height of 5 m. (How do you figure out the height? From the time of flight, of course! See Exercise 2.6.2 from Chapter 2.) You also measure that when you load the gun, the spring compresses a distance 10 cm. What is the value of the spring constant?


