7.2: Work on a Single Particle
( \newcommand{\kernel}{\mathrm{null}\,}\)
Consider a particle that undergoes a displacement Δx while a constant force F acts on it. In one dimension, the work done by the force on the particle is defined by
W = F \Delta x \quad (\mathrm{constant \: force}) \label{eq:7.4}
and it is positive if the force and the displacement have the same sign (that is, if they point in the same direction), and negative otherwise.
In three dimensions, the force will be a vector \vec F with components (F_x, F_y, F_z), and the displacement, likewise, will be a vector \Delta \vec r with components (\Delta x, \Delta y, \Delta z). The work will be defined then as
W=F_{x} \Delta x+F_{y} \Delta y+F_{z} \Delta z \label{eq:7.5} .
This expression is an instance of what is known as the dot product (or inner product, or scalar product) of two vectors. Given two vectors \vec A and \vec B , their dot product is defined, in terms of their components,
\vec{A} \cdot \vec{B}=A_{x} B_{x}+A_{y} B_{y}+A_{z} B_{z} \label{eq:7.6} .
This can also be expressed in terms of the vectors’ magnitudes, |\vec A| and |\vec B|, and the angle they make, in the following form:
\vec{A} \cdot \vec{B}=|\vec{A}||\vec{B}| \cos \phi \label{eq:7.7}
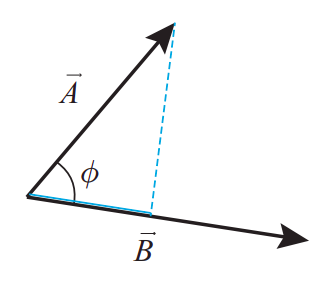
Figure \PageIndex{1} shows what I mean by the angle \phi in this expression. The equality of the two definitions, Eqs. (\ref{eq:7.6}) and (\ref{eq:7.7}), is proved in mathematics textbooks. The advantage of Equation (\ref{eq:7.7}) is that it is independent of the choice of a system of coordinates.
Using the dot product notation, the work done by a constant force can be written as
W=\vec{F} \cdot \Delta \vec{r} \label{eq:7.8} .
Equation (\ref{eq:7.7}) then shows that, as I mentioned in the introduction, when the force is perpendicular to the displacement (\phi = 90^{\circ}) the work it does is zero. You can also see this directly from Equation (\ref{eq:7.5}), by choosing the x axis to point in the direction of the force (so F_y = F_z = 0), and the displacement to point along any of the other two axes (so \Delta x = 0): the result is W = 0.
If the force is not constant, again we follow the standard procedure of breaking up the total displacement into pieces that are short enough that the force may be taken to be constant over each of them, calculating all those (possibly very small) “pieces of work,” and adding them all together. In one dimension, the final result can be expressed as the integral
W=\int_{x_{i}}^{x_{f}} F(x) d x \quad(\text { variable force }) \label{eq:7.9} .
So the work is given by the “area” under the F-vs-x curve. In more dimensions, we have to write a kind of multivariable integral known as a line integral. That is advanced calculus, so we will not go there this semester.
Work Done by the Net Force, and the Work-Energy Theorem
So much for the math and the definitions. Where does the energy come in? Let us suppose that F is either the only force or the net force on the particle—the sum of all the forces acting on the particle. Again, for simplicity we will assume that it is constant (does not change) while the particle undergoes the displacement \Delta x. However, now \Delta x and F_{net} are related: a constant net force means a constant acceleration, a = F_{net}/m, and for constant acceleration we know the formula v^2_f − v^2_i = 2a \Delta x applies. Therefore, we can write
W_{n e t}=F_{n e t} \Delta x=m a \Delta x=m \frac{1}{2}\left(v_{f}^{2}-v_{i}^{2}\right) \label{eq:7.10}
which is to say
W_{n e t}=\Delta K \label{eq:7.11} .
In words, the work done by the net force acting on a particle as it moves equals the change in the particle’s kinetic energy in the course of its displacement. This result is often referred to as the Work-Energy Theorem.
As you may have guessed from our calling it a “theorem,” the result (\ref{eq:7.11}) is very general. It holds in three dimensions, and it holds also when the force isn’t constant throughout the displacement— you just have to use the correct equation to calculate the work in those cases. It would apply to the work done by the net force on an extended object, also, provided it is OK to treat the extended object as a particle—so basically, a rigid object that is moving as a whole and not doing anything fancy such as spinning while doing so.
Another possible direction in which to generalize (\ref{eq:7.11}) might be as follows. By definition, a “particle” has no other kind of energy, besides (translational) kinetic energy. Also, and for the same reason (namely, the absence of internal structure), it has no “internal” forces—all the forces acting on it are external. So—for this very simple system—we could rephrase the result (\ref{eq:7.11}) by saying that the work done by the net external force acting on the system (the particle in this case) is equal to the change in its total energy. It is in fact in this form that we will ultimately generalize (\ref{eq:7.11}) to deal with arbitrary systems.
Before we go there, however, I would like to take a little detour to explore another “reasonable” extension of the result (\ref{eq:7.11}), as well as its limitations.


