9.9: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 9.9.1
An ice skater has a moment of inertia equal to 1.9 kg·m2 when she is rotating with her arms stretched out, at a rate of 2 revolutions per second. She then brings her arms in, lined up with her axis of rotation, so her moment of inertia becomes 1.1 kg·m2.
- What is her new angular velocity? (You may use radians per second, or revolutions per second if you prefer.)
- What is the change in her kinetic energy?
- Where did this energy come from?
Exercise 9.9.2
Two identical pucks, each of inertia m, are connected to a rod of length 2r and negligible inertia that is pivoted about its center (that is, there is some sort of pin though its center, around which it can rotate without friction). A third puck of inertia m/2 strikes one of the connected pucks perpendicular to the rod with a speed vi. Assume the collision is elastic.
- Draw a diagram of the situation, clearly labeling the direction of vi and what direction the connected pucks will rotate.
- Is the total momentum of the system (the three pucks and the rod) conserved throughout the interaction? Why? Is the system isolated, or can you identify an external force acting on it?
- Is the total kinetic energy of the system conserved? Why? If you found an external force in part (b), explain why it does or does not do work on the system.
- Is the total angular momentum of the system conserved? Why? If you found an external force in part (b), explain why it does or does not exert a torque on the system.
- Write down an expression for the moment of inertia (rotational inertia) of the system formed by the connected pucks.
- Based on all of the above, write down equations expressing the conservation of the two quantities that are in fact conserved. These equations should involve only the given data (masses, length of rod); the initial and final velocities, vi and vf , of the free puck; and ω, the angular speed of the connected pucks after the collision. (Assume the final velocity of the free puck lies along the same line as its initial velocity, that is, it does not bounce off at some random angle.)
Exercise 9.9.3
A plank of length l = 2 m is hinged at one end to a wall. The other end is being (temporarily) supported by a worker who is holding it up with his hand, keeping the plank horizontal. The plank has a mass of 20 kg, and there is also a toolbox of mass 5 kg sitting on it, 50 cm away from the worker (1.5 m away from the wall).
- Draw a free body diagram and an extended free-body diagram for the plank.
- What are the magnitudes of (1) the upwards force exerted by the worker on the plank and (2) the force at the hinge?
- If the worker were to let go of the plank, what would its angular acceleration be as it starts swinging down? The moment of inertia is I=13Ml2. (Note: assume the toolbox stops pressing down on the plank immediately. This is a good approximation, as you shall see below.)
- Consider a point on the plank located immediately below the toolbox. As the plank swings, this point moves in a circle of radius 1.5 m. What is its linear (tangential) acceleration as it starts going down, and how does it compare to the acceleration of gravity?
Exercise 9.9.4
A solid sphere of radius 5 cm and mass 0.2 kg is rolling without slipping, on level ground, at a constant speed of 0.5 m/s. It is heading toward a ramp that makes an angle of 30∘ with the horizontal.
- What is the angular velocity of the sphere, in radians per second?
- If the moment of inertia of a solid, homogeneous sphere is I=25mR2, what is the initial angular momentum of this sphere?
- What is the translational kinetic energy of the sphere?
- What is its rotational kinetic energy?
- How high (vertically) will the sphere rise as it goes up the ramp, still rolling without slipping, before it stops and turns around?
- Draw an extended free-body diagram for the sphere as it rolls up the ramp. On the diagram, indicate the direction of rotation, and the direction of the acceleration of the center of mass.
- Referring to the extended free-body diagram in the previous question, which force is responsible for the change in the angular momentum of the sphere as it rolls up the ramp? Explain briefly: Why that force and not another one? Does the direction you have assumed for this force agree with the torque it has to provide? (If not, you’d better go back and fix that right now!)
- Calculate the acceleration of the sphere as it rolls up the ramp.
Exercise 9.9.5
A very light, inextensible string is wrapped around a cylindrical spool. The end of the string is held fixed, and the spool is released so it starts falling, as the string unwinds. Because the spool is basically hollow, you can take its moment of inertia to be I=mR2.
- Draw an extended free-body diagram for the spool as it unrolls.
- Find the linear acceleration of the spool as it accelerates toward the ground.
- Let the mass of the spool be 0.1 kg. What is its translational kinetic energy after it has fallen for 0.5 s?
- What is its rotational kinetic energy at that time?
- What is the tension in the string? Does this change as the spool falls? (Remember the mass of the string is negligible.)
- If the radius of the spool is 3 cm, what is the magnitude of the torque (around the center of mass) exerted by the tension?
Exercise 9.9.6
A 20 kg plank of length l = 4 m is supported at both ends as shown in the figure. A 60 kg man is standing a distance l/3 from the right end of the plank.
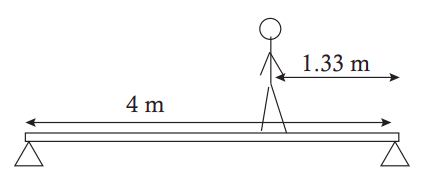
- Draw an extended free-body diagram for the plank. Try to get the scale of the forces at least qualitatively right.
- Find the upwards force on the plank exerted by each of the two supports.


