12.7: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Exercise 12.7.1
When plucked, the D string on a guitar vibrates with a frequency of 147 Hz.
- What would happen to this frequency if you were to increase the tension in the string?
- The vibration of the string eventually produces a sound wave of the same frequency, traveling through the air. If the speed of sound in air is 340 m/s, what is the wavelength of this wave?
Exercise 12.7.2
Think of a flute as basically a cylindrical tube of length 0.6 m, open to the atmosphere at both ends. If the speed of sound in air is 340 m/s
- What is the fundamental (lowest) frequency of a sound wave in a flute?
- Is this a transverse or a longitudinal wave?
- The speed of sound in helium is about 3 times that in air. How would the flute’s resonance frequencies change if you filled it with helium instead of air?
Justify each of your answers briefly.
Exercise 12.7.3
The top picture shows a wave pulse on a string (string 1) traveling to the right, where the string is attached to another one (string 2, not shown). The bottom picture shows the reflected wave some time later.
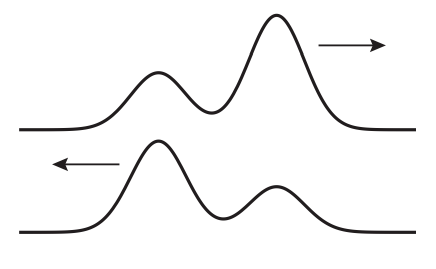
If the tension on both strings is the same,
- Is string 2 more or less dense than string 1?
- In which string will the wave travel faster?
- Sketch what the reflected wave would look like if the strings’ densities were the opposite of what you answered in part (a).
Explain each of your answers briefly.


