8.2: Force, Power and Impedance

Whatever is enforcing the boundary conditions in the example of (8.9) must exert a force on the string. Of course, a horizontal force is required to keep the string stretched, but for small oscillations, this force is nearly constant and approximately equal to the string tension, \(T\). Furthermore, there is no motion in the \(x\) direction so no work is done by this component of the force. The vertical component of the force is the negative of the force which the tension on the string produces. At \(x = 0\), this is \[F_{0}=-\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=0} .\]

This is illustrated in \(Figure \text { } 8.5\).

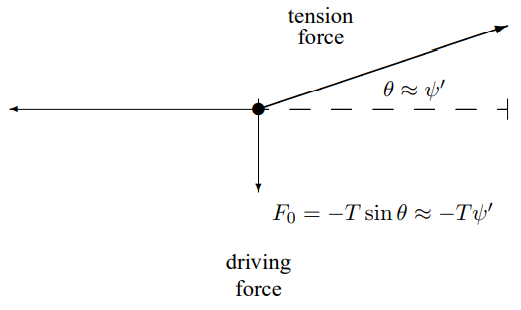
Figure \( 8.5\): The force due to a string pulling in the \(+ x\) direction.

At \(x = L\), because the string is coming in from the \(- x\) direction, it is \[F_{L}=\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=L} ,\]

as illustrated in the Figure \( 8.6\).

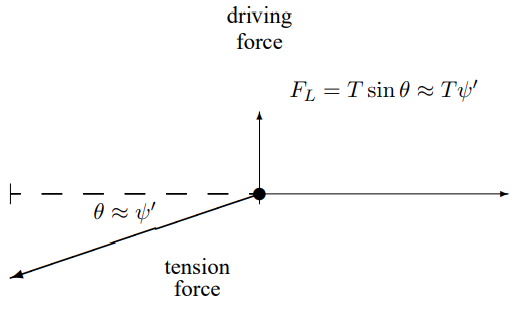
Figure \( 8.6\): The force due to a string pulling in the \(- x\) direction.

In the forced oscillation, the end of the string is moving only in the transverse direction. Thus the power supplied by the external force at \(x = 0\), which is \(\vec{F} \cdot \vec{v}\) is \[P(t)=-\left.T \frac{\partial}{\partial x} \psi(x, t)\right|_{x=0} \frac{\partial}{\partial t} \psi(0, t)\]

where as in (2.26), \(\psi(x,t)\) is the real displacement from equilibrium for the piece of string at horizontal position \(x\). We must take the real part first because the power is a nonlinear function of the displacement.

For a standing wave on the string (or any system with no frictional forces), the force and the velocity are \(90^{\circ}\) out of phase. For example, if the displacement is proportional to \(\sin \omega t\), then the transverse force at each end is also proportional to \(\sin \omega t\). The velocity, however, is proportional to \(\cos \omega t\). Thus the power expended by the external force is \[\propto \sin \omega t \cos \omega t=\frac{1}{2} \sin 2 \omega t .\]

This averages to zero over a half-cycle. On the average, no power is required to keep the standing wave going (in the absence of damping).

In a traveling wave, on the other hand, the force and the velocity are proportional. From (8.15), you can see that \[\propto \sin \omega t \cos \omega t=\frac{1}{2} \sin 2 \omega t\]

Thus \[F_{0}=Z \frac{\partial}{\partial t} \psi(0, t), \quad F_{L}=-Z \frac{\partial}{\partial t} \psi(L, t) ,\]

where the constant \(Z\), \[Z=\frac{T k}{\omega}=\sqrt{\rho T} ,\]

is called the “impedance” of the string system. It measures the power required to produce the traveling wave. The power required at \(x = 0\) is \[P_{0}=Z\left(\frac{\partial}{\partial t} \psi(0, t)\right)^{2}=Z A^{2} \omega^{2} \sin ^{2} \omega t .\]

The average power expended is thus \[\left\langle P_{0}\right\rangle=Z A^{2} \omega^{2} / 2 .\]

The power expended at \(x = 0\) to produce the traveling wave is given up by the string at \(x = L\), because the power required at \(L\) is \[P_{L}=-Z\left(\frac{\partial}{\partial t} \psi(L, t)\right)^{2}=-Z A^{2} \omega^{2} \cos ^{2} \omega t .\]

If the boundary conditions were such that the traveling waves were going in the opposite direction, the force in the above derivations would have the opposite sign from (8.20). Thus the positive power is always required to produce the wave and the negative power is required to absorb it. It may seem odd that the power fed into the wave in (8.23) and the power given up by the wave in (8.25) are not exactly equal and opposite. The sum vanishes on the average, but oscillates with time. The reason is that the length of the system is not an integral number of wavelengths. This allows the energy stored on the system, the sum of kinetic and potential, to oscillate as a function of time.

Note that the force required to absorb a traveling wave, in (8.21), is negative and proportional to the velocity. This is a typical frictional force. Thus a traveling wave can be absorbed completely by a frictional force (or a resistance) with exactly the right ratio of force to velocity. If the impedance of the “dashpot” (as such a resistance is called) is not exactly the same as that of the string, there will be some reflection. We will come back to this in the next chapter.

Complex Impedance

For the stretched string, a system for which the dispersion relation is equivalent to the wave equation, (6.4), the force on the system and the displacement velocity, \(\frac{\partial}{\partial t} \psi\), are proportional for any traveling wave.¹ In general, this is not true. For example, consider the beaded string of Figure \( 5.4\) stretched from \(x = 0\) to some large \(x\). Suppose further that there is a traveling wave in the system of the form, \[\psi(x, t)=A \cos (k x-\omega t) ,\]

illustrated in Figure \( 8.7\).² The dotted line is the equilibrium position of the string.

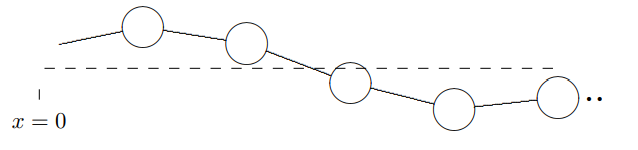
Figure \( 8.7\): A snapshot of a traveling wave in a beaded string.

So long as \(k\) and \(\omega\) are related by the dispersion relation, (5.39), then (8.26) is a solution to the equation of motion. The external transverse force at \(x = 0\) required to produce the traveling wave is related to the difference between the displacement of the first block and the displacement of the end at \(x = 0\) (see figure 5.5). It is \[F_{0}=\frac{T A}{a}(\cos (\omega t-k a)-\cos \omega t) .\]

This is approximately proportional to the velocity only if \(ka\) is very small, so that the right-hand side of (8.27) can be expanded in a Taylor series. Thus in this case, and in general for a discrete system, we cannot define the impedance simply as in (8.21).

However, suppose that instead of the real traveling waves, (8.26), we consider a complex harmonic traveling wave with irreducible time and space of the form \[\psi(x, t)=A e^{-i(\omega t-k x)} .\]

Then because of the irreducible on \(t\) and \(x\) (that comes from translation invariance), we know immediately that the both the force and the \(t\) derivative of \(\psi\) are proportional to \(\psi\). For an irreducible solution, everything is proportional to \(e^{-i(\omega t-k x)}\). Thus they are also proportional to each other, and we can define the impedance, \[F=-Z(k) \frac{\partial}{\partial t} \psi(x, t)=i \omega A Z(k) e^{-i(\omega t-k x)} .\]

For example, for the beaded string, if we replace the real solution, (8.26), with the irreducible complex solution, (8.28), the force becomes \[F_{0}=\frac{T A}{a}\left(e^{-i(\omega t-k a)}-e^{-i \omega t}\right)=\frac{T A}{a}\left(e^{i k a}-1\right) e^{-i \omega t} .\]

Thus from (8.29), the impedance, \(Z(k)\), is \[Z(k)=\frac{T}{\omega a} \frac{e^{i k a}-1}{i}=\frac{2 T}{a} e^{i k a / 2} \frac{\sin \frac{k a}{2}}{\omega} .\]

Using the dispersion relation, (5.39), we can write this as \[Z(k)=e^{i k a / 2} \sqrt{\frac{m T}{a}} .\]

The impedance, \(Z(k)\), defined by (8.29) is, in general, complex, and \(k\) dependent. Nevertheless, we can find the average power required to produce the wave. Because the power is a nonlinear function of the displacement, we must first take the real parts of the complex velocity and complex force before computing the power, as in (2.26). For arbitrary complex \(A=|A| e^{i \phi}\), \[\begin{gathered}
v=\omega|A| \sin (\omega t-k x-\phi) , \\
F=(\operatorname{Im} Z(k)) \omega|A| \cos (\omega t-k x-\phi)+(\operatorname{Re} Z(k)) \omega|A| \sin (\omega t-k x-\phi),
\end{gathered}\]

where we have put the phase of \(A\) into the \(\cos\) and \(\sin\) functions (see (1.96)-(1.98)) to make it clear that only the absolute value of \(A\) matters for the average power. Then, as in (2.26), only the \(\sin^{2}\) term contributes to the time-averaged power, which is \[\frac{1}{2}(\operatorname{Re} Z) \omega^{2}|A|^{2} .\]

______________________
¹We will see this in detail in chapter 10.
²For an animation of a traveling wave in a similar system, see program 8-6. The system shown in this program has the beads on springs, as well as on a string. However, the form of the traveling wave is the same. Only the dispersion relation is different.