12.3: Wave Plates and Polarizers
( \newcommand{\kernel}{\mathrm{null}\,}\)
One reason that polarization is important is that the polarization state of an electromagnetic wave can be easily manipulated. Two of the most important devices for such manipulation are polarizers and wave plates.
Unpolarized Light
 12-2
12-2
In any beam of light, at any given point and time, the electric field points in a particular direction. Likewise, because any plane electromagnetic wave with a definite angular frequency can be described by (12.20) and (12.21), →E=Re(→e(→k)ei→k⋅→r−iωt)→B=Re(→b(→k)ei→k⋅→r−iωt)
→b(→k)=1ω→k×→e(→k)=ncˆk×→e(→k) and ˆk⋅→e(→k)=0.
every plane wave is polarized. However, in an “unpolarized” beam, the light wave consists of a range of angular frequencies with different polarizations. As a result of the interference of the different harmonic components of the wave, the polarization wanders more or less randomly as a function of time and space, and on the average, no particular polarization is picked out. A simple example of what this looks like is animated in program 12-2, where we plot an electric field of the form Ex(t)=cos(ω1t+ϕ1)+cos(ω2t+ϕ2),Ey(t)=cos(ω3t+ϕ3)+cos(ω4t+ϕ4),
where the phases are random and the frequencies are chosen at random in a small range around a central frequency. You can watch the →E field wandering in the x-y plane, eventually filling it up. The narrower the range of frequencies in the wave, the more slowly the polarization wanders. In the example in program 12-2, the range of frequencies is of the order of 10% of the central frequency, so the polarization wanders rapidly. But for a beam with a fairly well-defined frequency, the polarization will be nearly constant over many cycles of the wave. The time over which the polarization is approximately constant is called the coherence time of the wave. For a plane wave of definite frequency, the coherence time is infinite.
Polarizers
A “polarizer” is a device that allows light polarized in a particular direction (the “easy transmission axis” of the polarizer) to pass through with very little absorption, but absorbs most of the light polarized in the perpendicular direction. Thus an unpolarized light beam, passing though the polarizer, emerges polarized along the easy axis.
For the transverse oscillations of a string, a polarizer is simply a slit that allows the string to oscillate in one transverse direction but not in the perpendicular direction.
For electromagnetic waves, the most familiar example of a polarizer, Polaroid, was invented by Edwin Land over 50 years ago, partly in experiments done in the attic of the Jefferson Physical Laboratory, where he worked as an undergraduate at Harvard. The idea of polaroid is to make material that conducts electricity (poorly) in one direction, but not in the other. Then the electric field in the conducting direction will be absorbed (the energy going to resistive loss), while the electric field in the nonconductive direction will be unaffected. One way of doing this is to make sheets of polymer (polyvinyl alcohol) stretched (to align the polymer molecules along a preferred axis) and doped with iodine (to allow conduction along the polymer molecules).2
Wave Plates
“Wave plates” are optical elements that change the relative phase of the two components of Z. Wave plates are possible because there are materials in which the index of refraction depends on the polarization. This property is called “birefringence.” It can happen in various ways.
For example, the transparent polymer material cellophane is made into thin sheets by stretching. Because of the stretching, the polymer strands tend to be oriented along the stretch direction. The dielectric constant in this material depends on the direction of the electric field. It is easier for charges to move along the polymer strands than across them. Thus the dielectric constant is larger for electric fields in the stretch direction.
The same effect may arise because of the inherent structure of a transparent crystal. An example is the naturally occurring mineral, calcite, a crystalline form of calcium carbonate, CaCO3. Crystals of calcite have the fascinating property of splitting a beam of unpolarized light into its two polarization states. Birefringence can even be produced mechanically, by stressing a transparent material, squeezing the electronic structure in one direction.
However the birefringence is produced, we can make a wave plate by orienting the material so that the x and y directions correspond to different indices of refraction, nx and ny, and then making a slice of the material in the form of a plate in the x-y plane, with some thickness ℓ in the z direction. Now an electromagnetic wave traveling in the z direction through the plate has different k values depending on its polarization: k={nxcω for polarization in the x direction nycω for polarization in the y direction
In particular, the phase difference, between x and y polarized light in going through the plate is Δϕ=nx−nycωℓ.
Note that in general the phase difference, Δϕ, depends on the frequency of the light. Even if nx and ny depend on frequency, it would be a bizarre accident if that dependence canceled the ω dependence from the explicit factor of ω in (12.39).
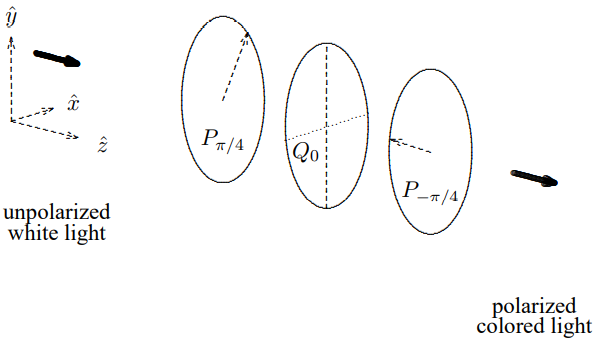
Figure 12.5: Initially unpolarized light passing through a pair of crossed polarizers with a wave plate in between.
Consider, now, putting such a wave plate between two crossed polarizers, oriented at ±45∘, as shown in Figure 12.5. Without the wave plate, no light would get through because the first polarizer transmits only light polarized at 45∘, described by the Z vector Z=(1/√21/√2)
and the second polarizer absorbs it.
Coming out of the first polarizer, the vector, Z, looks like (12.40) for all the frequency components in the white light. But when the wave plate is inserted in between, a frequency dependent phase difference is added, so that the Z vector coming out of the wave plate (up to an irrelevant overall phase) looks like Z=(1/√2e−iΔϕ/√2).
For frequencies such that e−iΔϕ is −1, the light is polarized in the −45∘ direction, and gets e−iΔϕ through the second polarizer without further attenuation. But for frequencies such that e is 1, the light is still absorbed by the second polarizer. Intermediate frequencies are partially absorbed.
It is this frequency dependence that produces the interesting patterns of color that you see when you put cellophane or a stressed piece of plastic between polarizers.
Matrices
The effects of wave plates and polarizers and the like can be summarized by multiplication of the Z vector by 2×2 matrices. For example, a perfect polarizer with an axis at an angle θ from the 1 axis can be represented by Pθ=(cos2θcosθsinθcosθsinθsin2θ).
The object Pθ is called a “projection operator,” because it projects the vector onto the direction parallel to uθ. It satisfies PθPθ=Pθ,
as it must, since the first polarizer produces polarized light and the second one transmits it perfectly. Pθ acting on a vector transmits the component in the θ direction. This is easiest to visualize if θ=0 or π/2. The matrices P0=(1000),Pπ/2=(0001),
represent polarizers along the 1 and 2 axes respectively.
A wave plate in which the phase difference is π/2 is called a “quarter wave plate.” For a wave plate in which the phase difference is between 0 and π, it is conventional to call the axis with the smaller phase the “fast axis.” A quarter wave plate with fast axis along the 1 axis is represented by Q0=(100i).
Notice that we can write Q0=P0+iPπ/2.
This should convince you that in general if the fast axis is in the θ direction, the quarter wave plate looks like Qθ=Pθ+iPθ+π/2.
The discussion of (12.39) shows that in general, a wave plate will only be a quarter wave plate for light of a definite frequency.
A wave plate in which the phase difference is π is called a “half wave plate.” A half wave plate is obtained by replacing the i in (12.45)-(12.47) by -1. Thus, Hθ=Pθ−Pθ+π/2.
Notice that Hθ=QθQθ;
two quarter wave plates make a half wave plate.
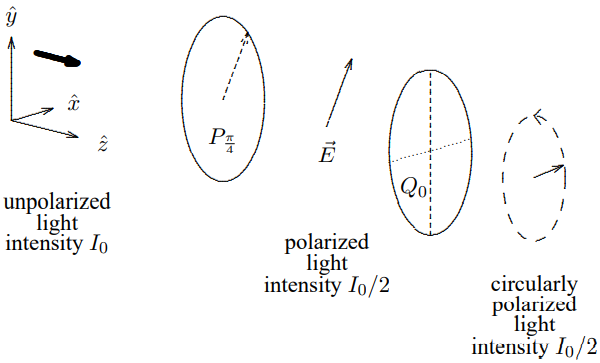
Figure 12.6: Producing circularly polarized light.
Here are two amusing devices that you can make with these optical elements (or matrices). Consider the combination of first a polarizer at 45∘ and then a quarter wave plate, as shown in Figure 12.6. By forming the matrix product, Q0Pπ/4, you can see that this produces counterclockwise circularly polarized light from anything with a component of polarization in the π/4 direction. The argument goes like this. The product is Q0Pπ/4=(100i)(1/21/21/21/2)=(1/21/2i/2i/2).
When this acts on an arbitrary vector you get circularly polarization unless the vector is annihilated by Pπ/4. Q0Pπ/4(ψ1ψ2)=ψ1+ψ22(1i).
In the opposite order, Pπ/4Q0 is an analyzer for circularly polarized light. It annihilates counterclockwise light and converts clockwise polarized light to light linearly polarized in the π/4 direction.
Optical Activity
“Optical activity” is a property of many organic and some inorganic compounds. An optically active material rotates the polarization of light without absorbing either component of the polarization. A familiar example of such a material is corn syrup, a thick aqueous solution of sugar that you probably have in your kitchen. If you put a rectangular container of corn syrup between polarizers, as shown in Figure 12.7, and rotate the second polarizer until the intensity of the light getting through is a maximum, you will find that direction of the second polarizer is not the same as that of the first. The plane of the polarization has been rotated by some angle θ. The rotation angle, θ, is proportional to the thickness of the container, the length of the region of syrup that the light goes through.
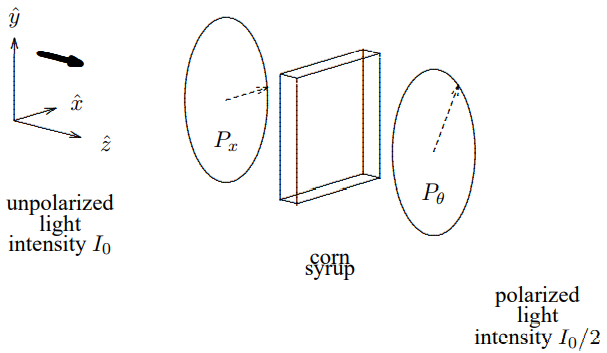
Figure 12.7: A rectangular container of corn syrup between polarizers.
Clearly, the optical activity of corn syrup cannot depend on crystal structure, because the stuff is a perfectly uniform liquid, completely invariant under rotations in three-dimensional space. It can have no special axes, or any such thing. Optical activity must work very differently from birefringence.
You can find a clue to the nature of optical activity by considering what it looks like if you look at it in a mirror. If you reflect the system illustrated in Figure 12.7 in the x-z plane, by changing the sign of all the y coordinates, the angle θ changes to −θ. Thus the corn syrup that you see in a mirror must be fundamentally different from the corn syrup in your kitchen. This is not so strange. After all, your right hand looks like a left hand when you look at it in a mirror. The corn syrup must have the same property and have a definite “handedness.” In fact, because of the tetrahedral bonding of the carbon atoms of which they are built, the sugar molecules in the corn syrup can and do have such a handedness.
Because of the handedness of the sugar molecules, the index of refraction of the corn syrup actually depends on the handedness of the light. It is slightly different for left- and right-circularly polarized light. This happens because the →E field of a circularly polarized beam twists slightly as it traverses each sugar molecule and sees a slightly different electronic structure depending on the direction of the twist. Then, because the indices of refraction are slightly different, the left- and right-circularly polarized components of the light get different phase factors (kℓ) in passing through a thickness, ℓ, of the syrup.
We can now use our matrix language to see how this leads to optical activity. Up to an irrelevant overall phase, we can choose the phase produced on the left-circularly polarized light to be −θ and that on the right-circularly polarized light to be θ. Then we can represent the action of the syrup on an arbitrary wave by the matrix e−iθP++eiθP−,
where P± are matrices that pick out the left- and right-circularly polarized components, respectively. They satisfy P±(1±i)=(1±i),P±(1∓i)=0.
You can check that the matrices are P±=12(1∓i±i1).
Then (12.52) becomes e−iθ12(1−ii1)+eiθ12(1i−i1)=(cosθ−sinθsinθcosθ).
This is just the rotation matrix Rθ, of (12.34)! Rθ rotates both components of any light by an angle θ.
One might wonder about the reason for the handedness of the sugar molecules. In fact, there are physical processes, the weak interactions that give rise to β-radioactivity, that look different when reflected in a mirror3 and thus in principle could distinguish between left-handed and right-handed molecules. However, these interactions are most likely irrelevant to the handedness of corn syrup. Probably, the reason is biology rather than physics. Long ago, when the beginnings of life emerged from the primordial soup, purely by accident, the right-handed sugars were used. From then on, the handedness was maintained by the processes of reproduction.
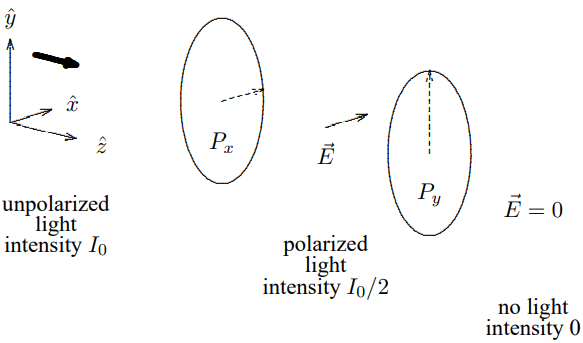
Figure 12.8: Initially unpolarized light passing through a pair of crossed polarizers.
Crossed Polarizers and Quantum Mechanics
Polarization offers many opportunities to get confused when you think of the light wave in terms of photons. Let us imagine turning down the intensity of the light to the point where one photon at a time is going through the polarizers and consider first the deceptively simple situation of light moving in the z direction through crossed polarizers in the x-y plane. Suppose that the first polarizer transmits light polarized in the x direction, and the second transmits light polarized in the y direction. This is deceptively simple because it seems that we can interpret what is going on simply in terms of photons. The situation is depicted in Figure 12.8. This seems simple enough to interpret in terms of photons. The unpolarized light in region I is composed equally of photons polarized in the x direction and in the y direction (goes the wrong “classical” argument). Those polarized in the x direction get through the first polarizer, so half the photons are still around in region II, where the intensity is reduced by half. Then none of these get through the second polarizer, so that the intensity in region III is zero.
But compare this with the apparently similar situation in which the second polarizer transmits light polarized at 45∘ in the x-y plane, as shown in Figure 12.9. Now the wave description tells us that the intensity in region III is reduced by another factor of 2 from that in region II. This is impossible to interpret in terms of classical particles. To see this, it is only necessary to turn down the intensity so that only one photon comes through at a time. Then the first polarizer is OK. As before, if the photon is polarized in the x direction, it get through. But now what happens at the second polarizer. The photon cannot split up. Either it gets through or it doesn’t. To be consistent with the wave description, in which the intensity is reduced by another factor of two, the transmission at the second polarizer must be a probabilistic event. Half the time the photon gets through. Half the time it is absorbed. There is no way for the
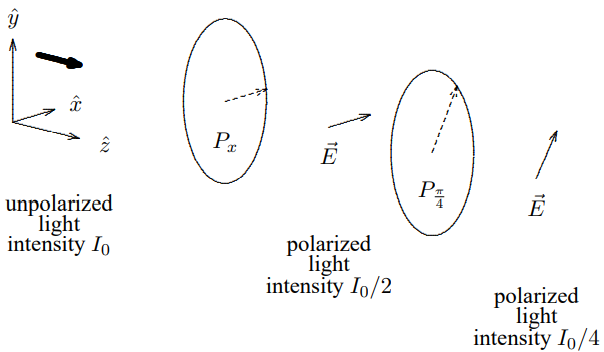
Figure 12.9: Initially unpolarized light passing through a pair of polarizers at with axes at 45∘.
photon in region II to tell whether it is going to make it! It is random. God plays dice.
__________________________
2 See Sears, Zemansky and Young, page 813.
3 They violate what is called “parity” symmetry.


