13.7: X-ray Diffraction

A beautiful three-dimensional example of diffraction from a periodic function is x-ray diffraction from crystals. A crystal is a regular array of atoms whose positions can be described by a periodic function \[f(\vec{r})=f(\vec{r}+\vec{a})\]

where \(\vec{a}\) is any vector from one point on the lattice to another. Mathematically, we can define the lattice as the set of all such vectors. Note that the lattice always includes the zero vector, the point at the origin. The three-dimensional Fourier transform of \(f(\vec{r})\) is nonzero only for wave number vectors of the form \[2 \pi \sum_{j=1}^{3} n_{j} \vec{\ell}_{j}\]

where \(\vec{\ell}_{j}\) are the basis vectors for the “dual” or “reciprocal” lattice that satisfies \[\vec{a} \cdot \vec{\ell}_{j}=\text { integer, for all } \vec{a}\]

The idea here is the same as the one-dimensional discussion of the diffraction grating, that \(k_{x}=2 \pi n / a\), (13.90). The derivation of (13.107) is precisely analogous to that of (13.90).

We can visualize the relation between the lattice and the dual lattice more easily for two-dimensional “crystals.” For example, consider a lattice of the form \[\vec{a}=n_{x} a_{x} \hat{x}+n_{y} a_{y} \hat{y}\]

shown in Figure \( 13.26\) (for \(a_{x}=2 a_{y}\)).

Figure \( 13.26\): A crystal lattice.

It is clear that vectors of the form \[\vec{\ell}_{1}=\frac{1}{a_{x}} \hat{x}, \quad \ell_{2}=\frac{1}{a_{y}} \hat{y},\]

satisfy (13.108). Furthermore, a little thought will convince you that these are the shortest pair of linearly independent vectors with this property. Thus we can take (13.110) to be the basis vectors for the dual lattice, so that the dual lattice looks like

\[\vec{d}_{m}=\left(\frac{m_{x}}{a_{x}} \hat{x}+\frac{m_{y}}{a_{y}} \hat{y}\right)\]

as shown in Figure \( 13.27\).Note that the long and short axes are interchanged, as usual in a diffraction process.

Figure \( 13.27\): The dual lattice.

Now suppose that there is a plane wave passing through the infinite lattice, \[e^{i \vec{k} \cdot \vec{r}-i \omega t} .\]

The wave that results from the interaction of the plane wave with the lattice then has the form \[e^{i \vec{k} \cdot \vec{r}-i \omega t} g(\vec{r}),\]

where \(g(\vec{r})\) is a periodic function, like \(f(\vec{r})\) in (13.106). To find the possible refracted waves, we must write this in the form: \[e^{i \vec{k} \cdot \vec{r}-i \omega t} g(\vec{r})=\sum_{\begin{array}{c}
\text { diffracted } \atop \text { waves }, \alpha
\end{array}} C_{\alpha} e^{i \vec{k}_{\alpha} \cdot \vec{r}-i \omega t} .\]

But we also know from the discussion above that the Fourier transform of \(g\) is nonzero only for values of \(\vec{k}\) of the form (13.107). Thus (13.114) takes the form \[e^{i \vec{k} \cdot \vec{r}-i \omega t} \int d^{3} k^{\prime} e^{i \vec{k}^{\prime} \cdot \vec{r}} C_{g}\left(\vec{k}^{\prime}\right)=e^{i \vec{k} \cdot \vec{r}-i \omega t} \sum_{n_{j}} C_{n_{j}} e^{2 \pi i \sum_{j} n_{j} \vec{\ell}_{j} \cdot \vec{r}}\]

Therefore, the \(\vec{k}_{\alpha}\) in (13.114) must have the form \[\vec{k}_{\alpha}=\vec{k} \mid 2 \pi \sum_{j} n_{j} \vec{\ell}_{j}\]

But this is only possible if \(\vec{k}_{\alpha}\) satisfies the dispersion relation in the material, which means, if the material is rotation invariant so that \(\omega^{2}\) depends only on \(|\vec{k}|^{2}\), that \[\left|\vec{k}_{\alpha}\right|^{2}=|\vec{k}|^{2}.\]

Thus we get a diffracted wave only for \(n_{j}\) such that (13.117) is satisfied. X-ray diffraction from a crystal, therefore, can provide direct information about the dual lattice and thus about the crystal lattice itself.

There is a more physical way of thinking about the dual lattice. Consider any vector in the dual lattice that is not a multiple of another, \[\vec{d} \equiv \sum_{j} n_{j} \vec{\ell}_{j}.\]

Now look at the subset of vectors on the lattice that satisfy \[\vec{d} \cdot \vec{a}=0.\]

This subset is the set of lattice points that lie in the plane, \(\vec{d} \cdot \vec{r}=0\), that is the plane perpendicular to \(\vec{d}\) passing through the origin. Now consider the subset \[\vec{d} \cdot \vec{a}=1.\]

This subset is the set of lattice points that lie in the plane, \(\vec{d} \cdot \vec{r}=1\), that is parallel to the plane \(\vec{d} \cdot \vec{r}=0\), in the lattice. This plane is also perpendicular to \(\vec{d}\) and passes through the point (which may not be a lattice point) \[r_{1}=\frac{\vec{d}}{|\vec{d}|^{2}}.\]

Therefore, the perpendicular distance (that is in the \(\vec{d}\) direction) between the two planes is \[\hat{d} \cdot \vec{r}_{1}=\frac{1}{|\vec{d}|}.\]

We can continue this discussion to conclude that the subset of lattice points satisfying \[\vec{d} \cdot \vec{a}=m \text { for integer } m=-\infty \text { to } \infty\]

is the set of lattice points lying on parallel planes perpendicular to \(\vec{d}\), with adjacent planes separated by \(1 /|\vec{d}|\). But this set must be all the lattice points! This is true because \(\vec{d} \cdot \vec{a}\) is an integer for all lattice points by the definition of the dual lattice. Thus all lattice points lie in one of the planes in (13.123).

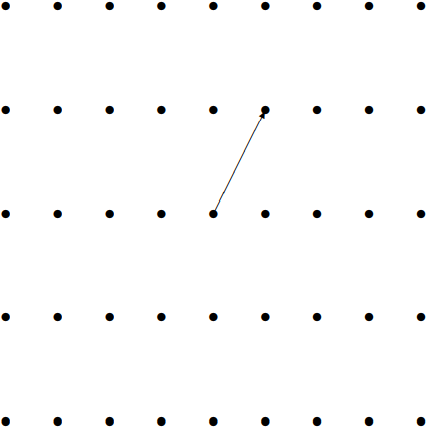
Figure \( 13.28\): A vector in the dual lattice.

These considerations are illustrated in the two-dimensional crystal in the pictures below. If the vector \(\vec{d}\) in the dual lattice is as shown in Figure \( 13.28\), then the perpendicular planes in the lattice are shown in Figure \( 13.29\).

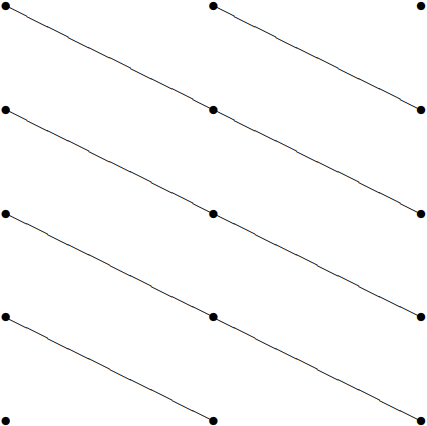
Figure \( 13.29\): The corresponding planes in the lattice.

Now suppose that \(\vec{d}\) is one of the special points in the dual lattice that gives rise to a refracted wave, so that \[|\vec{k}+2 \pi \vec{d}|^{2}=|\vec{k}|^{2} \Rightarrow \vec{d} \cdot(\vec{k}+\pi \vec{d})=0.\]

This relation is shown in Figure \( 13.30\). This shows that the \(k\) vector of the refracted wave, \(\vec{k}+2 \pi \vec{d}\), is just \(\vec{k}\) reflected in a plane perpendicular to \(\vec{d}\). We have seen that there are an

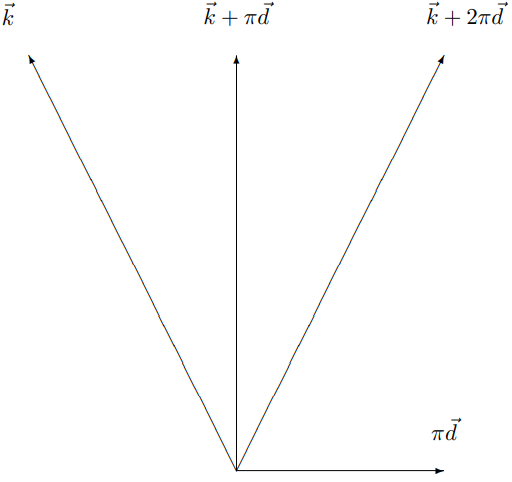
Figure \( 13.30\): The Bragg scattering condition.

infinite number of such planes in the lattice, separated by \(1 /|\vec{d}|\). The contribution to the scattered wave from each of these planes adds constructively to the refracted wave. To see this, consider the phase difference between the incoming wave, \(e^{i \vec{k} \cdot \vec{r}-i \omega t}\) and the diffracted wave \(e^{i \vec{k}_{\alpha} \cdot \vec{r}-i \omega t}\) for \(\vec{k}_{\alpha}=\vec{k}+2 \pi \vec{d}\). Evidently, the phase difference at any point \(\vec{r}\) is \[2 \pi \vec{d} \cdot \vec{r}.\]

This phase difference is an integral multiple of \(2\pi\) on all the planes \[\vec{d} \cdot \vec{r}=m \text { for integer } m=-\infty \text { to } \infty.\]

Thus the contribution to scattering from all of the planes of lattice points adds constructively, because the phase relation between the incoming and diffracted wave is the same on all of them. Conversely, if \(\vec{k}_{\alpha} \neq \vec{k}+2 \pi \vec{d}\), then the contribution from different planes will interfere destructively, and no diffracted wave will result.

This physical interpretation goes with the name “Bragg scattering.” The planes, (13.123) (or (13.126)) are the Bragg planes of the crystal. Note that as the vector \(\vec{d}\) in the dual lattice gets longer, the corresponding Bragg planes get closer together, but they are also less dense, containing fewer scattering centers per unit area. Generally the scattering is weaker for large \(|\vec{d}|\).