13.8: Chapter Checklist

You should now be able to:

1. i. Be able to set up a diffraction problem as a forced oscillation problem and write the diffracted wave as a Fourier integral;
2. Interpret the Fourier integral in the far-field region and find the diffraction pattern;
3. Analyze the diffraction patterns in beams made with one or more slits and rectangles;
4. Use the convolution theorem to simplify the calculation of Fourier transforms;
5. Analyze the scattering from a diffraction grating and x-ray diffraction from crystals;
6. Interpret a hologram as a diffraction pattern;
7. Understand how a zone plate can focus a plane wave.

Problems

13.1. Consider the transverse oscillations of a semi-infinite, flexible membrane with surface tension \(T_{S}\) and surface mass density \(\rho_{S}\). The membrane is stretched in the \(z\) = 0 plane from \(y = −\infty\) to \(\infty\) and from \(x = 0\) to \(\infty\). The membrane is held fixed along the half lines, \(x=z=0\), \(a \leq y \leq \infty\) and \(x = z = 0\), \(-\infty \leq y \leq-a\). For \(y\) between \(a\) and \(-a\), the membrane is driven with frequency \(\omega\) so that the end at \(x = 0\) moves with transverse displacement \[\psi(0, y, t)=f(y) e^{-i \omega t}\]

where \[f(y)=\left\{\begin{array}{cl}
b\left(1-\frac{y}{a}\right) & \text { for } 0 \leq y \leq a \\
b\left(1+\frac{y}{a}\right) & \text { for }-a \leq y \leq 0 \\
0 \quad & \text { for }|y| \geq a.
\end{array}\right.\]

The transverse displacement is given by \[\psi(x, y, t)=\int_{-\infty}^{\infty} d k_{y} C\left(k_{y}\right) e^{i\left(y k_{y}+x k\left(k_{y}\right)-\omega t\right)}\]

where \(k(k_{y})\) is some function of \(k_{y}\) and \[C\left(k_{y}\right)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} d y f(y) e^{-i k_{y} y}=\frac{b}{\pi k_{y}^{2} a}\left(1-\cos k_{y} a\right).\]

Find the function \(k(k_{y})\).

If the intensity of the wave at \(x = L\), \(y = 0\) for large \(L\) is \(I_{0}\), find the intensity for \(x = L\) and any value of \(y\). Hint: Assume that you are in the far field region, and account for all the relevant factors contributing to the ratio of the intensity to \(I_{0}\).

13.2. Consider an opaque barrier in the \(x\)-\(y\) plane at \(z = 0\), with a single slit along the \(x\) axis of width \(2a\), but with regions on either side of the slit each with width \(2a\) which are partially transparent, designed to reduce the intensity by a factor of 2. When this barrier is illuminated by a plane wave in the \(z\) direction, the amplitude of the oscillating field at \(z = 0\) is \[f(x, y) e^{-i \omega t}\]

for \[f(x, y)=\left\{\begin{array}{ccc}
1 & \text { for } & |y|<a \\
1 / \sqrt{2} & \text { for } & a<|y|<3 a \\
0 & \text { for } & 3 a<|y|.
\end{array}\right.\]

Near the slit, this just produces a beam which is less intense by a factor of two on the edges. Far away, however, the diffraction pattern is quite different from that of the single slit. At a fixed large distance \(R=\sqrt{y^{2}+z^{2}}\) away from the slit, the intensity as a function of \[\xi=k_{y} a=\frac{\omega y a}{c R}\]

is shown in the graph in Figure \( 13.38\) for positive \(\xi\). The value of the peak at \(\xi = 0\) is normalized to 1, but has been suppressed in the graph to show the details of the secondary maxima.

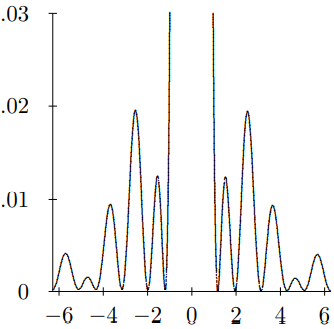
Figure \( 13.38\): Problem 13.2.

Find the smallest positive value of \(\xi\) for which the intensity vanishes.

Find the ratio of the intensity at \(\xi=\pi / 2\) to that at \(\xi = 0\).

So far we have not mentioned the polarization of the light, assuming that it is irrelevant. In fact, we get the pattern shown above for any polarization, so long as the shading doesn’t effect the polarization (and \(\xi\) is small). However, if the light is initially polarized in the direction \(45^{\circ}\) from the \(x\) axis, we could reduce the intensity by two by passing it through a perfect polarizer aligned with the \(y\) axis. Suppose that our slit between \(-a\) and \(a\) is completely empty, but between \(-3a\) and \(-a\) and between \(a\) and \(3a\), we put such a polarizer. Now, as before, the beam close to the slit just has the intensity on the edges reduced by a factor of 2. Now, however, the diffraction pattern is quite different. As a function of \(\xi\), the intensity at large fixed \(R\) is \[\propto \frac{1}{10}\left[\left(\frac{\sin 3 \xi}{\xi}\right)^{2}+\left(\frac{\sin \xi}{\xi}\right)^{2}\right]\]

which looks nothing like the pattern above. Explain the difference.

13.3. Consider an opaque barrier in the \(x\)-\(y\) plane at \(z = 0\), with identical holes centered at \((x, y)=\left(n_{x} a, n_{y} a\right)\) for all integers \(n_{x}\) and \(n_{y}\). Suppose that the barrier is illuminated from \(z<0\) by a plane wave traveling in the z direction with wavelength \(\lambda=a \sqrt{3} / 2 \text { . }\).

For \(z > 0\), the wave has the form \[\sum_{m_{x}, m_{y}} C_{m_{x}, m_{y}} e^{i\left(m_{x} \rho x+m_{y} \rho y+k_{z}\left(m_{x}, m_{y}\right) z-\omega t\right)}\]

where \(m_{x}\) and \(m_{y}\) run over all integers.

Find \(\rho\).

For large \(z\), only a finite number of terms in the sum are important. How many and how do you know?

Now suppose that instead of coming in the \(z\) direction, a plane wave with the same wavelength is moving for \(z < 0\) at \(45^{\circ}\) to the \(z\) axis both in the \(x\)-\(z\) plane, and in the \(y\)-\(z\) plane. That is \[\frac{k_{x}}{k_{z}}=\frac{k_{y}}{k_{z}}=\operatorname{lan} 45^{\circ}=1 .\]

Now for \(z > 0\), the wave has the form \[\sum_{m_{x}, m_{y}} C_{m_{x}, m_{y}} e^{i\left[\left(m_{x} \rho+\xi_{x}\right) x+\left(m_{y} \rho+\xi_{y}\right) y+k_{z}\left(m_{x}, m_{y}\right) z-\omega t\right]}\]

where \(m_{x}\) and \(m_{y}\) run over all integers.

Find \(\xi_{x}\) and \(\xi_{y}\).

Again for large \(z\), only a finite number of terms in the sum are important. Which ones — that is, what values of \(m_{x}\) and \(m_{y}\)?

13.4. Describe the diffraction pattern that results when a transmission diffraction grating with line separation distance \(S\) is illuminated by a plane wave of monochromatic light with wavelength \(L\) that is traveling in a direction perpendicular to the grating lines and at an angle \(\theta\) to the perpendicular from the surface of the grating.

13.5. An opaque screen with four narrow slits at \(x=\pm 0.6 \mathrm{~mm}\) and \(x=\pm 0.4 \mathrm{~mm}\) is blocking a beam of coherent light with wavelength \(4 \times 10^{-5} \mathrm{~cm}\). Describe the diffraction pattern that appears on a screen 5 meters away.

13.6. A semi-infinite flexible membrane is stretched in the \(z = 0\) plane for \(x \geq 0\) with surface tension \(T_{s}\) and surface mass density \(\rho_{s}\). The membrane is clamped down at \(z = 0\) along the two semi-infinite lines, \(z = 0\), \(x = 0\), \(y \geq a\) and \(z = 0\), \(x = 0\), \(y \leq-a\). For \(-a \leq y \leq a\) and \(x = 0\), the membrane is forced to oscillate with an amplitude of the form \[z=B e^{i \omega t} \cos \frac{\pi y}{2 a}.\]

Draw a diagram of the \(z = 0\) half plane for \(x \geq 0\) and indicate where the average of the absolute value square of the transverse displacement of the membrane is large (i.e. not much smaller than \(B^{2} a / r\), where \(r\) is the distance from the origin). For your diagram, assume that the distance \(a\) is about 5 times the wavelength of the waves.

Find the intensity of the disturbance on the membrane produced by this forced oscillation as a function of \(\theta=\tan ^{-1}(y / x)\) on a large semicircle, \(x^{2}+y^{2}=R^{2}\), for \(R^{2}>>a^{4} \omega^{2} \rho_{s} / T_{s}\).

Hint: This is similar to a single slit diffraction problem. Note that even though the disturbance is a cosine, you will have to do a Fourier integral (although not a difficult one) to do part b, because the disturbance is confined to \(-a \leq y \leq a\) at \(x = 0\).

13.7. Suppose that a diffraction grating with line separation \(d\) is etched onto the top of a thick piece of glass with index of refraction \(n\). If light of frequency \(\omega\) is incident on the top, coming in at an angle \(\theta\) from the perpendicular to the face and perpendicular to the grating lines, find the angles of the components of the wave in the glass.

13.8. Shown in Figure \( 13.39\) are 4 diffraction patterns such as might be produced by shining laser light (nearly a plane wave) through a slit or slits, and projecting the pattern onto a photographic plate far away. The patterns are each produced by about 500 individual photons striking the plate with a probability density proportional to the intensity of the diffracted wave.

Figure \( 13.39\): Four diffraction patterns.

The four objects that produced these patterns were, in a random order,

1. A single slit, 1 mm wide;
2. A single slit, 0.6 mm wide;
3. Two slits, each 0.6 mm wide, with centers 1.5 mm apart;
4. Six slits, each 0.6 mm wide, with adjacent centers 1.5 mm apart.

1. Which is which?
2. How do you know?