3.4: Coulomb's Law

Learning Objectives

By the end of this section, you will be able to:

• State Coulomb’s law in terms of how the electrostatic force changes with the distance between two objects.
• Calculate the electrostatic force between two charged point forces, such as electrons or protons.
• Compare the electrostatic force to the gravitational attraction for a proton and an electron; for a human and the Earth.

Through the work of scientists in the late 18th century, the main features of the electrostatic force—the existence of two types of charge, the observation that like charges repel, unlike charges attract, and the decrease of force with distance—were eventually refined, and expressed as a mathematical formula. The mathematical formula for the electrostatic force is called Coulomb’s law after the French physicist Charles Coulomb (1736–1806), who performed experiments and first proposed a formula to calculate it.

Figure $\PageIndex{1}$: This NASA image of Arp 87 shows the result of a strong gravitational attraction between two galaxies. In contrast, at the subatomic level, the electrostatic attraction between two objects, such as an electron and a proton, is far greater than their mutual attraction due to gravity. (credit: NASA/HST)

Definition: Coulomb’s Law

Coulomb’s law calculates the magnitude of the force $F$ between two point charges, $q_1$ and $q_2$, separated by a distance $r$.

$$F=k\dfrac{|q_{1}q_{2}|}{r^{2}}.$$

In SI units, the constant$k$ is equal to

$$k=8.988\times 10^{9}\dfrac{N\cdot m^{2}}{C^{2}}\approx 8.99\times 10^{9}\dfrac{N\cdot m^{2}}{C^{2}}.$$

The electrostatic force is a vector quantity and is expressed in units of newtons. The force is understood to be along the line joining the two charges. (Figure $\PageIndex{2}$)

Although the formula for Coulomb’s law is simple, it was no mean task to prove it. The experiments Coulomb did, with the primitive equipment then available, were difficult. Modern experiments have verified Coulomb’s law to great precision. For example, it has been shown that the force is inversely proportional to distance between two objects squared $(F\propto 1/r^{2})$ to an accuracy of 1 part in $10^{16}$. No exceptions have ever been found, even at the small distances within the atom.

Figure $\PageIndex{2}$: The magnitude of the electrostatic force$F$ between point charges $q_{1}$ and $q_{2}$ separated by a distance $r$ is given by Coulomb’s law. Note that Newton’s third law (every force exerted creates an equal and opposite force) applies as usual—the force on $q_{1}$ is equal in magnitude and opposite in direction to the force it exerts on $q_{2}$. (a) Like charges. (b) Unlike charges.

Example$\PageIndex{1}$: How Strong is the Coulomb Force Relative to the Gravitational Force?

Compare the electrostatic force between an electron and proton separated by $0.530\times 10^{-10}m$ with the gravitational force between them. This distance is their average separation in a hydrogen atom.

Strategy

To compare the two forces, we first compute the electrostatic force using Coulomb’s law, $F=k\dfrac {|q_{1}q_{2}}{r^{2}}$. We then calculate the gravitational force using Newton’s universal law of gravitation. Finally, we take a ratio to see how the forces compare in magnitude.

Solution

Entering the given and known information about the charges and separation of the electron and proton into the expression of Coulomb’s law yields

$$\begin{align*} F &=k\dfrac{|q_{1}q_{2}|}{r^2} \\[5pt] &=(8.99\times 10^{9} N\cdot m^{2}/C^{2})\times \dfrac{(1.60\times 10^{-19}C)(1.60\times 10^{-19}C)}{(0.530\times 10^{-10}m)^{2}} \end{align*}$$

Thus the Coulomb force is

$$F=8.19\times 10^{-8}N. \nonumber$$

The charges are opposite in sign, so this is an attractive force. This is a very large force for an electron—it would cause an acceleration of $8.99\times 10^{22} m/s^{2}$(verification is left as an end-of-section problem).The gravitational force is given by Newton’s law of gravitation as:

$$F_{G}=G\dfrac{mM}{r^2},\nonumber$$

where $G=6.67\times 10^{-11} N\cdot m^{2}/kg^{2}$. Here $m$ and $M$ represent the electron and proton masses, which can be found in the appendices. Entering values for the knowns yields

$$F_{G}=(6.67\times 10^{-11} N\cdot m^{2}/kg^{2})\times \dfrac{(9.11\times 10^{-31}kg)(1.67\times 10^{-27}kg)}{(0.530\times 10^{-10}m)^{2}}=3.61\times 10^{-47}N \nonumber$$

This is also an attractive force, although it is traditionally shown as positive since gravitational force is always attractive. The ratio of the magnitude of the electrostatic force to gravitational force in this case is, thus,

$$\dfrac{F}{F_{G}}=2.27\times 10^{39}. \nonumber$$

 

Discussion

This is a remarkably large ratio! Note that this will be the ratio of electrostatic force to gravitational force for an electron and a proton at any distance (taking the ratio before entering numerical values shows that the distance cancels). This ratio gives some indication of just how much larger the Coulomb force is than the gravitational force between two of the most common particles in nature.

As the example implies, gravitational force is completely negligible on a small scale, where the interactions of individual charged particles are important. On a large scale, such as between the Earth and a person, the reverse is true. Most objects are nearly electrically neutral, and so attractive and repulsive Coulomb forces nearly cancel. Gravitational force on a large scale dominates interactions between large objects because it is always attractive, while Coulomb forces tend to cancel.

Example $\PageIndex{2}$: The Force on the Electron in Hydrogen

A hydrogen atom consists of a single proton and a single electron. The proton has a charge of $+e$ and the electron has $-e$. In the “ground state” of the atom, the electron orbits the proton at most probable distance of $5.29 \times 10^{-11} m$ (Figure $\PageIndex{2}$). Calculate the electric force on the electron due to the proton.

Figure $\PageIndex{3}$: A schematic depiction of a hydrogen atom, showing the force on the electron. This depiction is only to enable us to calculate the force; the hydrogen atom does not really look like this.

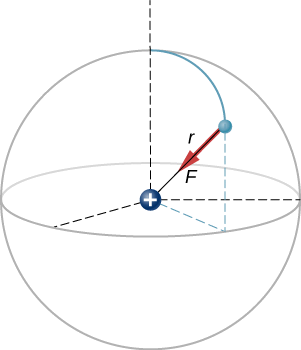
Strategy

For the purposes of this example, we are treating the electron and proton as two point particles, each with an electric charge, and we are told the distance between them; we are asked to calculate the force on the electron. We thus use Coulomb’s law (Equation $\ref{Coulomb}$).

Answer

Our two charges are,

$$\begin{align*} q_1 &= +e \\[4pt] &= +1.602 \times 10^{-19} C \\[4pt] q_2 &= -e \\[4pt] &= -1.602 \times 10^{-19} C \end{align*}$$

and the distance between them

$$r = 5.29 \times 10^{-11} m. \nonumber$$

The magnitude of the force on the electron (Equation $\ref{Coulomb}$) is

$$\begin{align*} F &= \dfrac{1}{4\pi \epsilon_0}\dfrac{|q_1q_2|}{r_{12}^2} \\[4pt] &= \dfrac{1}{4\pi \left(8.85 \times 10^{-12} \frac{C^2}{N \cdot m^2} \right)} \dfrac{(1.602 \times 10^{-19} C)^2}{(5.29 \times 10^{-11} m)^2} \\[4pt] &= 8.25 \times 10^{-8} \end{align*}$$

As for the direction, since the charges on the two particles are opposite, the force is attractive; the force on the electron points radially directly toward the proton, everywhere in the electron’s orbit. The force is thus expressed as

$$\vec{F} = (8.25 \times 10^{-8} N) \hat{r}. \nonumber$$

Multiple Source Charges

The analysis that we have done for two particles can be extended to an arbitrary number of particles; we simply repeat the analysis, two charges at a time. Specifically, we ask the question: Given N charges (which we refer to as source charge), what is the net electric force that they exert on some other point charge (which we call the test charge)?

Like all forces that we have seen up to now, the net electric force on our test charge is simply the vector sum of each individual electric force exerted on it by each of the individual test charges. Thus, we can calculate the net force on the test charge Q by calculating the force on it from each source charge, taken one at a time, and then adding all those forces together (as vectors). This ability to simply add up individual forces in this way is referred to as the principle of superposition, and is one of the more important features of the electric force. In mathematical form, this becomes

$$\vec{F}(r) = \dfrac{1}{4\pi \epsilon_0} Q \sum_{i=1}^N \dfrac{q_i}{r_i^2}\hat{r}_i. \label{sup}$$

In this expression, Q represents the charge of the particle that is experiencing the electric force $\vec{F}$, and is located at $\vec{r}$ from the origin; the $q_i's$ are the N source charges, and the vectors $\vec{r}_i$ are the displacements from the position of the ith charge to the position of $Q$. In the notation used for vector $\vec{r}_i$, $r_i$ refers to the magnitude of the vector, and unit vector $\hat{r}_i$ refers to its direction. Each of the N unit vectors points directly from its associated source charge toward the test charge. All of this is depicted in Figure $\PageIndex{2}$. Please note that there is no physical difference between Q and $q_i$; the difference in labels is merely to allow clear discussion, with Q being the charge we are determining the force on.

Figure $\PageIndex{4}$: The eight source charges each apply a force on the single test charge Q. Each force can be calculated independently of the other seven forces. This is the essence of the superposition principle.

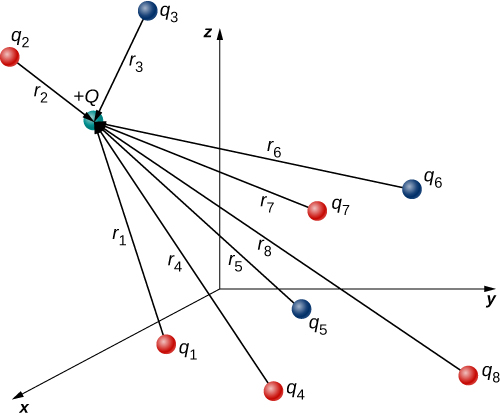
(Note that the force vector $\vec{F}_i$ does not necessarily point in the same direction as the unit vector $\hat{r}_i$; it may point in the opposite direction, $-\hat{r}_i$. The signs of the source charge and test charge determine the direction of the force on the test charge.)

Example $\PageIndex{3}$: The Net Force from Two Source Charges

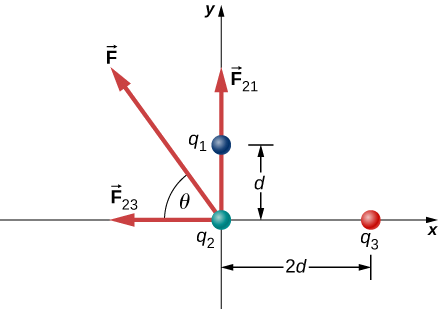
Three different, small charged objects are placed as shown in Figure $\PageIndex{5}$. The charges $q_1$ and $q_3$ are fixed in place; $q_2$ is free to move. Given $q_1 = 2e, \, q_2 = -3e$, and $q_3 = -5e$, and that $d = 2.0 \times 10^{-7} m$, what is the net force on the middle charge $q_2$?

Figure $\PageIndex{5}$: Source charges $q_1$ and $q_3$ each apply a force on $q_2$.

Strategy

We use Coulomb’s law. The principle of superposition says that the force on $q_2$ from each of the other charges is unaffected by the presence of the other charge. Therefore, we write down the force on $q_2$ from each and add them together as vectors.

Solution

We have two source charges $q_1$ and $q_3$ a test charge $q_2$, distances $r_{21}$ and $r_{23}$ and we are asked to find a force. This calls for Coulomb’s law and superposition of forces. There are two forces:

$$\begin{align*} \vec{F} &= \vec{F}_{21} + \vec{F}_{23}. \end{align*}$$

	x-component	y-component
$\vec{F}_{21}$	$F_{21_{x}}=0$	$F_{21_{y}}=\dfrac{1}{4\pi \epsilon_0}\left[\dfrac{q_2q_1}{r_{21}^2}\right]$
$\vec{F}_{23}$	$F_{23_{x}}=\dfrac{1}{4\pi \epsilon_0}\left[-\dfrac{q_2q_3}{r_{23}^2}\right]$	$F_{23_{y}}=0$
$\vec{F}=\vec{F}_{21}+\vec{F}_{23}$	$F_{x}=F_{21_{x}}+F_{23_{x}}=\dfrac{1}{4\pi \epsilon_0}\left[-\dfrac{q_2q_3}{r_{23}^2}\right]$	$F_{y}=F_{21_{y}}+F_{23_{y}}=\dfrac{1}{4\pi \epsilon_0}\left[\dfrac{q_2q_1}{r_{21}^2}\right]$

We cannot add these forces directly because they don’t point in the same direction: $\vec{F}_{12}$ points only in the −x-direction, while $\vec{F}_{13}$ points only in the +y-direction. The net force is obtained from applying the Pythagorean theorem to its x- and y-components:

$$F = \sqrt{F_x^2 + F_y^2} \nonumber$$

and

$$\begin{align*} F_x &= -F_{23} = -\dfrac{1}{4\pi \epsilon_0} \dfrac{q_2q_3}{r_{23}^2} \\[4pt] &= - \left(8.99 \times 10^9 \dfrac{N\cdot m^2}{C^2}\right) \dfrac{(4.806 \times 10^{-19} C)(8.01 \times 10^{-19}C)}{(4.00 \times 10^{-7}m)^2} \\[4pt] &= -2.16 \times 10^{-14} \, N\end{align*}$$

and

$$\begin{align*}F_y &= F_{21} = \dfrac{1}{4\pi \epsilon_0} \dfrac{q_2q_1}{r_{21}} \\[4pt] &= \left(9.99 \times 10^9 \dfrac{N \cdot m^2}{C^2}\right) \dfrac{(4.806 \times 10^{-19}C)(3.204 \times 10^{-19}C)}{(2.00 \times 10^{-7} m)^2} \\[4pt] &= 3.46 \times 10^{-14} \, N.\end{align*}$$

We find that

$$\begin{align*} F &= \sqrt{F_x^2 + F_y^2} \\[4pt] &= 4.08 \times 10^{-14} \, N \end{align*}$$

at an angle of

$$\begin{align*} \phi &= \tan^{-1} \left(\dfrac{F_y}{F_x}\right) \\[4pt] &= \tan^{-1} \left( \dfrac{3.46 \times 10^{-14} N}{-2.16 \times 10^{-14}N} \right) \\[4pt] &= -58^o, \end{align*}$$

that is, $58^o$ above the −x-axis, as shown in the diagram.

Significance

Notice that when we substituted the numerical values of the charges, we did not include the negative sign of either $q_1$ or $q_3$. Recall that negative signs on vector quantities indicate a reversal of direction of the vector in question. But for electric forces, the direction of the force is determined by the types (signs) of both interacting charges; we determine the force directions by considering whether the signs of the two charges are the same or are opposite. If you also include negative signs from negative charges when you substitute numbers, you run the risk of mathematically reversing the direction of the force you are calculating. Thus, the safest thing to do is to calculate just the magnitude of the force, using the absolute values of the charges, and determine the directions physically.

It’s also worth noting that the only new concept in this example is how to calculate the electric forces; everything else (getting the net force from its components, breaking the forces into their components, finding the direction of the net force) is the same as force problems you have done earlier.

Summary

• Frenchman Charles Coulomb was the first to publish the mathematical equation that describes the electrostatic force between two objects.
• Coulomb’s law gives the magnitude of the force between point charges. It is $F=k\dfrac{|q_{1}q_{2}|}{r^{2}},$ where $q_{1}$ and $q_{2}$ are two point charges separated by a distance $r$, and $k\approx 8.99\times 10^{9}N\cdot m^{2}/C^{2}$
• This Coulomb force is extremely basic, since most charges are due to point-like particles. It is responsible for all electrostatic effects and underlies most macroscopic forces.
• The Coulomb force is extraordinarily strong compared with the gravitational force, another basic force—but unlike gravitational force it can cancel, since it can be either attractive or repulsive.
• The electrostatic force between two subatomic particles is far greater than the gravitational force between the same two particles.

Glossary

Coulomb’s law

the mathematical equation calculating the electrostatic force vector between two charged particles

Coulomb force

another term for the electrostatic force

electrostatic force

the amount and direction of attraction or repulsion between two charged bodies