2.3: Triangles
( \newcommand{\kernel}{\mathrm{null}\,}\)
6.1.2: Triangles
- Identify equilateral, isosceles, scalene, acute, right, and obtuse triangles.
- Identify whether triangles are similar, congruent, or neither.
- Identify corresponding sides of congruent and similar triangles.
- Find the missing measurements in a pair of similar triangles.
- Solve application problems involving similar triangles
Introduction
Geometric shapes, also called figures, are an important part of the study of geometry. The triangle is one of the basic shapes in geometry. It is the simplest shape within a classification of shapes called polygons. All triangles have three sides and three angles, but they come in many different shapes and sizes. Within the group of all triangles, the characteristics of a triangle’s sides and angles are used to classify it even further. Triangles have some important characteristics, and understanding these characteristics allows you to apply the ideas in real-world problems.
Classifying and Naming Triangles
A polygon is a closed plane figure with three or more straight sides. Polygons each have a special name based on the number of sides they have. For example, the polygon with three sides is called a triangle because “tri” is a prefix that means “three.” Its name also indicates that this polygon has three angles. The prefix “poly” means many.
The table below shows and describes three classifications of triangles. Notice how the types of angles in the triangle are used to classify the triangle.
| Name of Triangle | Picture of Triangle | Description |
| Acute Triangle | 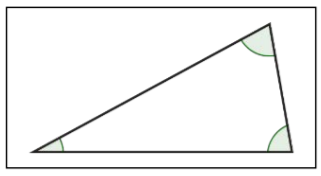 |
A triangle with 3 acute angles (3 angles measuring between 0° and 90°). |
| Obtuse Triangle | 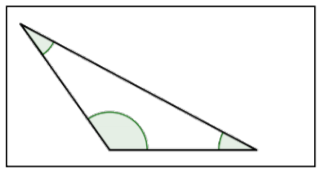 |
A triangle with 1 obtuse angle (1 angle measuring between 90° and 180°). |
| Right Triangle | 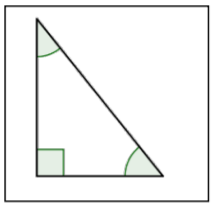 |
A triangle containing one right angle (1 angle that measures 90°). Note that the right angle is shown with a corner mark and does not need to be labeled 90°. |
The sum of the measures of the three interior angles of a triangle is always 180°. This fact can be applied to find the measure of the third angle of a triangle, if you are given the other two. Consider the examples below.
A triangle has two angles that measure 35° and 75°. Find the measure of the third angle.
Solution
The sum of the three interior angles of a triangle is 180°.
35° + 75° + x = 180°
Find the value of x.
110º + x = 180º
x = 180° ‒ 110º
x = 70°
Answer: The third angle of the triangle measures 70°.
One of the angles in a right triangle measures 57º. Find the measurement of the third angle.
Solution
The sum of the three angles of a triangle is 180°. One of the angles has a measure of 90° as it is a right triangle.
57° + 90° + x = 180°
Simplify.
147º + x = 180°
Find the value of x.
x = 180º - 147º
x = 33º
Answer: The third angle of the right triangle measures 33°.
There is an established convention for naming triangles. The labels of the vertices of the triangle, which are generally capital letters, are used to name a triangle.
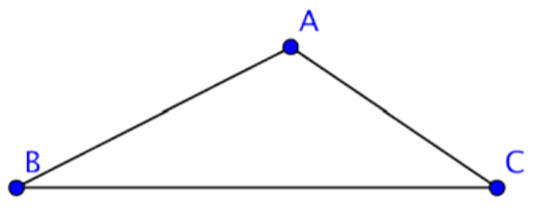
You can call this triangle ABC or ∆ABC since A, B, and C are vertices of the triangle. When naming the triangle, you can begin with any vertex. Then keep the letters in order as you go around the polygon. The triangle above could be named in a variety of ways: ∆ABC, or ∆CBA. The sides of the triangle are line segments AB, AC, and CB.
Just as triangles can be classified as acute, obtuse, or right based on their angles, they can also be classified by the length of their sides. Sides of equal length are called congruent sides. While we designate a segment joining points A and B by the notation ¯AB, we designate the length of a segment joining points A and B by the notation AB without a segment bar over it. The length AB is a number, and the segment ¯AB is the collection of points that make up the segment.
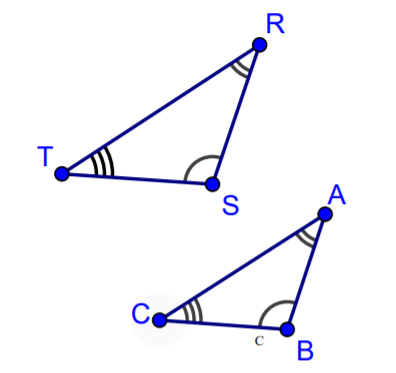
Mathematicians show congruency by putting a hash mark symbol through the middle of sides of equal length. If the hash mark is the same on one or more sides, then those sides are congruent. If the sides have different hash marks, they are not congruent. The table below shows the classification of triangles by their side lengths.
| Name of Triangle | Picture of Triangle | Description |
| Equilateral Triangle | 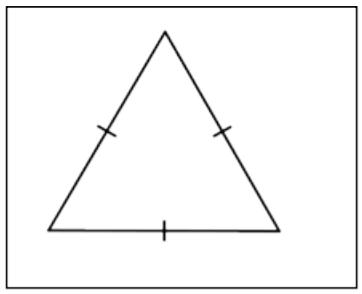 |
A triangle whose three sides have the same length. These sides of equal length are called congruent sides. |
| Isosceles Triangle | 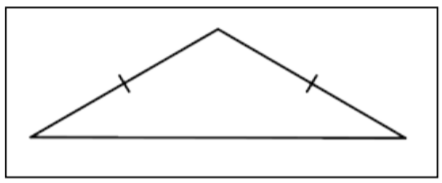 |
A triangle with exactly two congruent sides. |
| Scalene Triangle | 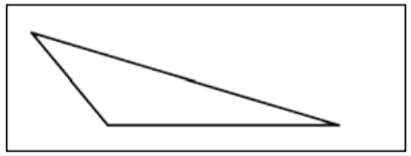 |
A triangle in which all three sides are a different length. |
To describe a triangle even more specifically, you can use information about both its sides and its angles. Consider this example.
Classify the triangle below.
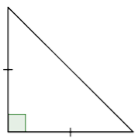
Solution
Notice what kind of angles the triangle has. Since one angle is a right angle, this is a right triangle.
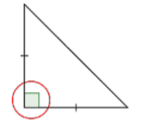
Notice the lengths of the sides. Are there congruence marks or other labels?
The congruence marks tell us there are two sides of equal length. So, this is an isosceles triangle.
Answer: This is an isosceles right triangle
Classify the given triangle.
Identifying Congruent and Similar Triangles
Two triangles are congruent if they are exactly the same size and shape. In congruent triangles, the measures of corresponding angles and the lengths of corresponding sides are equal. Consider the two triangles shown below:
Since both ∠B and ∠E are right angles, these triangles are right triangles. Let’s call these two triangles ∆ABC and ∆DEF. These triangles are congruent if every pair of corresponding sides has equal lengths and every pair of corresponding angles has the same measure.
The corresponding sides are opposite the corresponding angles.
↔ means “corresponds to”
∠B ↔ ∠E
∠A ↔ ∠D
∠C ↔ ∠F
¯AB ↔ ¯DE
¯AC ↔ ¯DF
¯BC ↔ ¯EF
∆ABC and ∆DEF are congruent triangles as the corresponding sides and corresponding angles are equal.
Let’s take a look at another pair of triangles. Below are the triangles ∆ABC and ∆RST.
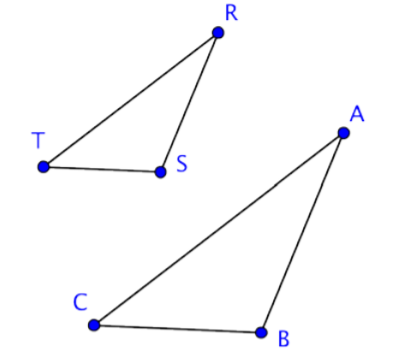
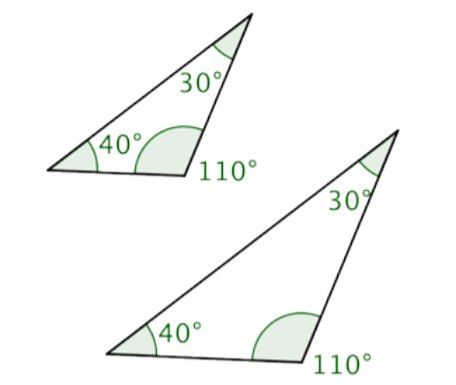
These two triangles are surely not congruent because ∆RST is clearly smaller in size than ∆ABC. But, even though they are not the same size, they do resemble one another. They are the same shape. The corresponding angles of these triangles look like they might have the same exact measurement, and if they did they would be congruent angles and we would call the triangles similar triangles.
Congruent angles are marked with hash marks, just as congruent sides are.
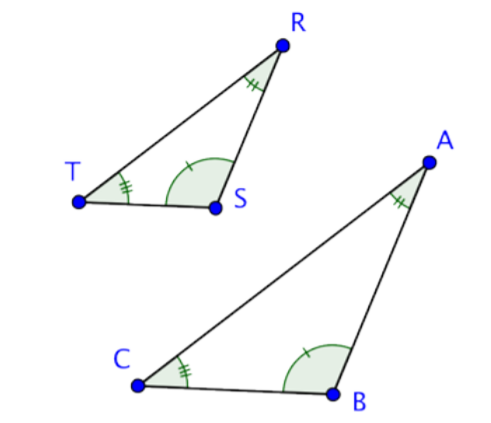
We can also show congruent angles by using multiple bands within the angle, rather than multiple hash marks on one band. Below is an image using multiple bands within the angle.
If the corresponding angles of two triangles have the same measurements they are called similar triangles. This name makes sense because they have the same shape, but not necessarily the same size. When a pair of triangles is similar, the corresponding sides are proportional to one another. That means that there is a consistent scale factor that can be used to compare the corresponding sides. In the previous example, the side lengths of the larger triangle are all 1.4 times the length of the smaller. So, similar triangles are proportional to one another.
Just because two triangles look similar does not mean they are similar triangles in the mathematical sense of the word. Checking that the corresponding angles have equal measure is one way of being sure the triangles are similar.
Corresponding Sides of Similar Triangles
There is another method for determining similarity of triangles that involves comparing the ratios of the lengths of the corresponding sides.
If the ratios of the pairs of corresponding sides are equal, the triangles are similar.
Consider the two triangles below.
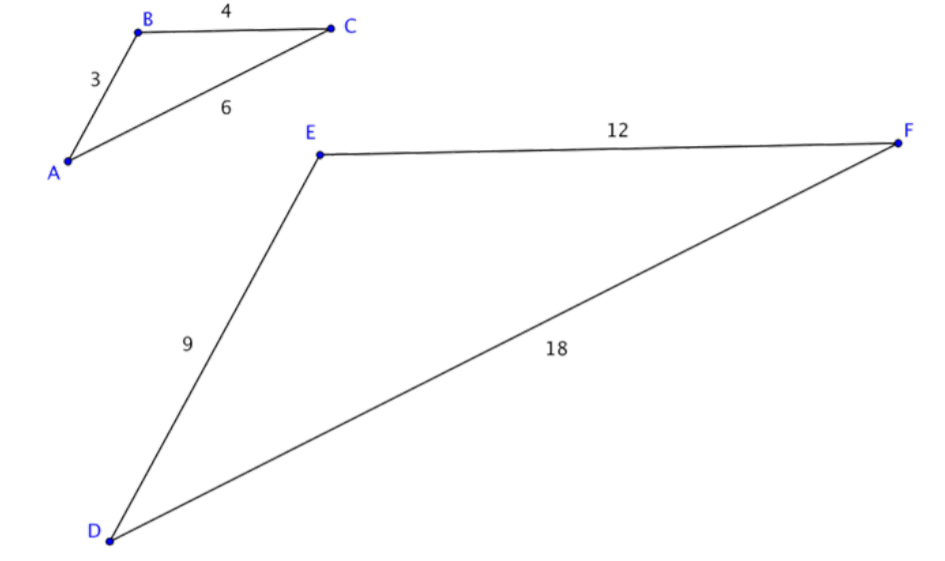
∆ABC is not congruent to ∆DEF because the side lengths of ∆DEF are longer than those of ∆ABC. So, are these triangles similar? If they are, the corresponding sides should be proportional.
Since these triangles are oriented in the same way, you can pair the left, right, and bottom sides: ¯AB and ¯DE, ¯BC and ¯EF, ¯AC and ¯DF. (You might call these the two shortest sides, the two longest sides, and the two leftover sides and arrive at the same ratios). Now we will look at the ratios of their lengths.
¯AB¯DE=¯BC¯EF=¯AC¯DF
Substituting the side length values into the proportion, you see that it is true:
39=412=618
If the corresponding sides are proportional, then the triangles are similar. Triangles ABC and DEF are similar, but not congruent.
Let’s use this idea of proportional corresponding sides to determine whether two more triangles are similar.
Determine if the triangles below are similar by seeing if their corresponding sides are proportional.
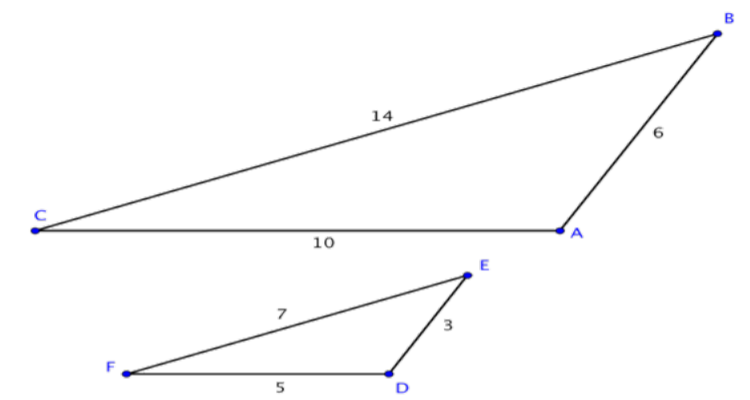
Solution
First determine the corresponding sides, which are opposite corresponding angles.
¯CA ↔ ¯FD
¯AB ↔ ¯DE
¯BC ↔ ¯EF
Write the corresponding side lengths as ratios.
¯CA¯FD=¯AB¯DE=¯BC¯EF
Substitute the side lengths into the ratios, and determine if the ratios of the corresponding sides are equivalent. They are, so the triangles are similar.
105=63=147
2=2=2
Answer: ∆ABC and ∆DEF are similar.
The mathematical symbol ~ means “is similar to”. So, you can write ∆ABC is similar to ∆DEF as ∆ABC ~ ∆DEF.
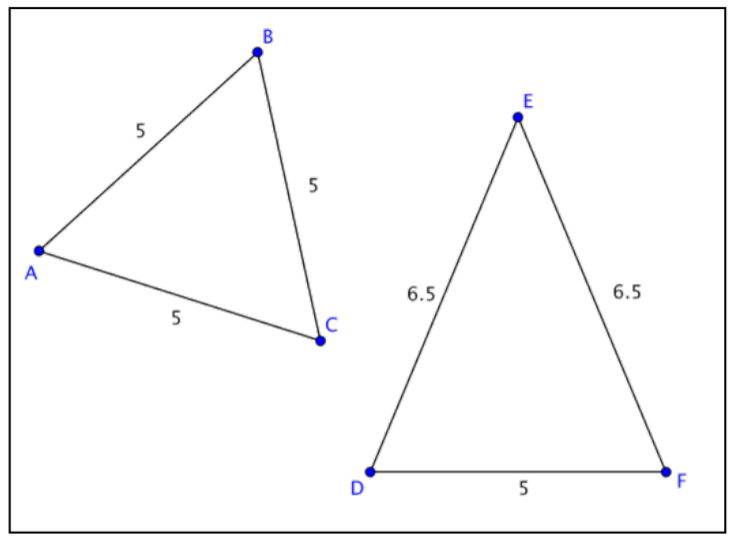
Determine whether the two triangles are similar, congruent, or neither.
Finding Missing Measurements in Similar Triangles
You can find the missing measurements in a triangle if you know some measurements of a similar triangle. Let’s look at an example.
∆ABC and ∆XYZ are similar triangles. What is the length of side BC?
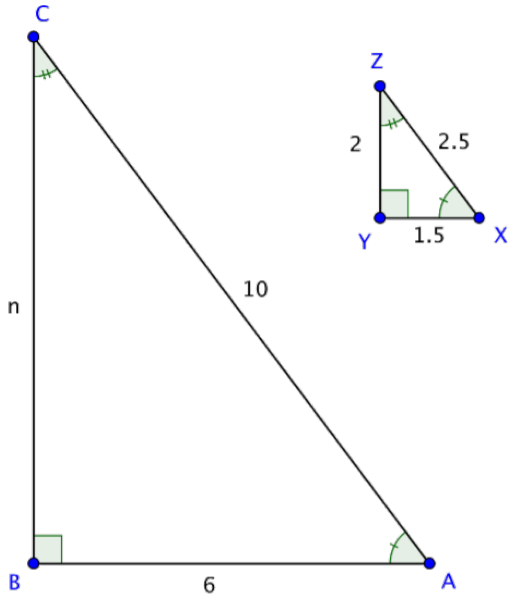
Solution
In similar triangles, the ratios of corresponding sides are proportional. Set up a proportion of two ratios, one that includes the missing side.
BCYZ=ABXY
Substitute in the known side lengths for the side names in the ratio. Let the unknown side length be n.
n2=61.5
Solve for n using cross multiplication.
2⋅6=1.5⋅n
12=1.5n
8=n
This process is fairly straightforward—but be careful that your ratios represent corresponding sides, recalling that corresponding sides are opposite corresponding angles.
Solving Application Problems Involving Similar Triangles
Applying knowledge of triangles, similarity, and congruence can be very useful for solving problems in real life. Just as you can solve for missing lengths of a triangle drawn on a page, you can use triangles to find unknown distances between locations or objects.
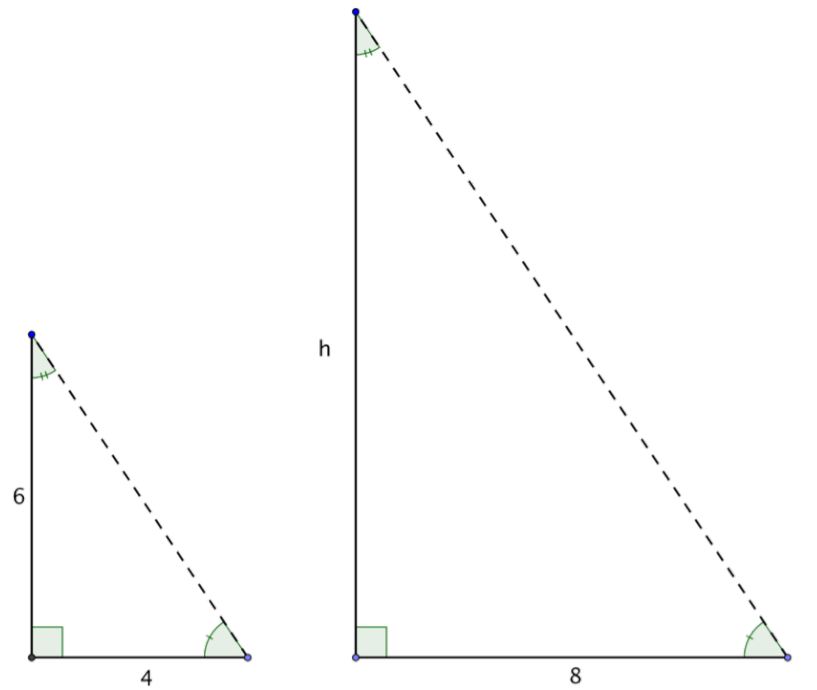
Let’s consider the example of two trees and their shadows. Suppose the sun is shining down on two trees, one that is 6 feet tall and the other whose height is unknown. By measuring the length of each shadow on the ground, you can use triangle similarity to find the unknown height of the second tree.
First, let’s figure out where the triangles are in this situation. The trees themselves create one pair of corresponding sides. The shadows cast on the ground are another pair of corresponding sides. The third side of these imaginary similar triangles runs from the top of each tree to the tip of its shadow on the ground. This is the hypotenuse of the triangle.
If you know that the trees and their shadows form similar triangles, you can set up a proportion to find the height of the tree.
When the sun is at a certain angle in the sky, a 6-foot tree will cast a 4-foot shadow. How tall is a tree that casts an 8-foot shadow?
Solution
The angle measurements are the same, so the triangles are similar triangles. Since they are similar triangles, you can use proportions to find the size of the missing side.
Tree 1Tree 2=Shadow 1Shadow 2
Set up a proportion comparing the heights of the trees and the lengths of their shadows.
Substitute in the known lengths. Call the missing tree height h.
6h=48
Solve for h using cross-multiplication.
6⋅8=4h
48=4h
12=h
Answer: The tree is 12 feet tall.
Summary
Triangles are one of the basic shapes in the real world. Triangles can be classified by the characteristics of their angles and sides, and triangles can be compared based on these characteristics. The sum of the measures of the interior angles of any triangle is 180º. Congruent triangles are triangles of the same size and shape. They have corresponding sides of equal length and corresponding angles of the same measurement. Similar triangles have the same shape, but not necessarily the same size. The lengths of their sides are proportional. Knowledge of triangles can be a helpful in solving real-world problems.
1. Obtuse scalene; this triangle has vertices P, Q, and R, one angle (angle Q) that is between 90º and 180º, and sides of three different lengths.
2. ∆ABC and ∆DEF are neither similar nor congruent; the corresponding angle measures are not known to be equal as shown by the absence of congruence marks on the angles. Also, the ratios of the corresponding sides are not equal: 6.55=6.55≠55
6.1.3: Pythagorean Theorem
- Use the Pythagorean Theorem to find the unknown side of a right triangle.
- Solve application problems involving the Pythagorean Theorem.
Introduction
A long time ago, a Greek mathematician named Pythagoras discovered an interesting property about right triangles: the sum of the squares of the lengths of each of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This property—which has many applications in science, art, engineering, and architecture—is now called the Pythagorean Theorem.
Let’s take a look at how this theorem can help you learn more about the construction of triangles. And the best part—you don’t even have to speak Greek to apply Pythagoras’ discovery.
The Pythagorean Theorem
Pythagoras studied right triangles, and the relationships between the legs and the hypotenuse of a right triangle, before deriving his theory.
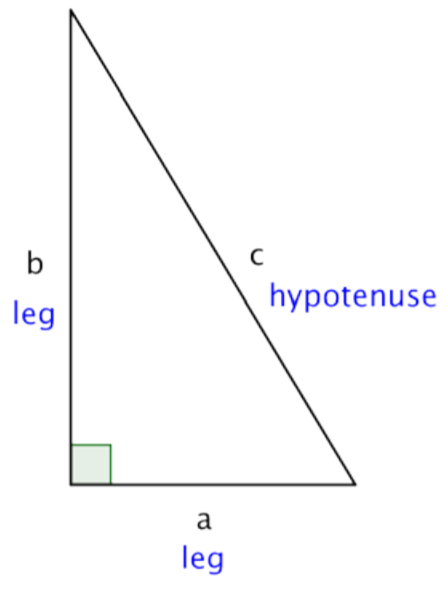
If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.
This relationship is represented by the formula: a2+b2=c2
In the box above, you may have noticed the word “square,” as well as the small 2s to the top right of the letters in a2+b2=c2. To square a number means to multiply it by itself. So, for example, to square the number 5 you multiply 5⋅5, and to square the number 12, you multiply 12⋅12. Some common squares are shown in the table below.
| Number | Number Times Itself | Square |
| 1 | 12=1⋅1 | 1 |
| 2 | 22=2⋅2 | 4 |
| 3 | 32=3⋅3 | 9 |
| 4 | 42=4⋅4 | 16 |
| 5 | 52=5⋅5 | 25 |
| 10 | 102=10⋅10 | 100 |
When you see the equation a2+b2=c2, you can think of this as “the length of side a times itself, plus the length of side b times itself is the same as the length of side c times itself.”
Let’s try out all of the Pythagorean Theorem with an actual right triangle.
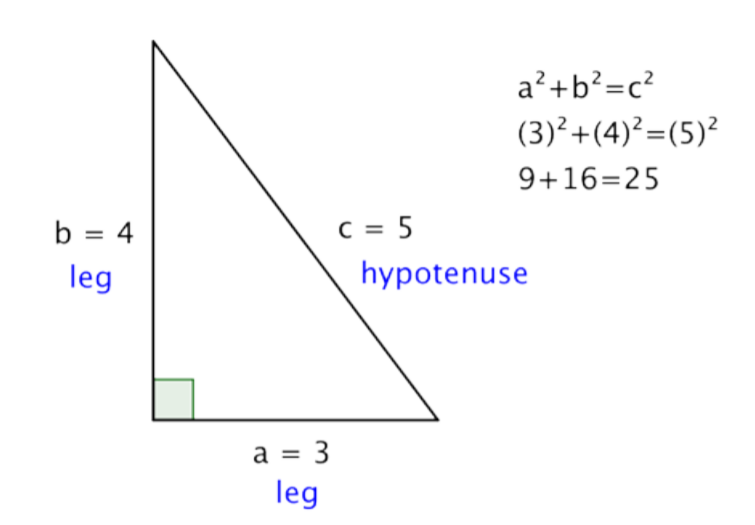
This theorem holds true for this right triangle—the sum of the squares of the lengths of both legs is the same as the square of the length of the hypotenuse. And, in fact, it holds true for all right triangles.
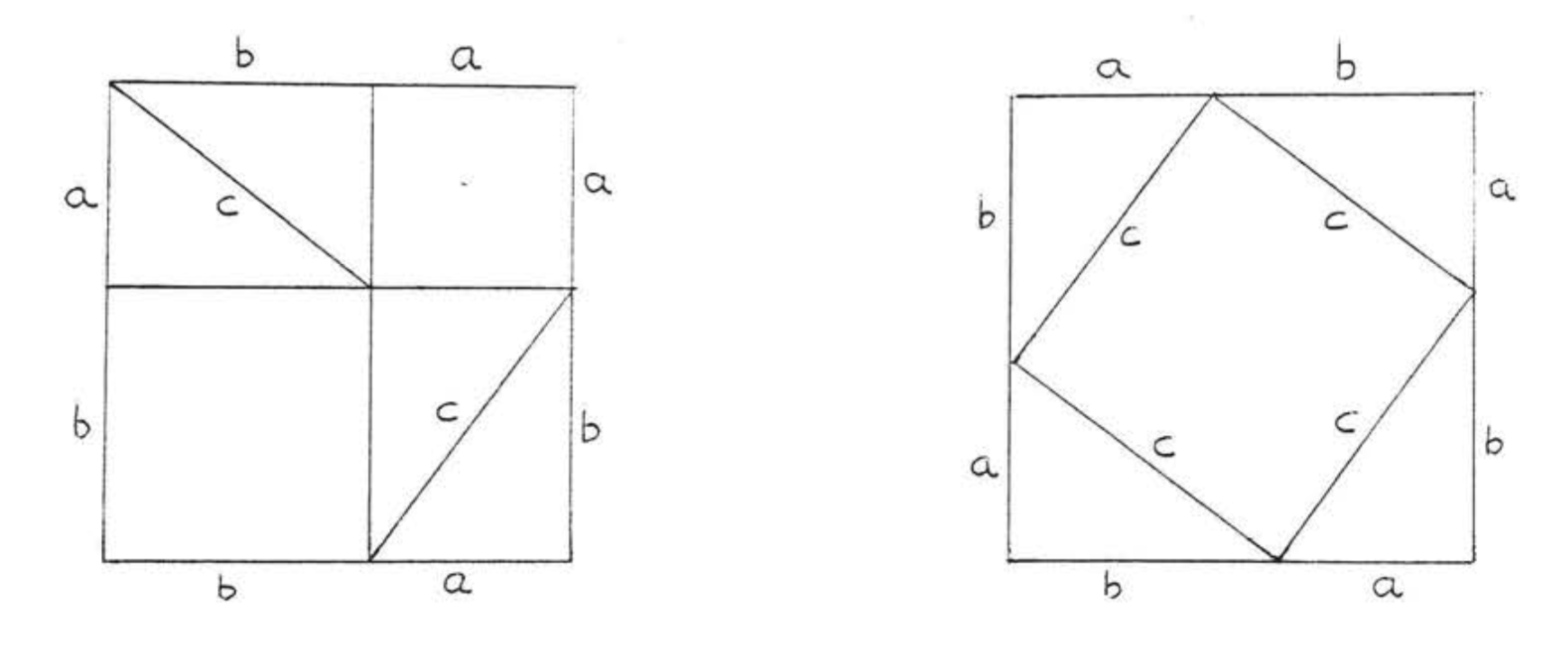
The Pythagorean Theorem can also be represented in terms of area. In any right triangle, the area of the square drawn from the hypotenuse is equal to the sum of the areas of the squares that are drawn from the two legs. You can see this illustrated below in the same 3-4-5 right triangle.
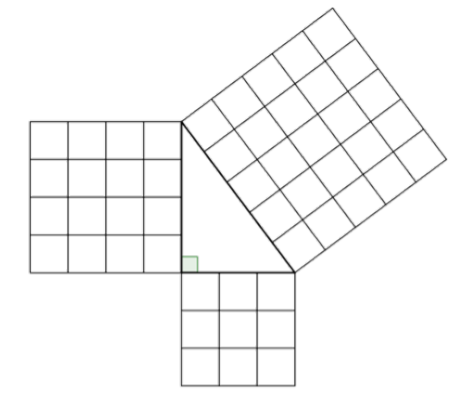
Note that the Pythagorean Theorem only works with right triangles.
Finding the Length of the Hypotenuse
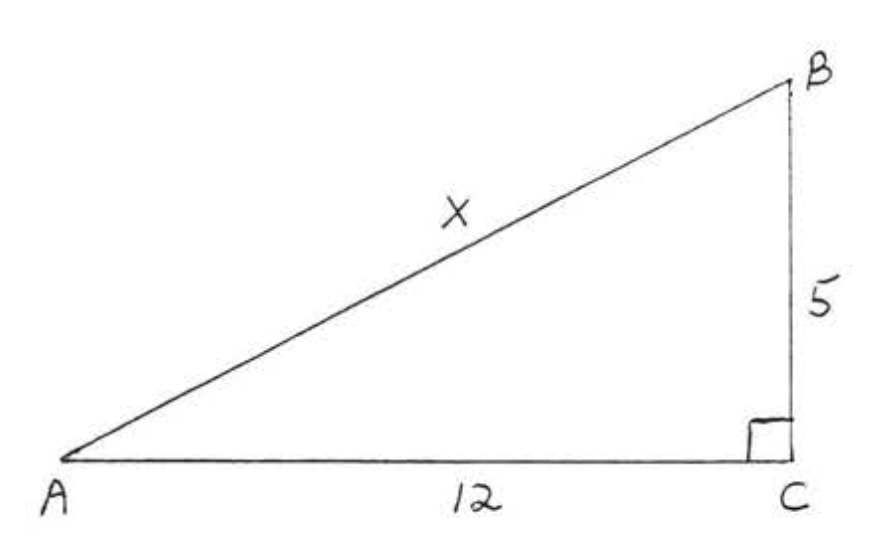
You can use the Pythagorean Theorem to find the length of the hypotenuse of a right triangle if you know the length of the triangle’s other two sides, called the legs. Put another way, if you know the lengths of a and b, you can find c.
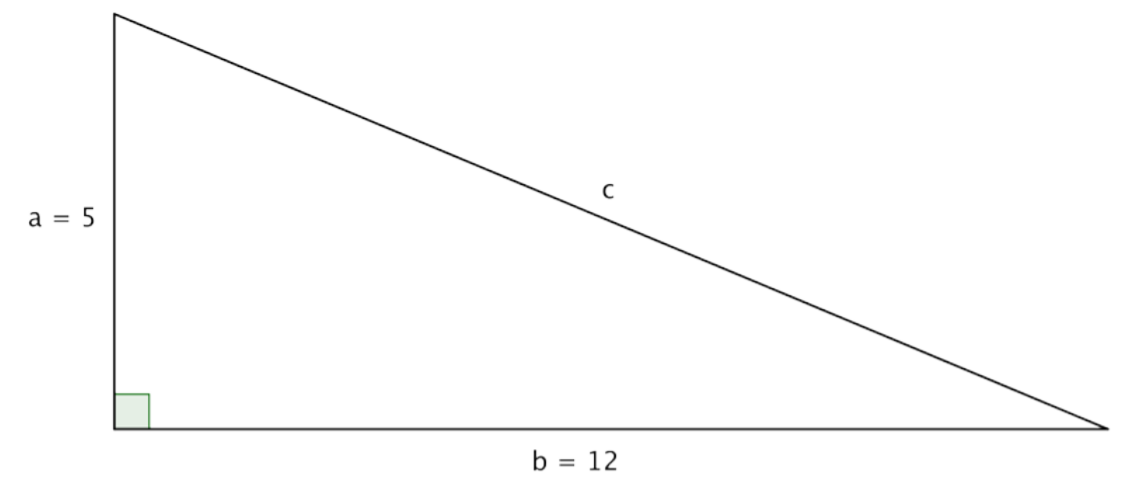
In the triangle above, you are given measures for legs a and b: 5 and 12, respectively. You can use the Pythagorean Theorem to find a value for the length of c, the hypotenuse.
The Pythagorean Theorem.
a2+b2=c2
Substitute known values for a and b.
(5)2+(12)2=c2
Evaluate.
25+144=c2
Simplify. To find the value of c, think about a number that, when multiplied by itself, equals 169. Does 10 work? How about 11? 12? 13? (You can use a calculator to multiply if the numbers are unfamiliar.)
169=c2
The square root of 169 is 13.
c=13
Using the formula, you find that the length of c, the hypotenuse, is 13.
In this case, you did not know the value of c—you were given the square of the length of the hypotenuse, and had to figure it out from there. When you are given an equation like 169=c2 and are asked to find the value of c, this is called finding the square root of a number. (Notice you found a number, c, whose square was 169.)
Finding a square root takes some practice, but it also takes knowledge of multiplication, division, and a little bit of trial and error. Look at the table below.
| Number x | Number y which, when multiplied by itself, equals number x | Square Root y |
| 1 | 1⋅1 | 1 |
| 4 | 2⋅2 | 2 |
| 9 | 3⋅3 | 3 |
| 16 | 4⋅4 | 4 |
| 25 | 5⋅5 | 5 |
| 100 | 10⋅10 | 10 |
It is a good habit to become familiar with the squares of the numbers from 0‒10, as these arise frequently in mathematics. If you can remember those square numbers—or if you can use a calculator to find them—then finding many common square roots will be just a matter of recall.
For which of these triangles is (3)2+(3)2=r2?
A) 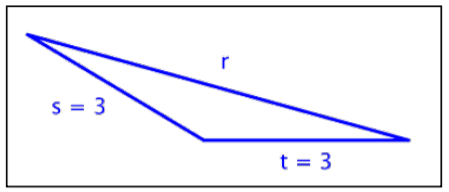 B)
B) 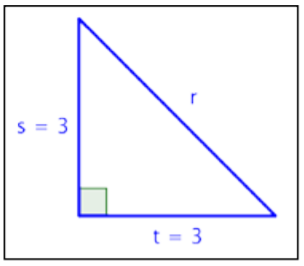
C) 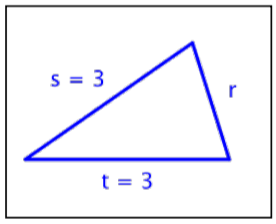 D)
D) 
Finding the Length of a Leg
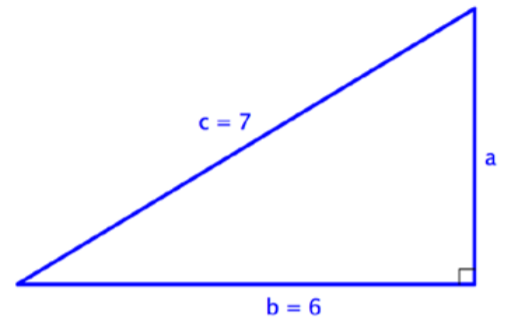
You can use the same formula to find the length of a right triangle’s leg if you are given measurements for the lengths of the hypotenuse and the other leg. Consider the example below.
Find the length of side a in the triangle below. Use a calculator to estimate the square root to one decimal place.
Solution
In this right triangle, you are given the measurements for the hypotenuse, c, and one leg, b. The hypotenuse is always opposite the right angle and it is always the longest side of the triangle.
a = ?
b = 6
c = 7
To find the length of leg a, substitute the known values into the Pythagorean Theorem.
a2+b2=c2
a2+62=72
Solve for a2. Think: what number, when added to 36, gives you 49?
a2+36=49
a2=13
Use a calculator to find the square root of 13. The calculator gives an answer of 3.6055…, which you can round to 3.6. (Since you are approximating, you use the symbol ≈.)
a≈3.6
Answer: a ≈ 3.6
Which of the following correctly uses the Pythagorean Theorem to find the missing side, x?
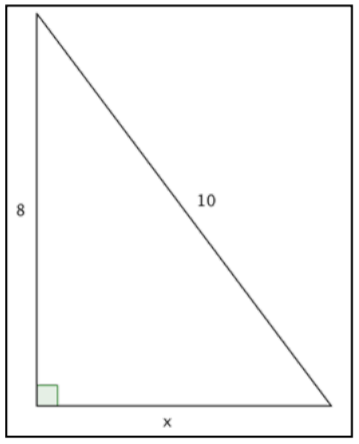
A) 82+102=x2
B) x+8=10
C) x2+82=102
D) x2+102=82
Using the Pythagorean Theorem to Solve Real-world Problems
The Pythagorean Theorem is perhaps one of the most useful formulas you will learn in mathematics because there are so many applications of it in real world settings. Architects and engineers use this formula extensively when building ramps, bridges, and buildings. Look at the following examples.
The owners of a house want to convert a stairway leading from the ground to their back porch into a ramp. The porch is 3 feet off the ground, and due to building regulations, the ramp must start 12 feet away from the base of the porch. How long will the ramp be?
Use a calculator to find the square root, and round the answer to the nearest tenth.
Solution
To solve a problem like this one, it often makes sense to draw a simple diagram showing where the legs and hypotenuse of the triangle lie.
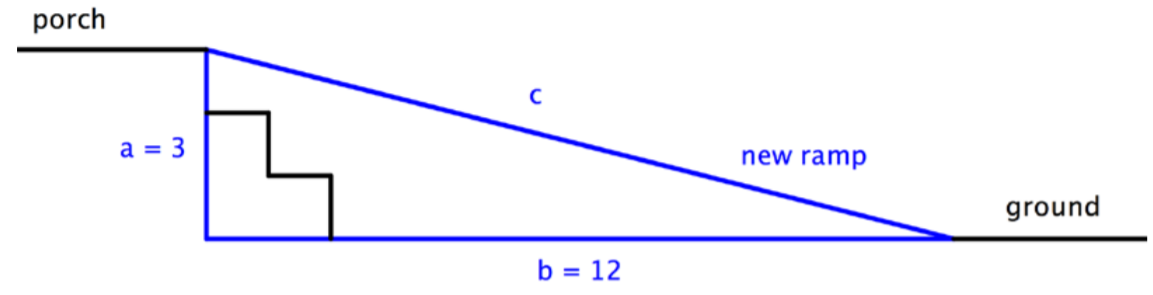
Identify the legs and the hypotenuse of the triangle. You know that the triangle is a right triangle since the ground and the raised portion of the porch are perpendicular—this means you can use the Pythagorean Theorem to solve this problem. Identify a, b, and c.
a = 3
b = 12
c = ?
Use the Pythagorean Theorem to find the length of c.
a2+b2=c2
32+122=c2
9+144=c2
153=c2
Use a calculator to find c.
12.4=c2
The square root of 153 is 12.369…, so you can round that to 12.4.
Answer: The ramp will be 12.4 feet long.
A sailboat has a large sail in the shape of a right triangle. The longest edge of the sail measures 17 yards, and the bottom edge of the sail is 8 yards. How tall is the sail?
Solution
Draw an image to help you visualize the problem. In a right triangle, the hypotenuse will always be the longest side, so here it must be 17 yards. The problem also tells you that the bottom edge of the triangle is 8 yards.

Setup the Pythagorean Theorem.
a2+b2=c2
a2+82=172
a2+64=289
a2=225
15⋅15=225, so
a=15
Answer: The height of the sail is 15 yards.
Summary
The Pythagorean Theorem states that in any right triangle, the sum of the squares of the lengths of the triangle’s legs is the same as the square of the length of the triangle’s hypotenuse. This theorem is represented by the formula 222 abc + = . Put simply, if you know the lengths of two sides of a right triangle, you can apply the Pythagorean Theorem to find the length of the third side. Remember, this theorem only works for right triangles.
1. B)  ; this is a right triangle; when you sum the squares of the lengths of the sides, you get the square of the length of the hypotenuse.
; this is a right triangle; when you sum the squares of the lengths of the sides, you get the square of the length of the hypotenuse.
2. C) x2+82=102; in this triangle, the hypotenuse has length 10, and the legs have length 8 and x. Substituting into the Pythagorean Theorem you have: x2+82=102; this equation is the same as x2+64=100, or x2=36. What number, times itself, equals 36? That would make x=6.
A triangle is formed when three straight line segments bound a portion of the plane. The line segments are called the sides of the triangle. A point where two sides meet is called a vertex of the triangle, and the angle formed is called an angle of the triangle. The symbol for triangle is △.
The triangle in Figure 2.3.1 is denoted by △ABC (or △BCA or △CAB, etc.).
- Its sides are AB, AC, and BC.
- Its vertices are A,B, and C.
- Its angles are ∠A, ∠B, and ∠C.
The triangle is the most important figure in plane geometry, This is because figures with more than three sides can always be divided into triangles (Figure 2.3.2). If we know the properties of a triangle, we can extend this knowledge to the study of other figures as well.
A fundamental property of triangles is the following:
The sum of the angles of a triangle is 180∘.
In △ABC of Figure 2.3.1, ∠A+∠B+∠C=180∘.
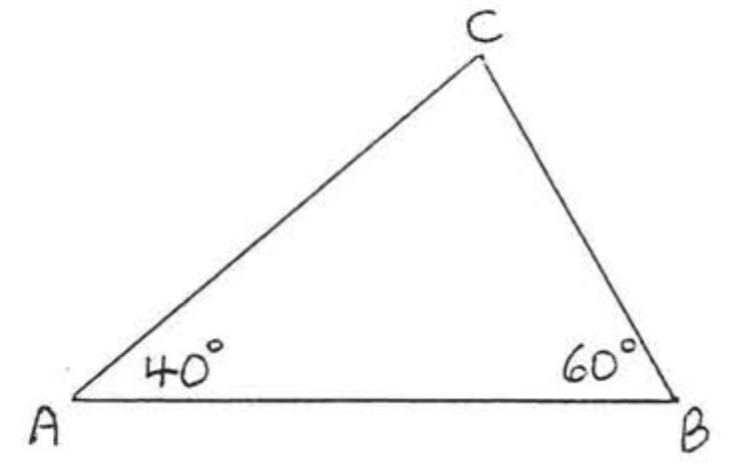
Find ∠C:
Solution
∠A+∠B+∠C=180∘40∘+60∘+∠C=180∘100∘+∠C=180∘∠C=180∘−100∘∠C=80∘
Answer: ∠C=80∘
Proof of Theorem 2.3.1: Through C draw DE parallel to AB (see Figure 2.3.3). Note that we are using the parallel postulate here, ∠1=∠A and ∠3=∠B because they are alternate interior angles of parallel lines, Therefore ∠A+∠B+∠C=∠1+∠3+∠2=180∘.

We may verify Theorem 2.3.1 by measuring the angles of a triangle with a protractor and taking the sum, However no measuring instrument is perfectly accurate, It is reasonable to expect an answer such as 179∘, 182∘, 180.5∘, etc. The purpose of our mathematical proof is to assure us that the sum of the angles of every triangle must be exactly \(180^{\circ}\).
Find x:

Solution
∠A+∠B+∠C=180∘2x+3x+4x=1809x=180x=20
Check:

Answer: x=20.
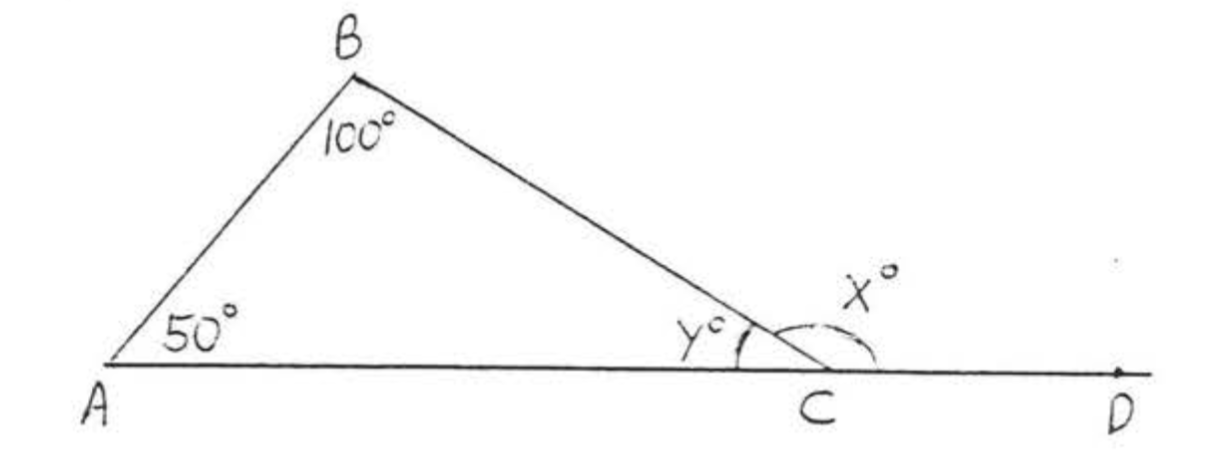
Find y and x:
Solution
50+100+y=180150+y=180y=180−150y=30x=180−30=150
Answer: y=30, x=150.
In Figure 2.3.4, ∠x is called an exterior angle of △ABC, ∠A, ∠B, and ∠y are called the interior angles of △ABC. ∠A and ∠B are said to be the interior angles remote from the exterior angle ∠x.
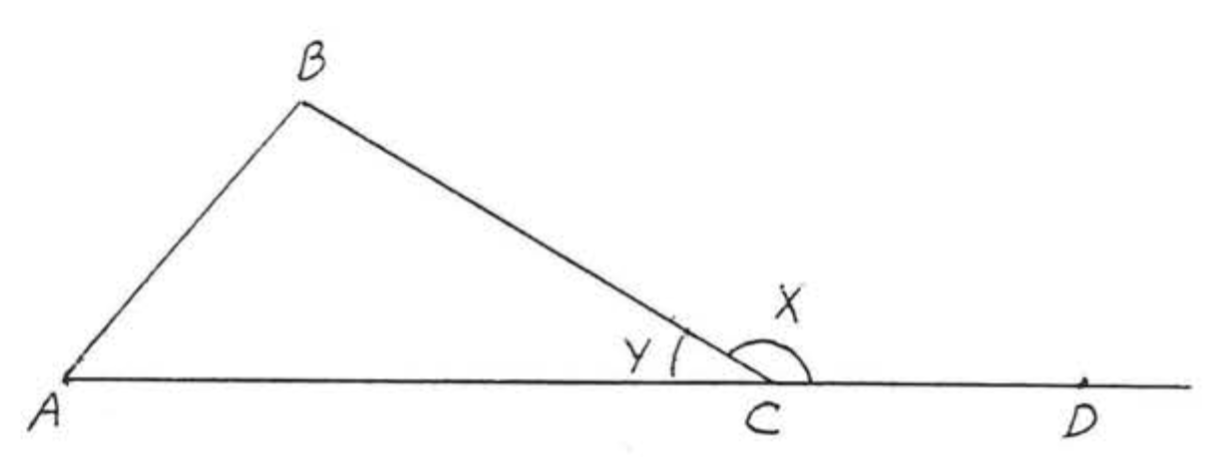
The results of Example 2.3.3 suggest the following theorem.
An exterior angle is equal to the sum of the two remote interior angles,
In Figure 2.3.4, ∠x=∠A+∠B.
Find x:

Solution
Using Theorem 2.3.2, x∘=100∘+50∘=150∘.
Answer: x=150.
Proof of Theorem 2.3.2: We present this proof in double-column form, with statements in the left column and the reason for each statement in the right column. The last statement is the theorem we wish to prove.
| Statements | Reasons |
| 1. ∠A+∠B+∠y=180∘ | 1. The sum of the angles of a triangle is 180∘. |
| 2. ∠A+∠B=180∘−∠y | 2. Subtract ∠y from both sides of the equation, statement 1. |
| 3. ∠x=180∘−∠y. | 3. ∠x and ∠y are supplementary. |
| 4. ∠x=∠A+∠B. | 4. Both ∠x (statement 3) and ∠A+∠B (statement 2) equal 180∘−∠y. |
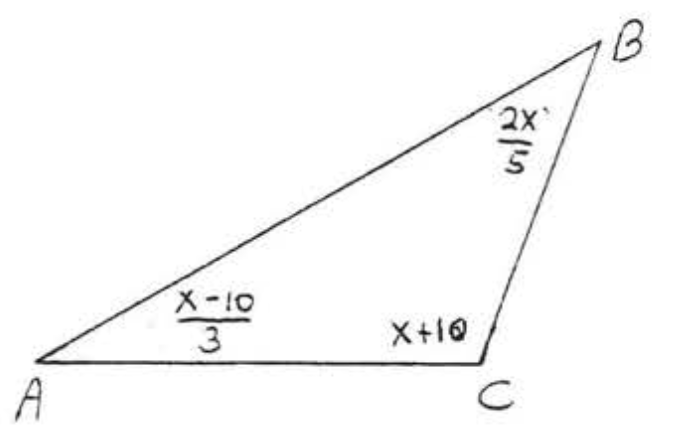
Find x:
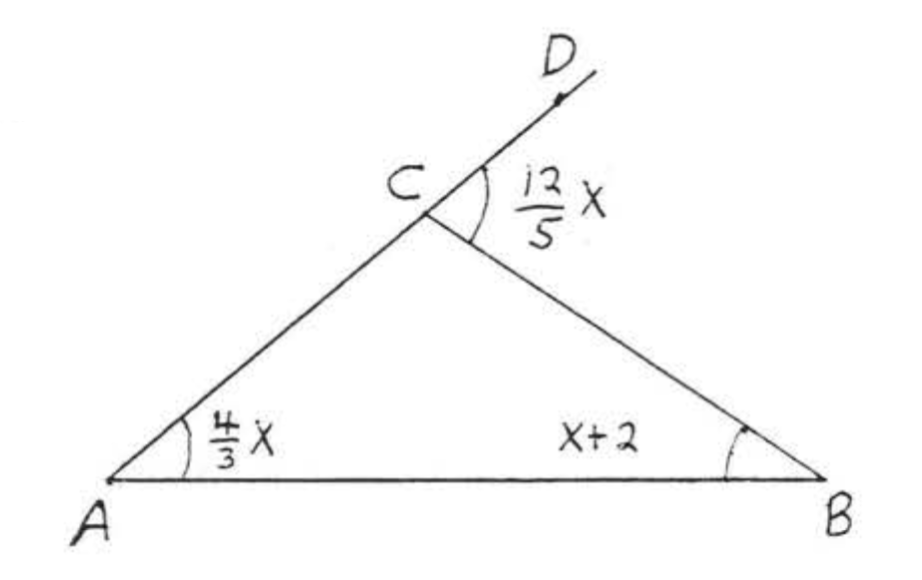
Solution
∠BCD is an exterior angle with remote interior angles ∠A and ∠B. By Theorem 2.3.2,
∠BCD=∠A+∠B125x=43x+x+2
The least common denominator (1, c, d) is 15.
3(15)125x=3(15)43x+(15)x+(15)(2)36x=20x+15x+3036x=35x+3036x−35x=30x=30
Check:
Answer: x=30.
Our work on the sum of the angles of a triangle can easily be extended to other figures:
Find the sum of the angles of a quadrilateral (four sided figure),
Solution
Divide the quadrilateral into two triangles as illustrated,
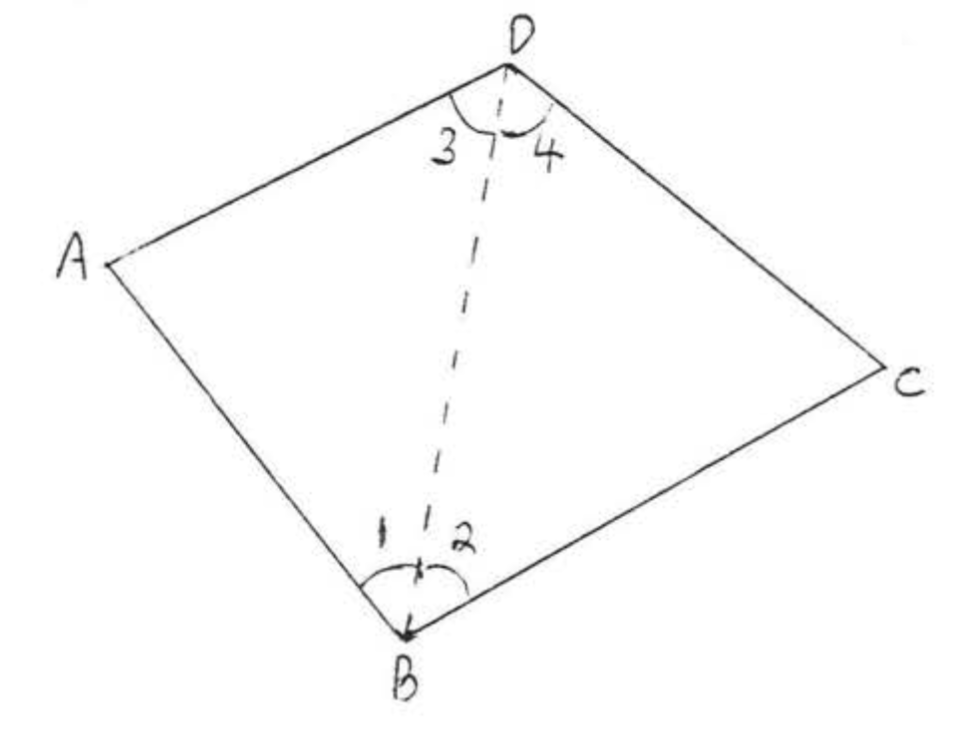
∠A+∠B+∠C+∠D=∠A+∠1+∠3+∠2+∠4+∠C=180∘+180∘=360∘
Answer: 360∘.
Find the sum of the angles of a pentagon (five-sided figure).
Solution
Divide the pentagon into three triangles as illustrated, The sum is equal to the sum of the angles of the three triangle = (3)(180∘)=540∘.
Answer: 540∘.
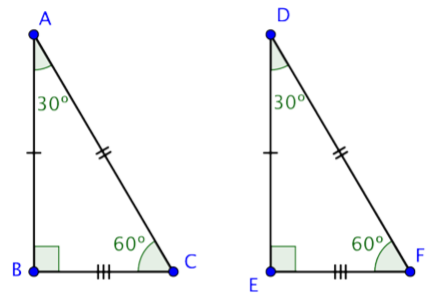
There is one more simple principle which we will derive from Theorem 2.3.1, Consider the two triangles in Figure 2.3.5.

We are given that ∠A=∠D=60∘ and ∠B=∠E=40∘. A short calculation shows that we must also have ∠C=∠F=80∘. This suggests the following theorem:
If two angles of one triangle are equal respectively to two angles of another triangle, then their remaining angles are also equal.
In Figure 2.3.6, if ∠A=∠D and ∠B=∠E then ∠C=∠F.
- Proof
-
∠C=180∘−(∠A+∠B)=180∘−(∠D+∠E)=∠F.

Figure 2.3.6. ∠A=∠D and ∠B=∠E.
Our Theorem 2.3.1, which states that the sum of the angles of a triangle is 180∘, is one of the most important consequences of the parallel postulate, Therefore, one way of testing the truth of the parallel postulate (see the Historical Note in Section 1.4) is to test the truth of Theorem 2.3.1, This was actually tried by the German mathematician, astronomer, and physicist, Karl Friedrich Gauss (1777 - 1855). (This is the same Gauss whose name is used as a unit of measurement in the theory of magnetism), Gauss measured the sum of the angles of the triangle formed by three mountain peaks in Germany, He found the sum of the angles to be 14.85 seconds more than 180∘ (60 seconds 1 minute, 60 minutes = 1 degree). However this small excess could have been due to experimental error, so the sum might actually have been 180∘.
Aside from experimental error, there is another difficulty involved in verifying the angle sum theorem. According to the non-Euclidean geometry of Lobachevsky, the sum of the angles of a triangle is always less than 180∘. In the non-Euclidean geometry of Riemann, the sum of the angles is always more than 180∘, However in both cases the difference from 180∘ is insignificant unless the triangle is very large, Neither theory tells us exactly how large such a triangle should be, Even if we measured the angles of a very large triangle, like one formed by three stars, and found the sum to be indistinguishable from 180∘, we could only say that the angle sum theorem and parallel postulate are apparently true for these large distances, These distances still might be too small to enable us to determine whichgeometric system best describes the universe as a whole,
Problems
1 - 12. Find x and all the missing angles of each triangle:
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 
13 - 14. Find x,y, and z:
13.  14.
14. 
15 - 20. Find x:
15.  16.
16. 
17.  18.
18. 
19.  20.
20. 
21. Find the sum of the angles of a hexagon (6-sided figure).
22. Find the sum of the angles of an octagon (8-sided figure).
23 - 26. Find x:
23.  24.
24. 
25.  26.
26. 
In a right triangle, the sides of the right angle are called the legs of the triangle and the remaining side is called the hypotenuse. In Figure 2.3.1, side AC and BC are the legs and side AB is the hypotenuse.
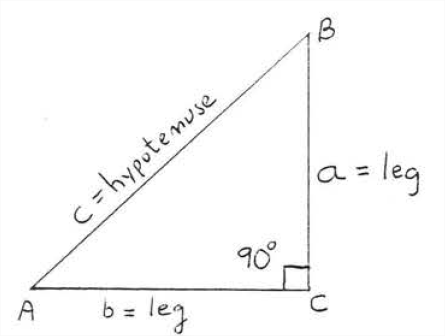
The following is one of the most famous theorems in mathematics.
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. That is,
leg2+leg2=hypotenuse2
Thus, for the sides of the triangle in Figure 2.3.1,
a2+b2=c2
Before we prove Theorem 2.3.1, we will give several examples.
Find x
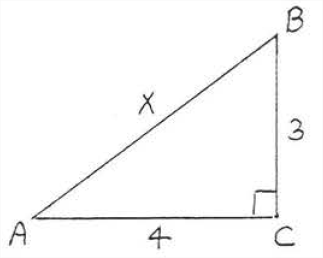
Solution
leg2+leg2=hyp232+42=x29+16=x225=x25=x
Check:
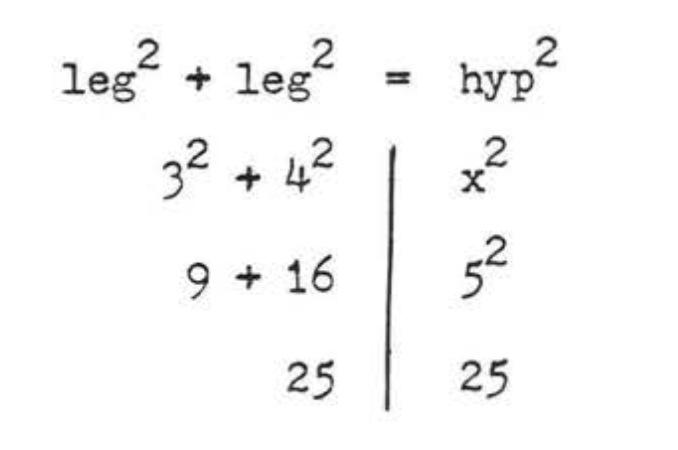
Answer: x=5.
Find x:
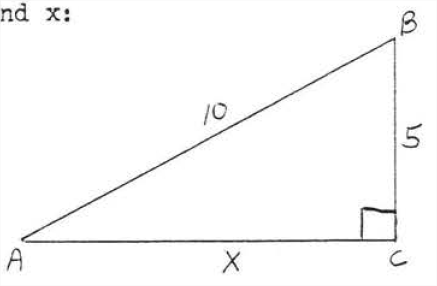
Solution
leg2+leg2=hyp252+x2=10225+x2=100x2=75x=√75=√25√3=5√3
Check:
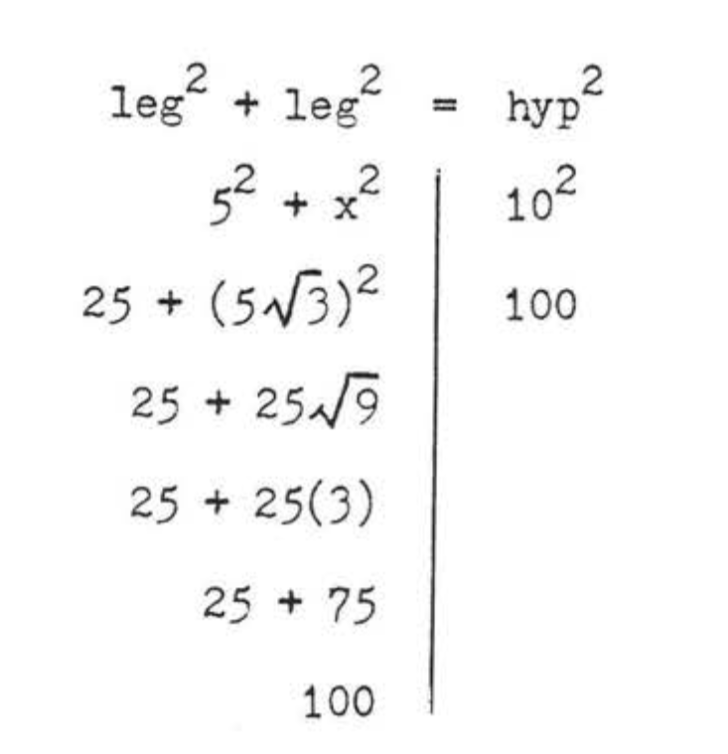
Answer: x=5√3.
Find x:
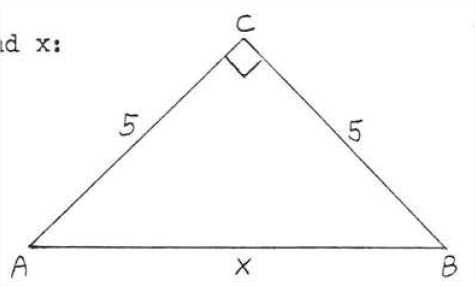
Solution
leg2+leg2=hyp252+52=x225+25=x250=x2x=√50=√25√2=5√2
Check:
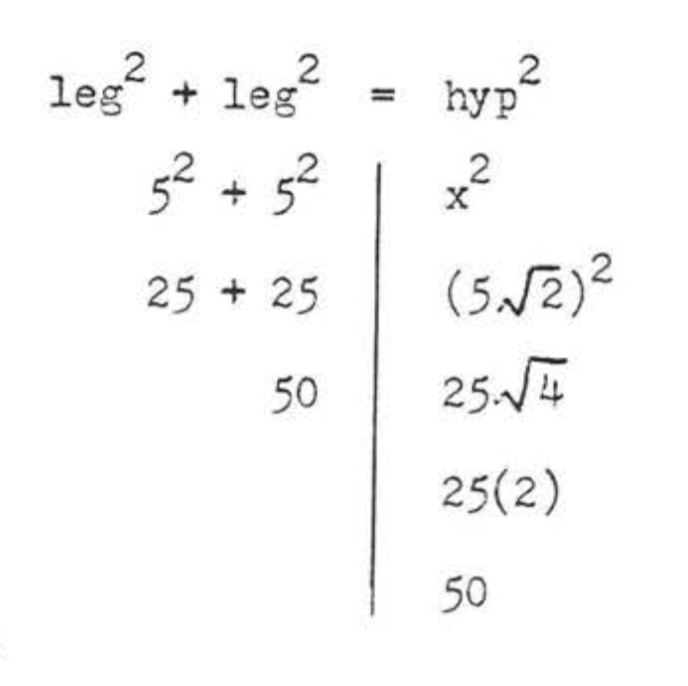
Answer: x=5√2.
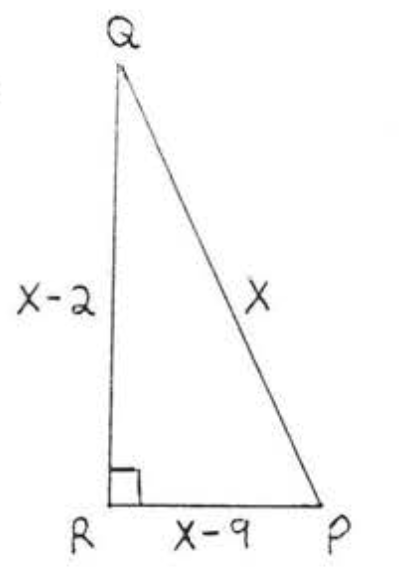
Find x
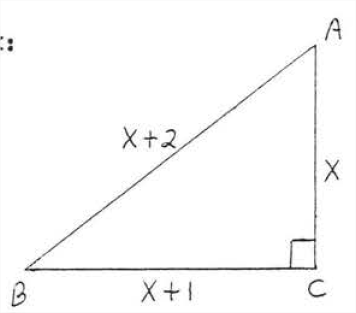
Solution
leg2+leg2=hyp2x2+(x+1)2=(x+2)2x2+x2+2x+1=x2+4x+4x2+x2+2x+1−x2−4x−4=0x2−2x−3=0(x−3)(x+1)=0
x−3=0x=3 x+1=0x=−1
We reject x=−1 because AC=x cannot be negative.
Check, x=3:
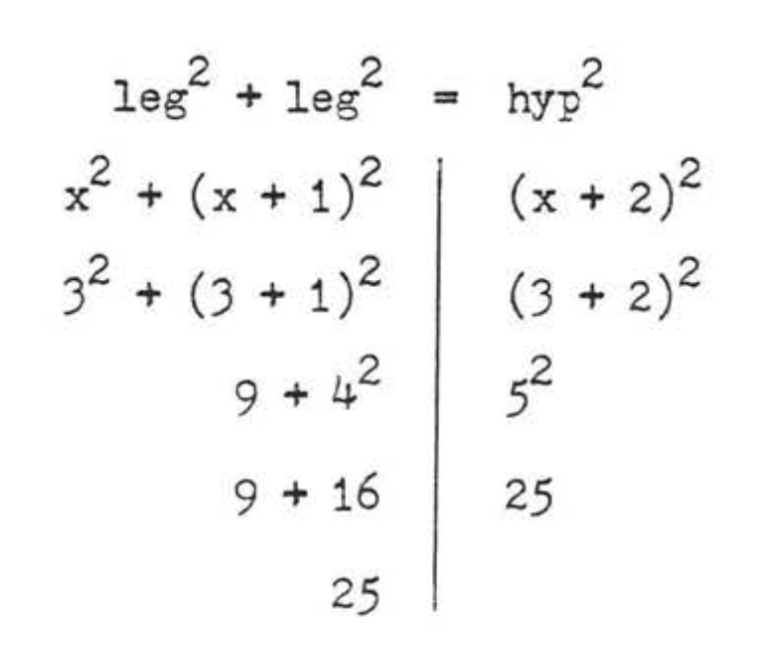
Answer: x=3.
We will now restate and prove Theorem 2.3.1:
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs. That is,
leg2+leg2=hypotenuse2.
In Figure 2.3.1,
a2+b2=c2.
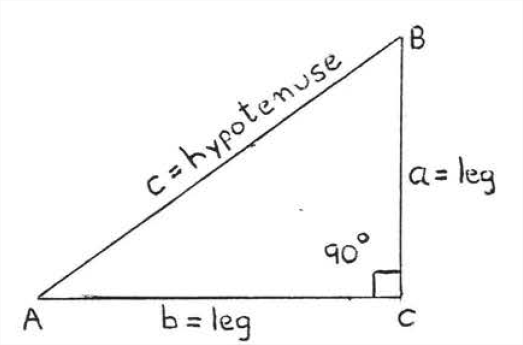

- Proof
-
In Figure 2.3.1, draw CD perpendicular to AB. Let x=AD. Then BD=c−x (Figure 2.3.2). As in Example 2.3.3, section 4.2, △ABC∼△ACD and △ABC∼△CBD. From these two similarities we obtain two proportions:

The converse of the Pythagorean Theorem also holds:
In a triangle, if the square of one side is equal to the sun of the squares of the other two sides then the triangle is a right triangle.
In Figure 2.3.3, if c2=a2+b2 then △ABC is a right triangle with ∠C=90∘.
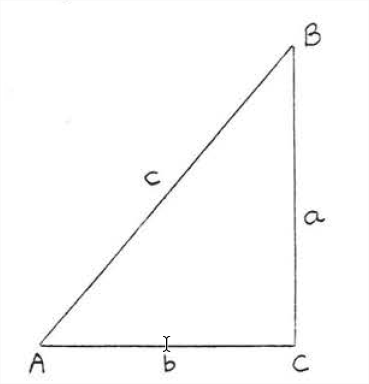
- Proof
-
Draw a new triangle, △DEF, so that ∠F=90∘, d=a, and e=b (Figure 2.3.4). △DEF is a right triangle, so by Theorem 2.3.1, f2=d2+e2. We have f2=d2+e2=a2+b2=c2 and therefore f=c. Therefore △ABC≅△DEF because SSS=SSS. Therefore, ∠C+∠F=90∘.

Figure 2.3.4: Given △ABC, draw △DEF so that ∠F=90∘, d=a and e=b.
Is △ABC a right triangle?

Solution
AC2=72=49
BC2=92=81
AB2=(√130)2=130
49+81=130.
so by Theorem 2.3.2, △ABC is a right triangle.
Answer: yes.
Find x and AB:
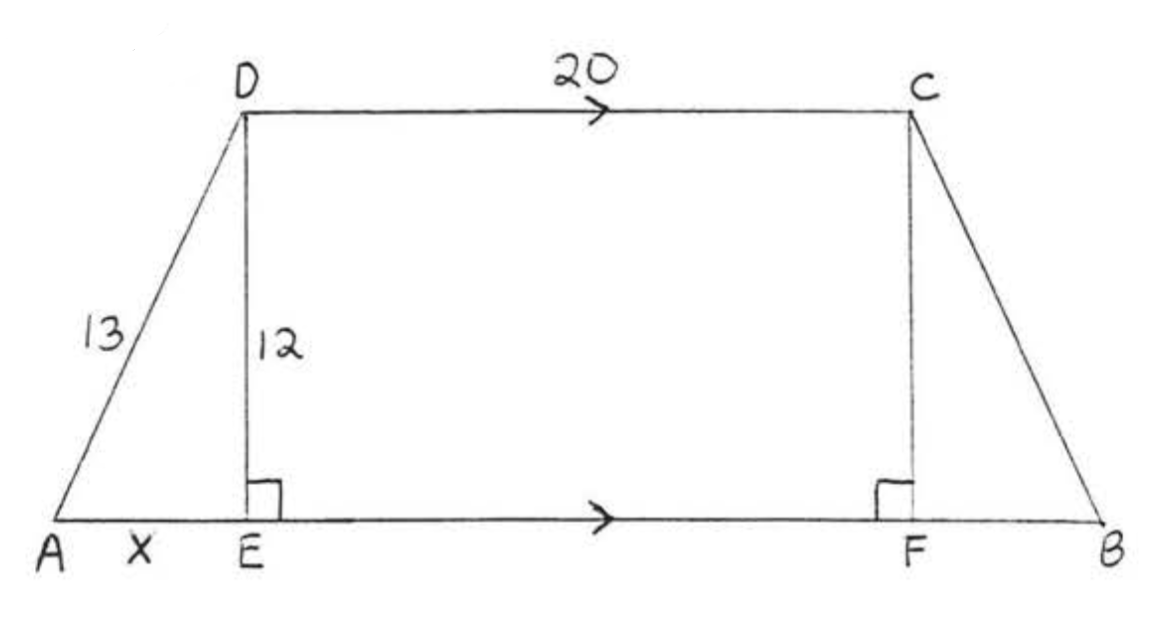
Solution
x2+122=132x2+144=169x2=169−144x2=25x=5
CDEF is a rectangle so EF=CD=20 and CF=DE=12. Therefore FB=5 and AB=AE+EF+FB=5+20+5=30.
Answer: x=5, AB=30.
Find x, AC and BD:
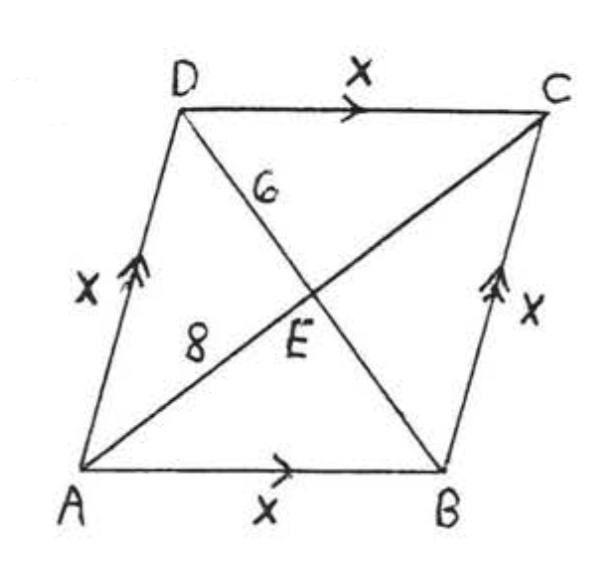
Solution
ABCD is a rhombus. The diagonals of a rhombus are perpendicular and bisect each other.
62+82=x236+64=x2100=x210=x
AC=8+8=16,BD=6+6=12.
Answer: x=10,AC=16,BD=12.
A ladder 39 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 15 feet from the building?

Solution
leg2+leg2=hyp2x2+152=392x2+225=1521x2=1521−225x2=1296x=√1296=36
Answer: 36 feet.
Pythagoras (c. 582 - 507 B.C.) was not the first to discover the theorem which bears his name. It was known long before his time by the Chinese, the Babylonians, and perhaps also the Egyptians and the Hindus, According to tradition, Pythagoras was the first to give a nroof of the theorem, His proof probably made use of areas, like the one suggested. In Figure 2.3.5 below, (each square contains four congruent right triangles with sides of lengths a, b, and c, In addition the square on the left contains a square with side a and a square with side b while the one on the right contains a square with side c.)
um theorem for triangles, the properties of parallel lines, and the theory of similar triangles and proportions.
Problems
1 - 10. Find x. Leave answers in simplest radical form.
1.

2.
3.

4.

5.

6.
7.

8.

9.

10.

11 - 14. Find x and all sides of the triangle:
11.

12.

13.
14.

15 - 16. Find x:
15.

16.

17. Find x and AB.

18. Find x:

19. Find x,AC and BD:

20. Find x,AC and BD:

21. Find x and y:

22. Find x, AC and BD:

23. Find x,AB and BD:
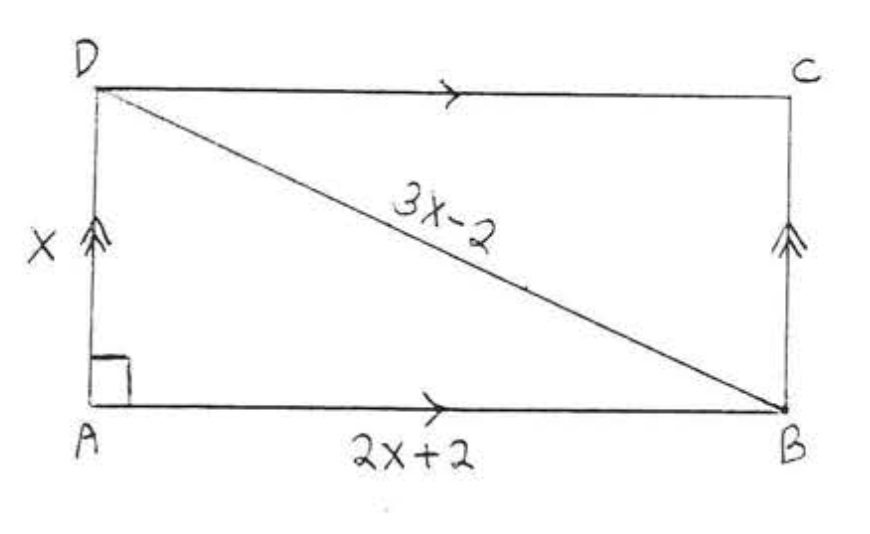
24. Find x,AB and AD:

25 - 30. Is △ABC a right triangle?
25.

26.
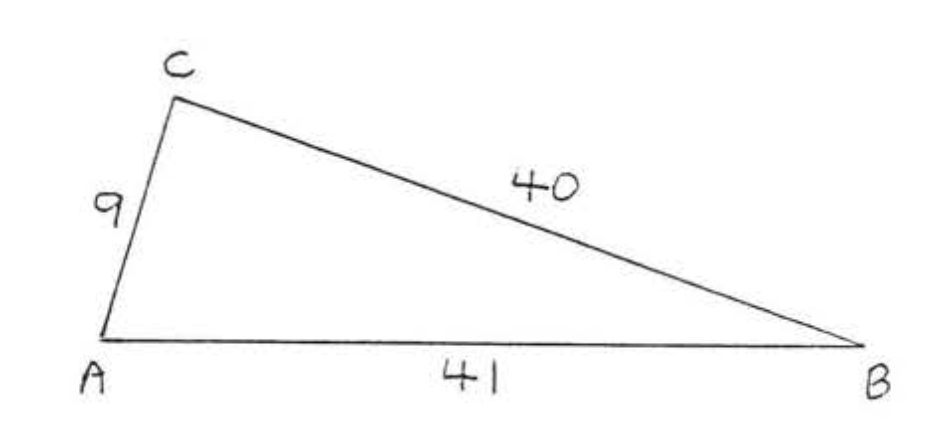
27.
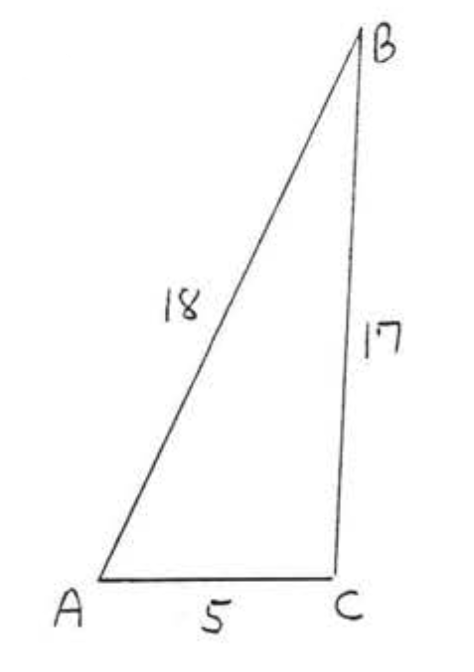
28.
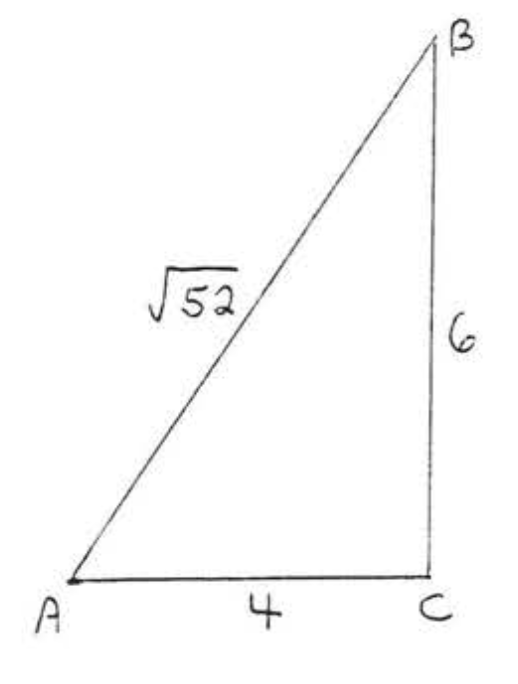
29.

30.

31. A ladder 25 feet long leans against a building, How far up the side of the building does the ladder reach if the foot of the ladder is 7 feet from the building?
32. A man travels 24 miles east and then 10 miles north. At the end of his journey how far is he from his starting point?
33. Can a table 9 feet wide (with its legs folded) fit through a rectangular doorway 4 feet by 8 feet?
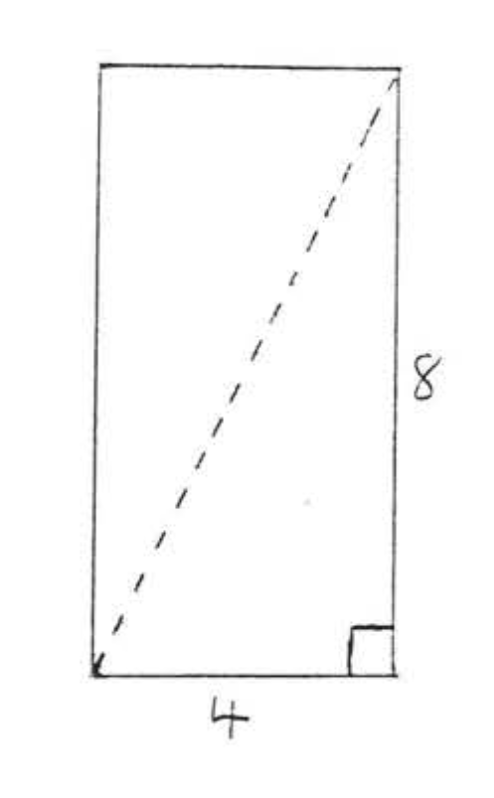
34. A baseball diamond is a square 90 feet on each side, Find the distance from home plate to second base (leave answer in simplest radical form).

This appendix contains some formulas and results from geometry that are important in the study of trigonometry.
For a circle with radius r:
- Circumference: C=2πr
- Area: A=πr2

- The sum of the measures of the three angles of a triangle is 180∘.
- A triangle in which each angle has a measure of less that 90∘ is called an acute triangle.
- A triangle that has an angle whose measure is greater than 90∘ is called an obtuse triangle.
- A triangle that contains an angle whose measure is 90∘ is called a right triangle. The side of a right triangle that is opposite the right angle is called the hypotenuse, and the other two sides are called the legs.
- An isosceles triangle is a triangle in which two sides of the triangle have equal length. In this case, the two angles across from the two sides of equal length have equal measure.
- An equilateral triangle is a triangle in which all three sides have the same length. Each angle of an equilateral triangle has a measure of 60∘.
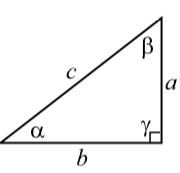
- The sum of the measures of the two acute angles of a right triangle is 90∘. In the diagram on the right, α+β=90∘.
- The Pythagorean Theorem. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. In the diagram on the right, c2=a2+b2
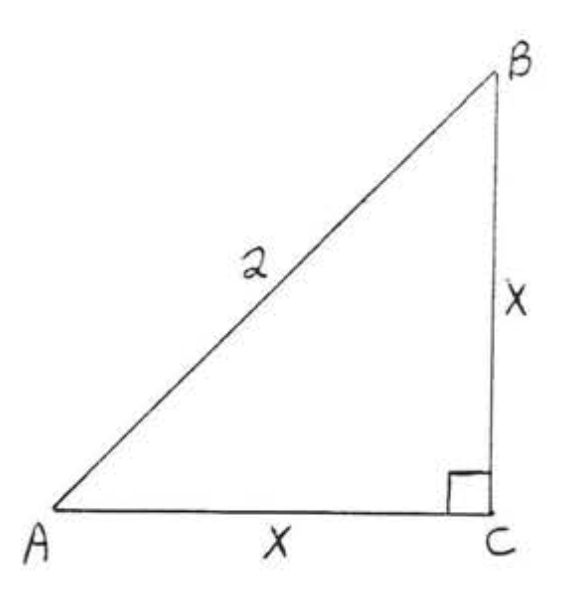
A right triangle in which both acute angles are 45∘. For this type of right triangle, the lengths of the two legs are equal. So if c is the length of the hypotenuse and x is the length of each of the legs, then by the Pythagorean Theorem, c2=x2+x2. Solving this equation for x, we obtain
2x2=c2
x2=c22
x=√c22
x=x√2=c√22

A right triangle with acute angles of 30∘ and 60∘.
We start with an equilateral triangle with sides of length c. By drawing an angle bisector at one of the vertices, we create two congruent right triangles with acute angles of 30∘ and 60∘.

This means that the third side of each of these right triangles will have a length of c2. If the length of the altitude is x, then using the Pythagorean Theorem, we obtain
c2=x2+(c2)2
x2=c2−c24
x2=3c24
x=√3c24=c√32
Two triangles are similar if the three angles of one triangle are equal in measure to the three angles of the other triangle. The following diagram shows similar triangles △ABC and △DEF. We write △ABC∼△DEF.

The sides of similar triangles do not have to have the same length but they will be proportional. Using the notation in the diagram, this means that
ad=be=cf
We use some properties of parallelograms in the study of vectors in Section 3.5. A parallelogram is a quadrilateral with two pairs of parallel sides. We will use the diagram on the right to describe some properties of parallelograms.
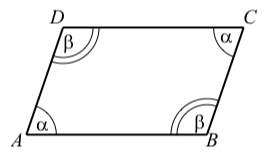
- Opposite sides are equal in length. In the diagram, this means that AB=DC and AD=BC
- As shown in the diagram, opposite angles are equal. That is, ∠DAB=∠BCD and ∠ABC=∠CDA
- The sum of two adjacent angles is 180∘. In the diagram, this means that α+β=180∘


