2.2: Geometrical Shapes

Last updated
Save as PDF

Page ID: 76284

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

know what a polygon is
know what perimeter is and how to find it
know what the circumference, diameter, and radius of a circle is and how to find each one
know the meaning of the symbol ππ and its approximating value
know what a formula is and four versions of the circumference formula of a circle
know the meaning and notation for area
know the area formulas for some common geometric figures
be able to find the areas of some common geometric figures
know the meaning and notation for volume
know the volume formulas for some common geometric objects
be able to find the volume of some common geometric objects

Polygons

We can make use of conversion skills with denominate numbers to make measurements of geometric figures such as rectangles, triangles, and circles. To make these measurements we need to be familiar with several definitions.

Definition: Polygon

A polygon is a closed plane (flat) figure whose sides are line segments (portions of straight lines).

Polygons

$Four shapes, each completely closed, with various numbers of straight line segments as sides.$

Not polygons

$Four shapes. One three-sided open box. One oval. One oval-shaped object with one flat side, and one nondescript blob.$

Perimeter

Definition: Perimeter

The perimeter of a polygon is the distance around the polygon.

To find the perimeter of a polygon, we simply add up the lengths of all the sides.

Sample Set A

Find the perimeter of each polygon.

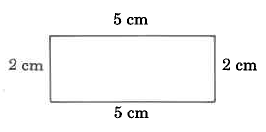
$A rectangle with short sides of length 2 cm and long sides of length 5 cm.$

Solution

$\begin{array} {rcl} {\text{Perimeter}} & = & {\text{2 cm + 5 cm + 2 cm + 5 cm}} \\ {} & = & {\text{14 cm}} \end{array}$

Sample Set A

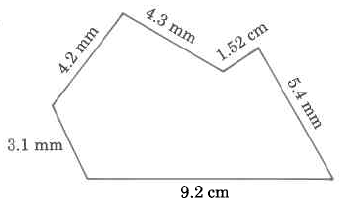
$A polygon with sides of the following lengths: 9.2cm, 31mm, 4.2mm, 4.3mm, 1.52cm, and 5.4mm.$

Solution

$\begin{array} {rcr} {\text{Perimeter}} & = & {\text{3.1 mm}} \\ {} & & {\text{4.2 mm}} \\ {} & & {\text{4.3 mm}} \\ {} & & {\text{1.52 mm}} \\ {} & & {\text{5.4 mm}} \\ {} & & {\underline{\text{+ 9.2 mm}}} \\ {} & & {\text{27.72 mm}} \end{array}$

Sample Set A

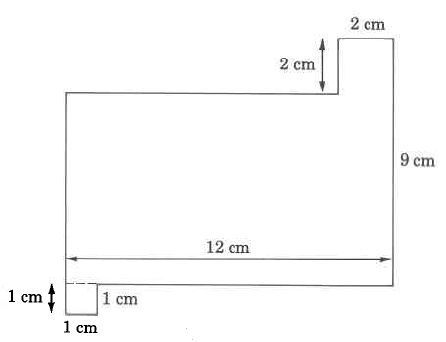
$A polygon with eight sides. It is not an octagon, but can be visualized as one large rectangle with two smaller rectangles connected to it.$

Solution

Our first observation is that three of the dimensions are missing. However, we can determine the missing measurements using the following process. Let A, B, and C represent the missing measurements. Visualize

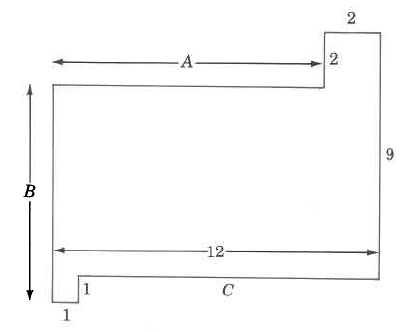
$A polygon with eight sides. It is not an octagon, but can be visualized as one large rectangle with two smaller rectangles connected to it. The height and width are measured and labeled with variables, A, B, and C.$

$\text{A = 12m - 2m = 10m}$
$\text{B = 9m + 1m - 2m = 8m}$
$\text{C = 12m - 1m = 11m}$

$\begin{array} {rcr} {\text{Perimeter}} & = & {\text{8 m}} \\ {} & & {\text{10 m}} \\ {} & & {\text{2 m}} \\ {} & & {\text{2 m}} \\ {} & & {\text{9 m}} \\ {} & & {\text{11 m}} \\ {} & & {\text{1 m}} \\ {} & & {\underline{\text{+ 1 m}}} \\ {} & & {\text{44 m}} \end{array}$

Practice Set A

Find the perimeter of each polygon.

$A three-sided polygon with sides of the following lengths: 3 ft, 8 ft, and 9 ft.$

Answer: 20 ft

Practice Set A

$A four-sided polygon with sides of the following length: 6.1m, 8.6m, 6.3m, and 5.8m.$

Answer: 26.8 m

Practice Set A

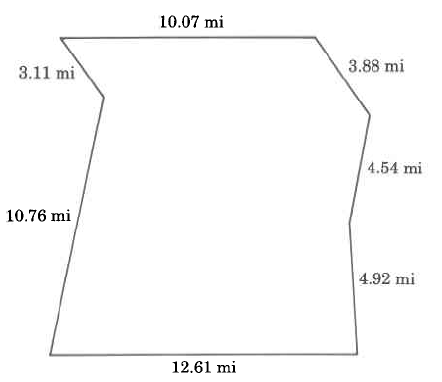
$A seven-sided polygon with sides of the following lengths: 10.07mi, 3.88mi, 4.54mi, 4.92mi, 12.61, 10.76mi, and 3.11mi.$

Answer: 49.89 mi

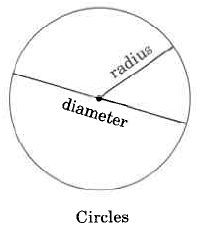
Circumference/Diameter/Radius

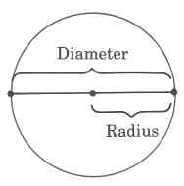
Diameter (d)
A diameter of a circle is any line segment that passes through the center of the circle and has its endpoints on the circle.

Radius (r)
A radius of a circle is any line segment having as its endpoints the center of the circle and a point on the circle.
The radius is one half the diameter.

Circumference (C)
The circumference of a circle is the distance around the circle. It is given by $C = \pi d= 2 \pi r$
$A circle with a line directly through the middle, ending at the edges of the shape. The entire length of the line is labeled diameter, and the length of the portion of the line from the center of the circle to the edge of the circle is labeled radius.$

Sample Set B

Find the circumference of the circle.

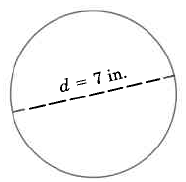
$A circle with a dashed line from one edge to the other, labeled d = 7 in.$

Solution

Use the formula $C = \pi d$.

$C = \pi \cdot 7\ in.$

By commutativity of multiplication,

$C = 7\ in. \cdot \pi$

$C = 7 \pi in.$, exactly

This result is exact since $\pi$ has not been approximated.

Sample Set B

Find the perimeter of the figure.

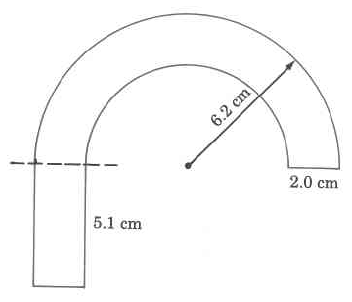
$A cane-shaped object of an even thickness, with one straight portion and one portion shaped in a half-circle. The thickness is 2.0cm, the length of the straight portion is 5.1cm, and the radius of the semicircle portion is 6.2cm.$

Solution

We notice that we have two semicircles (half circles).

The larger radius is 6.2 cm.

The smaller radius is $\text{6.2 cm - 2.0 cm = 4.2 cm.}$

The width of the bottom part of the rectangle is 2.0 cm.

$\begin{array} {rcll} {\text{Perimeter}} & = & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {\text{2.0 cm}} & {} \\ {} & & {\text{5.1 cm}} & {} \\ {} & & {(0.5) \cdot (2) \cdot (3.14) \cdot \text{(6.2 com)}} & {\text{Circumference of outer semicircle.}} \\ {} & \ \ + & {\underline{(0.5) \cdot (2) \cdot (3.14) \cdot \text{(4.2 com)}}} & {\text{Circumference of inner semicircle.}} \\ {} & & {} & {\text{6.2 cm - 2.0 cm = 4.2 cm}} \\ {} & & {} & {\text{The 0.5 appears because we want the}} \\ {} & & {} & {\text{perimeter of only half a circle.}} \end{array}$

$\begin{array} {rcr} {\text{Perimeter}} & \approx & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{2.0 cm}} \\ {} & & {\text{5.1 cm}} \\ {} & & {\text{19.468 cm}} \\ {} & & {\underline{\text{+13.188 cm}}} \\ {} & & {\text{48.856 cm}} \end{array}$

Practice Set B

Find the outside perimeter of

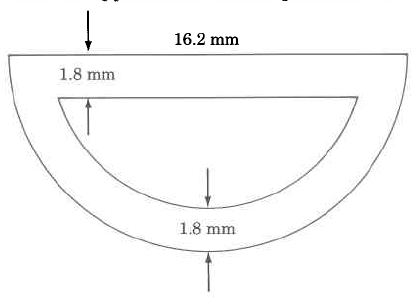
$A shape best visualized as a hollow half-circle. The thickness is 1.8mm, and the diameter of the widest portion of the half-circle is 16.2mm.$

Answer: 41.634 mm

Exercises

Find each perimeter or approximate circumference. Use $\pi = 3.14$.

Exercise $\PageIndex{1}$

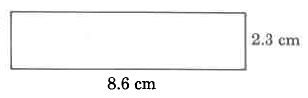
$A rectangle with sides of length 2.3cm and 8.6cm.$

Answer: 21.8 cm

Exercise $\PageIndex{2}$

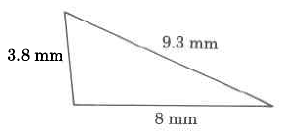
$A triangle with sides of length 8mm, 9.3mm, and 3.8mm.$

Exercise $\PageIndex{3}$

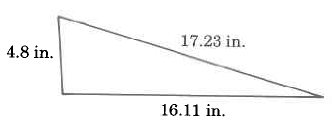
$A triangle with sides of length 4.8in, 16.11in, and 17.23in.$

Answer: 38.14 inches

Exercise $\PageIndex{4}$

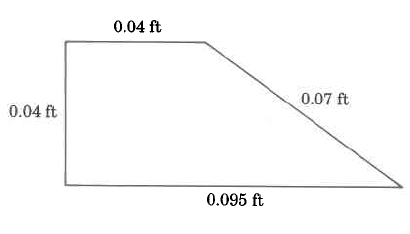
$A four-sided polygon with sides of length 0.04ft, 0.07ft, 0.04ft, and 0.095ft.$

Exercise $\PageIndex{5}$

$A four sided parallelogram with short sides of length 0.12m and long sides of length 0.31m.$

Answer: 0.86 m

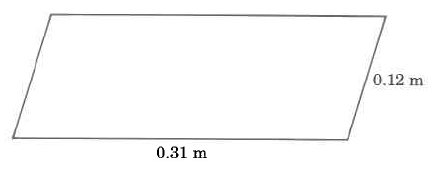
Exercise $\PageIndex{6}$

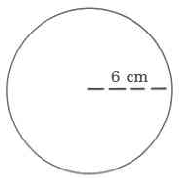
$A circle of radius 6m.$

Exercise $\PageIndex{10}$

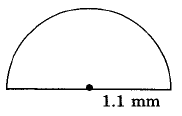
$A half-circle of diameter 1.1mm.$

Exercise $\PageIndex{12}$

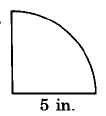
$A quarter-circle of radius 5 in.$

Exercise $\PageIndex{13}$

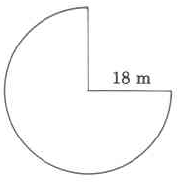
$Three quarters of a circle. The radius is 18m.$

Answer: 120.78 m

Exercise $\PageIndex{14}$

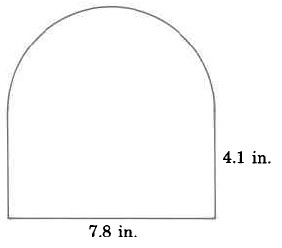
$A shape best visualized as a rectangle connected to a half-circle on top. The rectangle's height is 4.1in, and the rectangle's width is 7.8in.$

Exercise $\PageIndex{16}$

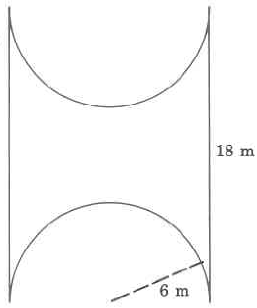
$A shape best described as a rectangle with two half-circle slices taken out of the top and bottom. The rectangle's height is 18m, and the radius of the circles is 6m.$

Exercise $\PageIndex{17}$

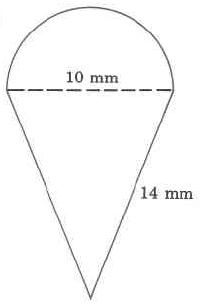
$A shape best described as an ice cream cone, or a triangle with a half-circle attached to the top. The sides of the triangle are measured to be 14mm, and the diameter of the half-circle is 10mm.$

Answer: 43.7 mm

The Meaning and Notation for Area

The product $\text{(length unit)} \cdot \text{(length unit)} = \text{(length unit)}^2$, or, square length unit (sq length unit), can be interpreted physically as the area of a surface.

Area
The area of a surface is the amount of square length units contained in the surface.

For example, 3 sq in. means that 3 squares, 1 inch on each side, can be placed precisely on some surface. (The squares may have to be cut and rearranged so they match the shape of the surface.)

We will examine the area of the following geometric figures.

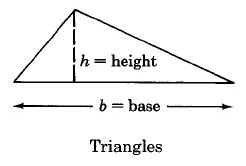
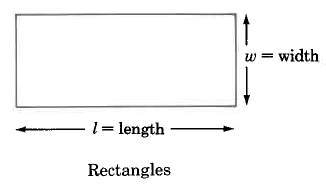
$Triangles, a three-sided polygon, have a height, h, measured from bottom to top, and base, b, measured from one end to the other of the bottom side.$ $Rectangles, a four-sided polygon, have a width, w, in this case the vertical side, and a length, l, in this case the horizontal side.$

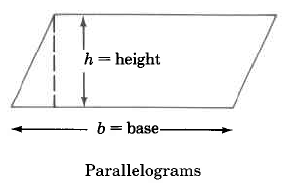
$Parallelograms, a four-sided polygon with diagonal sides in the same direction have a height, h, measured as the distance from the bottom to top, and a base, b, measured as the width of the horizontal side.$ $Trapezoids, a four-sided polygon with diagonal sides facing leaning into each other, have a height measured as the distance between the two bases. Trapezoids have two bases of differing lengths, base 1, and base 2.$

$Circles. The distance across the circle is the diameter. The distance from the center of the circle to the edge is the radius.$

Area Formulas

We can determine the areas of these geometric figures using the following formulas.

	Figure	Area Formula	Statement
$A triangle.$	Triangle	$A_T = \dfrac{1}{2} \cdot b \cdot h$	Area of a triangle is one half the base times the height.
$A rectangle.$	Rectangle	$A_R = l \cdot w$	Area of a rectangle is the length times the width.
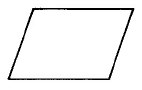$A parallelogram.$	Parallelogram	$A_P = b \cdot h$	Area of a parallelogram is base times the height.
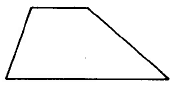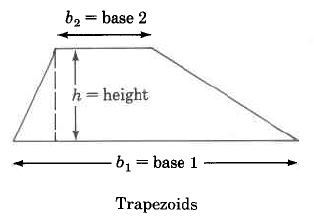
$A trapezoid.$	Trapezoid	$A_{Trap} = \dfrac{1}{2} \cdot (b_1 + b_2) \cdot h$	Area of a trapezoid is one half the sum of the two bases times the height.
$A circle.$	Circle	$A_c = \pi r^2$	Area of a circle is $\pi$ times the square of the radius.

Finding Areas of Some Common Geometric Figures

Sample Set A

Find the area of the triangle.

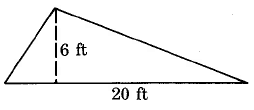
$A triangle with height 6 feet and length 20 feet.$

Solution

$\begin{array} {rcl} {A_T} & = & {\dfrac{1}{2} \cdot b \cdot h} \\ {} & = & {\dfrac{1}{2} \cdot 20 \cdot 5 \text{ sq ft}} \\ {} & = & {10 \cdot 6 \text{ sq ft}} \\ {} & = & {60 \text{ sq ft}} \\ {} & = & {60 \text{ ft}^2} \end{array}$

The area of this triangle is 60 sq ft, which is often written as 60 $\text{ft}^2$.

Sample Set A

Find the area of the rectangle.

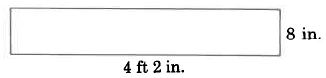
$A rectangle with width 4 feet 2 inches and height 8 inches.$

Solution

Let's first convert 4 ft 2 in. to inches. Since we wish to convert to inches, we'll use the unit fraction $\dfrac{\text{12 in.}}{\text{1 ft}}$ since it has inches in the numerator. Then,

$\begin{array} {rcl} {\text{4 ft}} & = & {\dfrac{\text{4 ft}}{1} \cdot \dfrac{\text{12 in.}}{\text{1 ft}}} \\ {} & = & {\dfrac{4 \cancel{\text{ ft}}}{1} \cdot \dfrac{\text{12 in.}}{1 \cancel{\text{ ft}}}} \\ {} & = & {\text{48 in.}} \end{array}$

Thus, $\text{4 ft 2 in. = 48 in. + 2 in. = 50 in.}$

$\begin{array} {rcl} {A_R} & = & {l \cdot w} \\ {} & = & {\text{50 in.} \cdot \text{8 in.}} \\ {} & = & {400 \text{ sq in.}} \end{array}$

The area of this rectangle is 400 sq in.

Sample Set A

Find the area of the parallelogram.

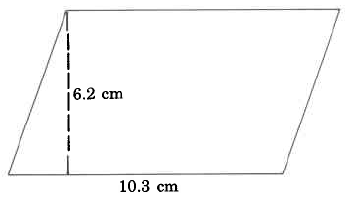
$A parallelogram with base 10.3cm and height 6.2cm$

Solution

$\begin{array} {rcl} {A_P} & = & {b \cdot h} \\ {} & = & {\text{10.3 cm} \cdot \text{6.2 cm}} \\ {} & = & {63.86 \text{ sq cm}} \end{array}$

The area of this parallelogram is 63.86 sq cm.

Sample Set A

Find the area of the trapezoid.

$A trapezoid with height 4.1mm, bottom base 20.4mm, and top base 14.5mm.$

Solution

$\begin{array} {rcl} {A_{Trap}} & = & {\dfrac{1}{2} \cdot (b_1 + b_2) \cdot h} \\ {} & = & {\dfrac{1}{2} \cdot (\text{14.5 mm + 20.4 mm}) \cdot (4.1 \text{ mm})} \\ {} & = & {\dfrac{1}{2} \cdot (\text{34.9 mm}) \cdot (4.1 \text{ mm})} \\ {} & = & {\dfrac{1}{2} \cdot \text{(143.09 sq mm)}} \\ {} & = & {71.545 \text{ sq mm}} \end{array}$

The area of this trapezoid is 71.545 sq mm.

Sample Set A

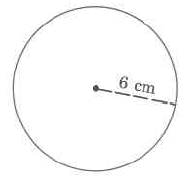
Find the approximate area of the circle.

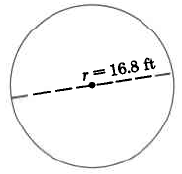
$A circle with radius 16.8ft.$

Solution

$\begin{array} {rcl} {A_c} & = & {\pi \cdot r^2} \\ {} & \approx & {(3.14) \cdot (16.8 \text{ ft})^2} \\ {} & \approx & {(3.14) \cdot (\text{282.24 sq ft})} \\ {} & \approx & {888.23 \text{ sq ft}} \end{array}$

The area of this circle is approximately 886.23 sq ft.

Practice Set A

Find the area of each of the following geometric figures.

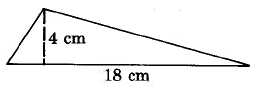
$A triangle with base 18cm and height 4cm.$

Answer: 36 sq cm

Practice Set A

$A rectangle with base 9.26mm and height 4.05mm.$

Answer: 37.503 sq mm

Practice Set A

$A parallelogram with base 5.1in and height 2.6in.$

Answer: 13.26 sq in.

Practice Set A

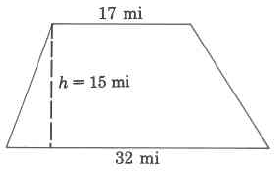
$A trapezoid with height 15mi, bottom base 32mi, and top base 17mi.$

Answer: 367.5 sq mi

Practice Set A

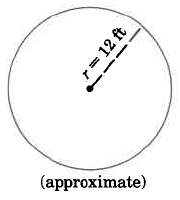
$A circle with radius r = 12ft.$

Answer: 452.16 sq ft

Practice Set A

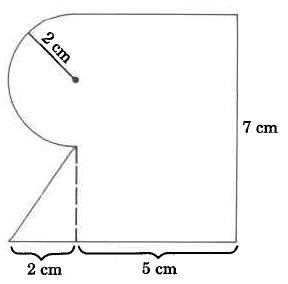
$A shape composed of a half circle of radius 2cm, a rectangle with base 5cm and height 7cm, and a triangle with base 2cm and height 3cm.$

Answer: 44.28 sq cm

The Meaning and Notation for Volume

The product $\text{(length unit)}\text{(length unit)}\text{(length unit)} = \text{(length unit)}^3$, or cubic length unit (cu length unit), can be interpreted physically as the volume of a three-dimensional object.

Volume
The volume of an object is the amount of cubic length units contained in the object.

For example, 4 cu mm means that 4 cubes, 1 mm on each side, would precisely fill some three-dimensional object. (The cubes may have to be cut and rearranged so they match the shape of the object.)

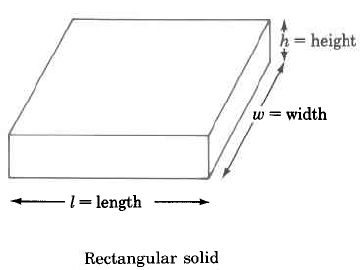
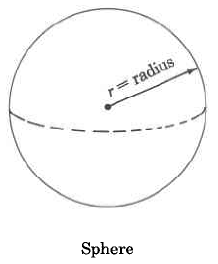
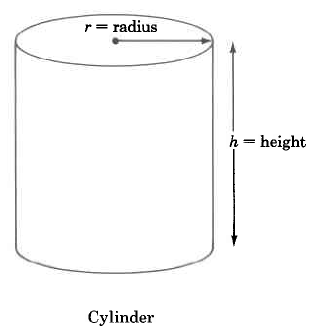
$A rectangular solid, with length l, width w, and height h.$ $A sphere with radius r.$ $A cylinder with height h and radius r.$ $A cone with height h and radius r.$

Volume Formulas

	Figure	Volume Formula	Statement
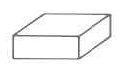$A rectangular solid.$	Rectangular solid	$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a rectangular solid is the length times the width times the height.
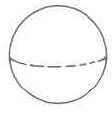$A sphere.$	Sphere	$V_s = \dfrac{4}{3} \cdot \pi \cdot r^3$	The volume of a sphere is $\dfrac{4}{3}$ times $\pi$ times the cube of the radius.
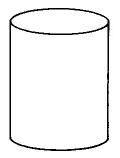$A cylinder.$	Cylinder	$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a cylinder is $\pi$ times the square of the radius times the height.
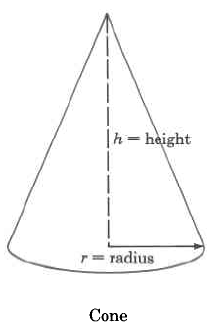
$A cone.$	Cone	$\begin{array} {rcl} {V_c} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\ {} & = & {\text{(area of base)} \cdot \text{(height)}} \end{array}$	The volume of a cone is $\dfrac{1}{3}$ times $\pi$ times the square of the radius times the height.

Finding Volumes of Some Common Geometric Objects

Sample Set B

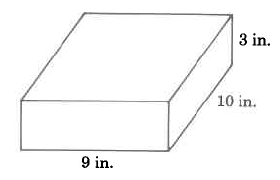
Find the volume of the rectangular solid.

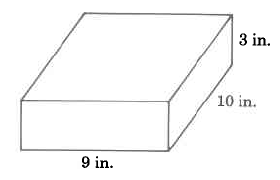
$A rectangular solid with width 9in, length 10in, and height 3in.$

Solution

$\begin{array} {rcl} {V_R} & = & {l \cdot w \cdot h} \\ {} & = & {\text{9 in.} \cdot \text{10 in.} \cdot \text{3 in.}} \\ {} & = & {\text{270 cu in.}} \\ {} & = & {\text{270 in.}^3} \end{array}$

The volume of this rectangular solid is 270 cu in.

Sample Set B

Find the approximate volume of the sphere.

$A circle with radius 6cm.$

Solution

$\begin{array} {rcl} {V_S} & = & {\dfrac{4}{3} \cdot \pi \cdot r^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(6 cm)}^3} \\ {} & \approx & {(\dfrac{4}{3}) \cdot (3.14) \cdot \text{(216 cu cm)}} \\ {} & \approx & {\text{904.32 cu cm}} \end{array}$

The approximate volume of this sphere is 904.32 cu cm, which is often written as 904.32 cm$^3$.

Sample Set B

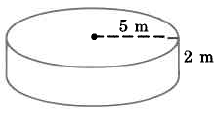
Find the approximate volume of the cylinder.

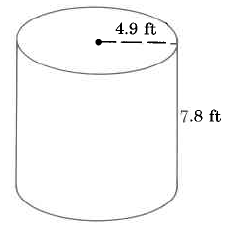
$A cylinder with radius 4.9ft and height 7.8ft.$

Solution

$\begin{array} {rcl} {V_{Cyl}} & = & {\pi \cdot r^2 \cdot h} \\ {} & \approx & {(3.14) \cdot (\text{4.9 ft})^2 \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot (\text{24.01 sq ft}) \cdot \text{(7.8 ft)}} \\ {} & \approx & {(3.14) \cdot \text{(187.278 cu ft)}} \\ {} & \approx & {\text{588.05292 cu ft}} \end{array}$

The volume of this cylinder is approximately 588.05292 cu ft. The volume is approximate because we approximated $\pi$ with 3.14.

Sample Set B

Find the approximate volume of the cone. Round to two decimal places.

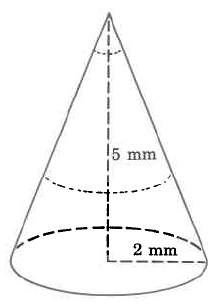
$A cone with height 5mm and radius 2mm$

Solution

$\begin{array} {rcl} {V_{c}} & = & {\dfrac{1}{3} \cdot \pi \cdot r^2 \cdot h} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{2 mm})^2 \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot (\text{4 sq mm}) \cdot \text{(5 mm)}} \\ {} & \approx & {(\dfrac{1}{3}) \cdot (3.14) \cdot \text{(20 cu mm)}} \\ {} & \approx & {20.9\overline{3} \text{ cu mm}} \\ {} & \approx & {\text{20.93 cu mm}} \end{array}$

The volume of this cone is approximately 20.93 cu mm. The volume is approximate because we approximated $\pi$ with 3.14.

Practice Set B

Find the volume of each geometric object. If $\pi$ is required, approximate it with 3.14 and find the approximate volume.

$A rectangular solid with width 9in, length 10in, and height 3in.$

Answer: 21 cu in.

Practice Set B

Sphere

$A sphere with radius 6cm.$

Answer: 904.32 cu ft

Practice Set B

$A cylinder with radius 5m and height 2m.$

Answer: 157 cu m

Practice Set B

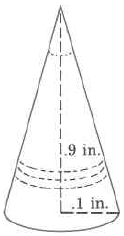
$A cone with height .9in and radius .1 in.$

Answer: 0.00942 cu in.

Exercises

Find each indicated measurement.

Exercise $\PageIndex{1}$

Area

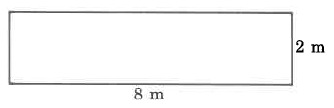
$A rectangle with width 8m and height 2m$

Answer: 16 sq m

Exercise $\PageIndex{2}$

Area

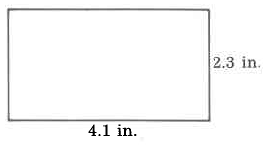
$A rectangle with width 4.1in and height 2.3in.$

Exercise $\PageIndex{3}$

Area

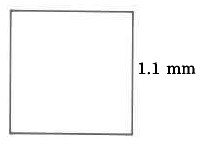
Answer: 1.21 sq mm

Exercise $\PageIndex{4}$

Area

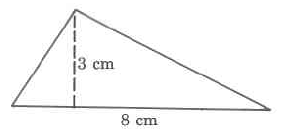
$A triangle with base 8cm and height 3cm.$

Exercise $\PageIndex{5}$

Area

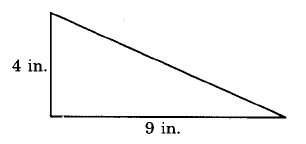
$A triangle with base 9in and height 4in.$

Answer: 18 sq in.

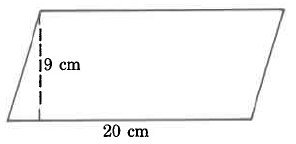
Exercise $\PageIndex{6}$

Area

$A parallelogram with base 20cm and height 9cm.$

Exercise $\PageIndex{7}$

Exact area

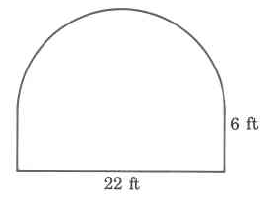
$A rectangle with a half-circle on top. The rectangle's width is 22ft, which is also the diameter of the circle, and the rectangle's height is 6ft.$

Answer: $(60.5 \pi + 132) \text{ sq ft}$

Exercise $\PageIndex{8}$

Approximate area

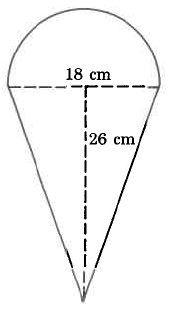
$A triangle with a half-circle on top, like an ice cream cone. The circle's diameter is 18cm, and the height of the triangle is 26cm.$

Exercise $\PageIndex{9}$

Area

Answer: 40.8 sq in.

Exercise $\PageIndex{10}$

Area

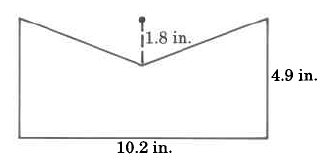
$A trapezoid with bottom base 15 mm, top base 7 mm, and height 8 mm.$

Exercise $\PageIndex{11}$

Approximate area

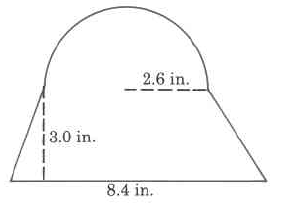
$A shape composed of a trapezoid with a half-circle on top. The circle's diameter is the width of the top base. The bottom base is 8.4in, the height of the trapezoid portion is 3.0in, and the radius of the circle is 2.6in.$

Answer: 31.0132 sq in.

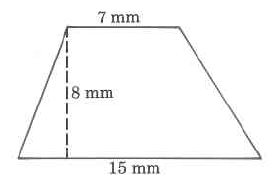
Exercise $\PageIndex{12}$

Exact area

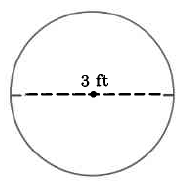
$A circle with a diameter of 3ft.$

Exercise $\PageIndex{13}$

Approximate area

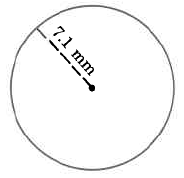
$A circle with a radius of 7.1mm.$

Answer: 158.2874 sq mm

Exercise $\PageIndex{14}$

Exact area

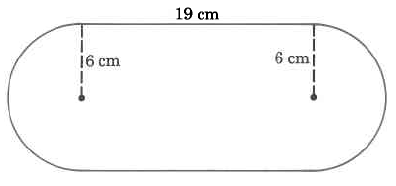
$A shape that looks like an ice rink. A rectangle with a half-circle attached to each end. The radius of the half-circles is 6cm, and the length of the rectangle is 19cm.$

Exercise $\PageIndex{15}$

Approximate area

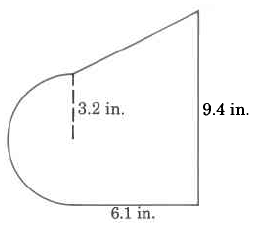
$A trapezoid with a half-circle attached to one base. The half-circle's radius is 3.2in. The other base is 9.4in. The height of the trapezoid is 6.1in.$

Answer: 64.2668 sq in.

Exercise $\PageIndex{16}$

Area

$A rectangle with a rectangle cut out of the inside. The inside rectangle has a width of 4.83in and a height of 1.61in. The outside rectangle has a width of 5.21in and a height of 1.74in.$

Exercise $\PageIndex{17}$

Approximate area

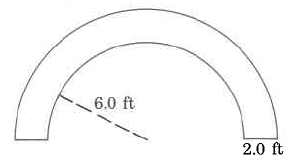
$A tubelike shape in a half circle. The inner circle's radius is 6.0ft. The tube's thickness is 2.0ft.$

Answer: 43.96 sq ft

Exercise $\PageIndex{18}$

Volume

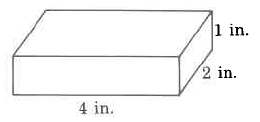
$A rectangular solid with width 4in, length 2in, and height 1in.$

Exercise $\PageIndex{19}$

Volume

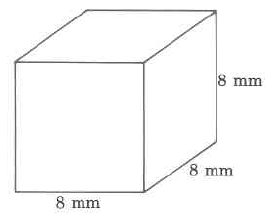
$A rectangular solid with width 8mm, length 8mm, and height 8mm.$

Answer: 512 cu cm

Exercise $\PageIndex{20}$

Exact volume

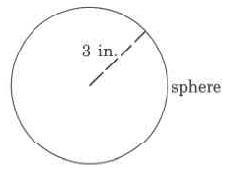
$A sphere with a radius of 3in.$

Exercise $\PageIndex{21}$

Approximate volume

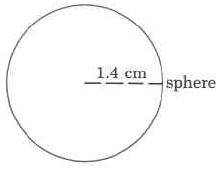
$A sphere with a radius of 1.4cm.$

Answer: 11.49 cu cm

Exercise $\PageIndex{22}$

Approximate volume

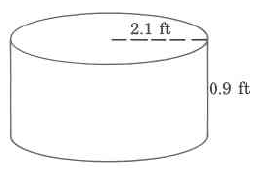
$A cylinder with a radius of 2.1ft and a height of 0.9ft.$

Exercise $\PageIndex{23}$

Exact volume

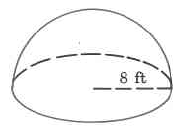
$Half of a sphere with radius 8ft.$

Answer: $\dfrac{1024}{3} \pi \text{ cu ft}$

Exercise $\PageIndex{24}$

Approximate volume

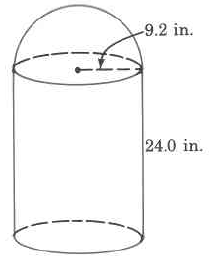
$A cylinder with a half-sphere on top. The object's radius is 9.2in, and the height of the cylinder is 24.0in.$

Exercise $\PageIndex{25}$

Approximate volume

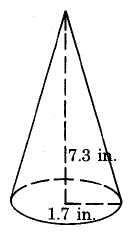
$A cone with radius 1.7in and height 7.3in.$

Answer: 22.08 cu in.

Exercise $\PageIndex{26}$

Approximate volume

$A cylinder with a cone on top. The object has a diameter of 3.0ft. The cone has a height of 3.0ft. The cylinder's height is 8.1ft.$

Exercises for Review

Exercise $\PageIndex{27}$

In the number 23,426, how many hundreds are there?

Answer: 4

Exercise $\PageIndex{28}$

List all the factors of 32.

Exercise $\PageIndex{29}$

Find the value of $4 \dfrac{3}{4} - 3 \dfrac{5}{6} + 1 \dfrac{2}{3}$.

Answer: $\dfrac{31}{12} = 2 \dfrac{7}{12} = 2.58$

Exercise $\PageIndex{30}$

Find the value of $\dfrac{5 + \dfrac{1}{3}}{2 + \dfrac{2}{15}}$.

Exercise $\PageIndex{31}$

Find the perimeter.

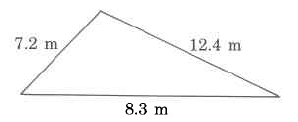
$A triangle with sides of the following lengths: 7.2m, 8.3m, and 12.4m.$

Answer: 27.9m

Area (A) is measured in square units, perimeter (P) is measured in units, and circumference (C) is measured in units.

Square

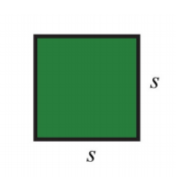Screenshot (282).png — Figure $\PageIndex{1}$

\[P=4 s \]

\[A=s^{2}\]

Rectangle

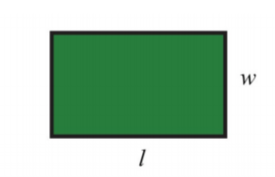Screenshot (283).png — Figure $\PageIndex{2}$

\[P=2 l+2 w \]

\[A=l w\]

Parallelogram

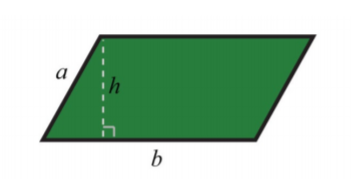Screenshot (284).png — Figure $\PageIndex{3}$

\[P=2 a+2 b\]

\[A=b h\]

Trapezoid

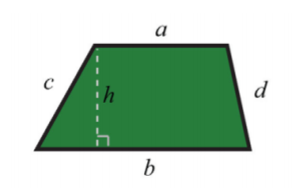Screenshot (285).png — Figure $\PageIndex{4}$

\[P=a+b+c+d\]

\[A=\frac{1}{2} h(a+b)\]

Triangle

Screenshot (286).png — Figure $\PageIndex{5}$

\[P=a+b+c\]

\[A=\frac{1}{2} b h\]

Circle

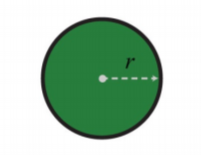Screenshot (287).png — Figure $\PageIndex{6}$

\[C=2 \pi \]

\[r=\pi r^{2}\]

Volume (V) is measured in cubic units and surface area (SA) is measured in square units.

Cube

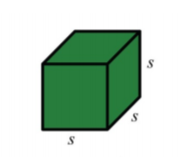Screenshot (288).png — Figure $\PageIndex{1}$

\[S A=6 s^{2}\]

\[V=s^{3}\]

Rectangular Solid

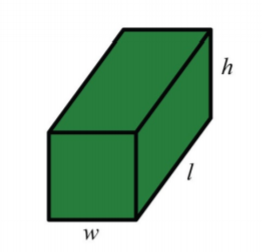Screenshot (289).png — Figure $\PageIndex{2}$

\[S A=2 l w+2 l h+2 w h\]

\[V=l w h\]

Right Circular Cylinder

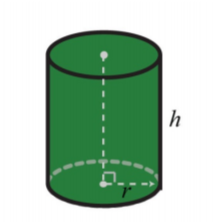Screenshot (290).png — Figure $\PageIndex{3}$

\[S A=2 \pi r^{2}+2 \pi r h\]

\[V=\pi r^{2} h\]

Right Circular Cone

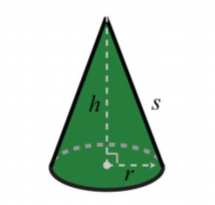Screenshot (292).png — Figure $\PageIndex{4}$

\[S A=\pi r^{2}+\pi r s\]

\[V=\frac{1}{3} \pi r^{2} h\]

Sphere

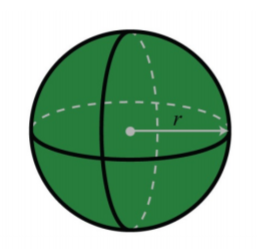Screenshot (293).png — Figure $\PageIndex{5}$

\[S A=4 \pi r^{2}\]

\[V=\frac{4}{3} \pi r^{3}\]

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Polygon

Definition: Perimeter

Sample Set A

Sample Set A

Sample Set A

Sample Set B

Sample Set B

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set A

Sample Set B

Sample Set B

Sample Set B

Sample Set B