9.8: The Eye
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Understand the basic physics of how images are formed by the human eye
- Recognize several conditions of impaired vision as well as the optics principles for treating these conditions
Physics of the Eye
The eye is remarkable in how it forms images and in the richness of detail and color it can detect. However, our eyes often need some correction to reach what is called “normal” vision. Actually, normal vision should be called “ideal” vision because nearly one-half of the human population requires some sort of eyesight correction, so requiring glasses is by no means “abnormal.” Image formation by our eyes and common vision correction can be analyzed with the optics discussed earlier in this chapter.
Figure 9.8.1 shows the basic anatomy of the eye. The cornea and lens form a system that, to a good approximation, acts as a single thin lens. For clear vision, a real image must be projected onto the light-sensitive retina, which lies a fixed distance from the lens. The flexible lens of the eye allows it to adjust the radius of curvature of the lens to produce an image on the retina for objects at different distances. The center of the image falls on the fovea, which has the greatest density of light receptors and the greatest acuity (sharpness) in the visual field. The variable opening (i.e., the pupil) of the eye, along with chemical adaptation, allows the eye to detect light intensities from the lowest observable to 1010times greater (without damage). This is an incredible range of detection. Processing of visual nerve impulses begins with interconnections in the retina and continues in the brain. The optic nerve conveys the signals received by the eye to the brain.
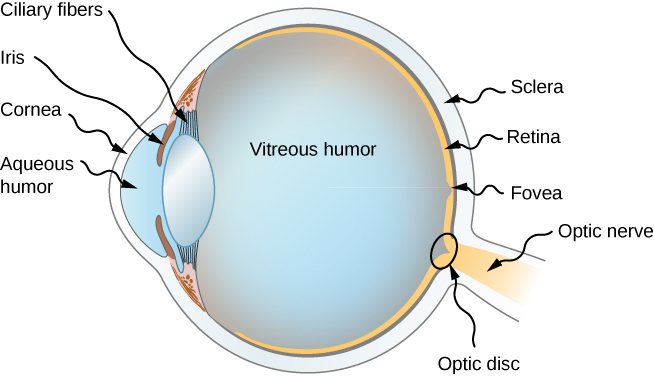
The indices of refraction in the eye are crucial to its ability to form images. Table 9.8.1 lists the indices of refraction relevant to the eye. The biggest change in the index of refraction, which is where the light rays are most bent, occurs at the air-cornea interface rather than at the aqueous humor-lens interface. The ray diagram in Figure 9.8.2 shows image formation by the cornea and lens of the eye. The cornea, which is itself a converging lens with a focal length of approximately 2.3 cm, provides most of the focusing power of the eye. The lens, which is a converging lens with a focal length of about 6.4 cm, provides the finer focus needed to produce a clear image on the retina. The cornea and lens can be treated as a single thin lens, even though the light rays pass through several layers of material (such as cornea, aqueous humor, several layers in the lens, and vitreous humor), changing direction at each interface. The image formed is much like the one produced by a single convex lens (i.e., a real, inverted image). Although images formed in the eye are inverted, the brain inverts them once more to make them seem upright.
| Material | Index of Refraction |
|---|---|
| Water | 1.33 |
| Air | 1.0 |
| Cornea | 1.38 |
| Aqueous humor | 1.34 |
| Lens | 1.41* |
| Vitreous humor | 1.34 |
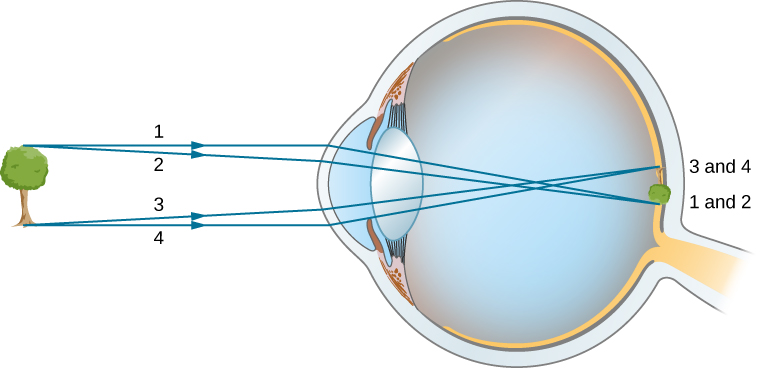
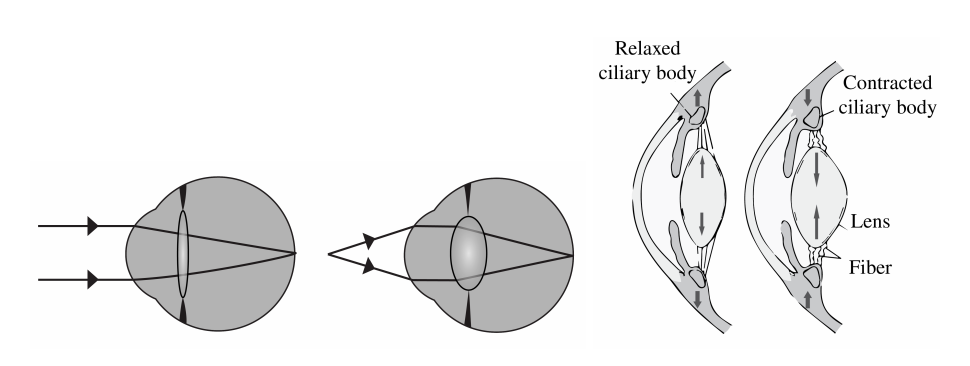
As noted, the image must fall precisely on the retina to produce clear vision—that is, the image distance di must equal the lens-to-retina distance. Because the lens-to-retina distance does not change, the image distance di must be the same for objects at all distances. The ciliary muscles adjust the shape of the eye lens for focusing on nearby or far objects. By changing the shape of the eye lens, the eye changes the focal length of the lens. This mechanism of the eye is called accommodation.
Figure 3 shows the accommodation of the eye for distant and near vision. Since light rays from a nearby object can diverge and still enter the eye, the lens must be more converging (more powerful) for close vision than for distant vision. To be more converging, the lens is made thicker by the action of the ciliary muscle surrounding it. The eye is most relaxed when viewing distant objects, one reason that microscopes and telescopes are designed to produce distant images. Vision of very distant objects is called totally relaxed, while close vision is termed accommodated, with the closest vision being fully accommodated.
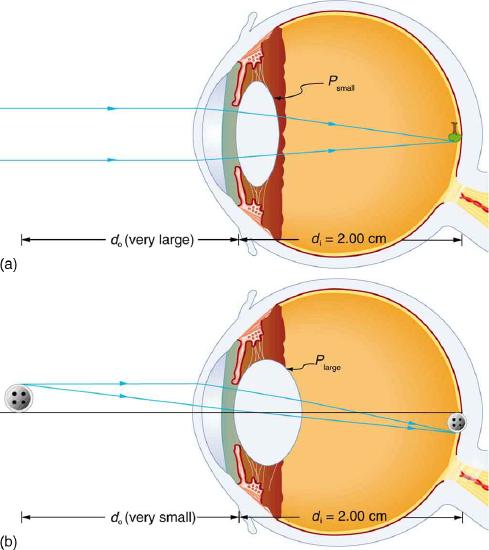
We will use the thin lens equations to examine image formation by the eye quantitatively. First, note the power of a lens is given as p=1/f, so we rewrite the thin lens equations as P=1do+1di
Look at the central transparent area of someone’s eye, the pupil, in normal room light. Estimate the diameter of the pupil. Now turn off the lights and darken the room. After a few minutes turn on the lights and promptly estimate the diameter of the pupil. What happens to the pupil as the eye adjusts to the room light? Explain your observations.
The eye can detect an impressive amount of detail, considering how small the image is on the retina. To get some idea of how small the image can be, consider the following example.
What is the size of the image on the retina of a 1.20×10−2 cm diameter human hair, held at arm’s length (60.0 cm) away? Take the lens-to-retina distance to be 2.00 cm.
Strategy:
We want to find the height of the image hi, given the height of the object is ho=1.20×10−2 cm. We also know that the object is 60.0 cm away, so that do=60.0cm. For clear vision, the image distance must equal the lens-to-retina distance, and so di=2.00cm. The equation hiho=−dido=m can be used to find hi with the known information.
Solution
The only unknown variable in the equation hiho=−dido=m is hi: hiho=−dido.
Discussion:
This truly small image is not the smallest discernible -- that is, the limit to visual acuity is even smaller than this. Limitations on visual acuity have to do with the wave properties of light and will be discussed in the next chapter. Some limitation is also due to the inherent anatomy of the eye and processing that occurs in our brain.
Calculate the power of the eye when viewing objects at the greatest and smallest distances possible with normal vision, assuming a lens-to-retina distance of 2.00 cm (a typical value).
Strategy:
For clear vision, the image must be on the retina, and so di=2.00cm here. For distant vision, do≈∞, and for close vision, do=25.0cm, as discussed earlier. The equation P=1do+1di as written just above, can be used directly to solve for P in both cases, since we know di and do. Power has units of diopters, where 1D=1/m, and so we should express all distances in meters.
Solution
For distant vision, P=1do+1di=1∞+10.0200m.
Discussion:
For an eye with this typical 2.00 cm lens-to-retina distance, the power of the eye ranges from 50.0 D (for distant totally relaxed vision) to 54.0 D (for close fully accommodated vision), which is an 8% increase. This increase in power for close vision is consistent with the preceding discussion and the ray tracing in Figure 3. An 8% ability to accommodate is considered normal but is typical for people who are about 40 years old. Younger people have greater accommodation ability, whereas older people gradually lose the ability to accommodate. When an optometrist identifies accommodation as a problem in elder people, it is most likely due to stiffening of the lens. The lens of the eye changes with age in ways that tend to preserve the ability to see distant objects clearly but do not allow the eye to accommodate for close vision, a condition called presbyopia (literally, elder eye). To correct this vision defect, we place a converging, positive power lens in front of the eye, such as found in reading glasses. Commonly available reading glasses are rated by their power in diopters, typically ranging from 1.0 to 3.5 D.
The nearest point an object can be placed so that the eye can form a clear image on the retina is called the near point of the eye. Similarly, the far point is the farthest distance at which an object is clearly visible. A person with normal vision can see objects clearly at distances ranging from 25 cm to essentially infinity. The near point increases with age, becoming several meters for some older people. In this text, we consider the near point to be 25 cm.
We can use the thin-lens equations to quantitatively examine image formation by the eye. First, we define the optical power of a lens as
P=1f
with the focal length f given in meters. The units of optical power are called “diopters” (D). That is, 1D=1/m,or 1m−1. Optometrists prescribe common eyeglasses and contact lenses in units of diopters. With this definition of optical power, we can rewrite the thin-lens equations as
P=1do+1di.
Working with optical power is convenient because, for two or more lenses close together, the effective optical power of the lens system is approximately the sum of the optical power of the individual lenses:
Ptotal=Plens 1+Plens 2+Plens 3+⋯
The cornea and eye lens have focal lengths of 2.3 and 6.4 cm, respectively. Find the net focal length and optical power of the eye.
Strategy
The optical powers of the closely spaced lenses add, so Peye=Pcornea+Plens.
Solution
Writing the equation for power in terms of the focal lengths gives
1feye=1fcornea+1flens=12.3cm+16.4cm.
Hence, the focal length of the eye (cornea and lens together) is
feye=1.69cm.
The optical power of the eye is
Peye=1feye=10.0169m=59D.
For clear vision, the image distance di must equal the lens-to-retina distance. Normal vision is possible for objects at distances do=25cm to infinity. The following example shows how to calculate the image distance for an object placed at the near point of the eye.
The net focal length of a particular human eye is 1.7 cm. An object is placed at the near point of the eye. How far behind the lens is a focused image formed?
Strategy
The near point is 25 cm from the eye, so the object distance is do=25 cm. We determine the image distance from the lens equation:
1di=1f−1do.
Solution
di=(1f−1do)−1
=(11.7cm−125cm)−1
=1.8cm
Therefore, the image is formed 1.8 cm behind the lens.
Significance
From the magnification formula, we find m=−1.8cm25cm=−0.073. Since m<0, the image is inverted in orientation with respect to the object. From the absolute value of m we see that the image is much smaller than the object; in fact, it is only 7% of the size of the object.
Vision Correction
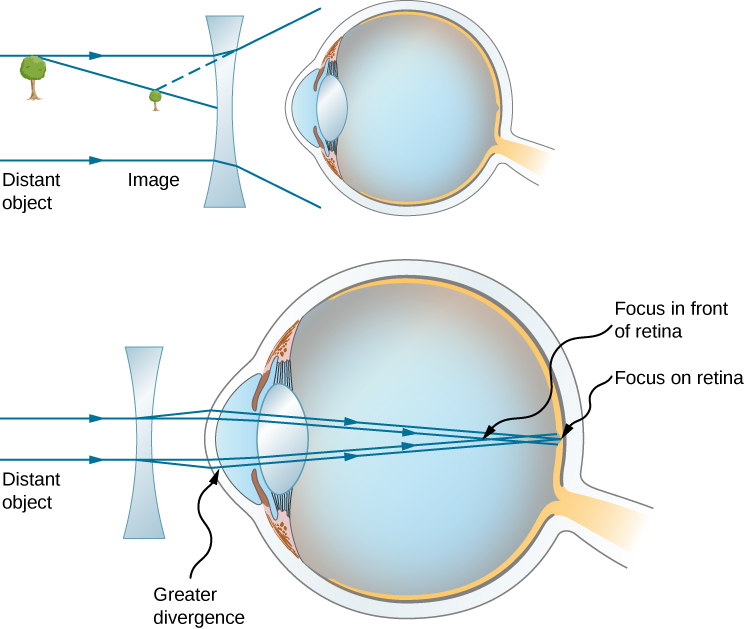
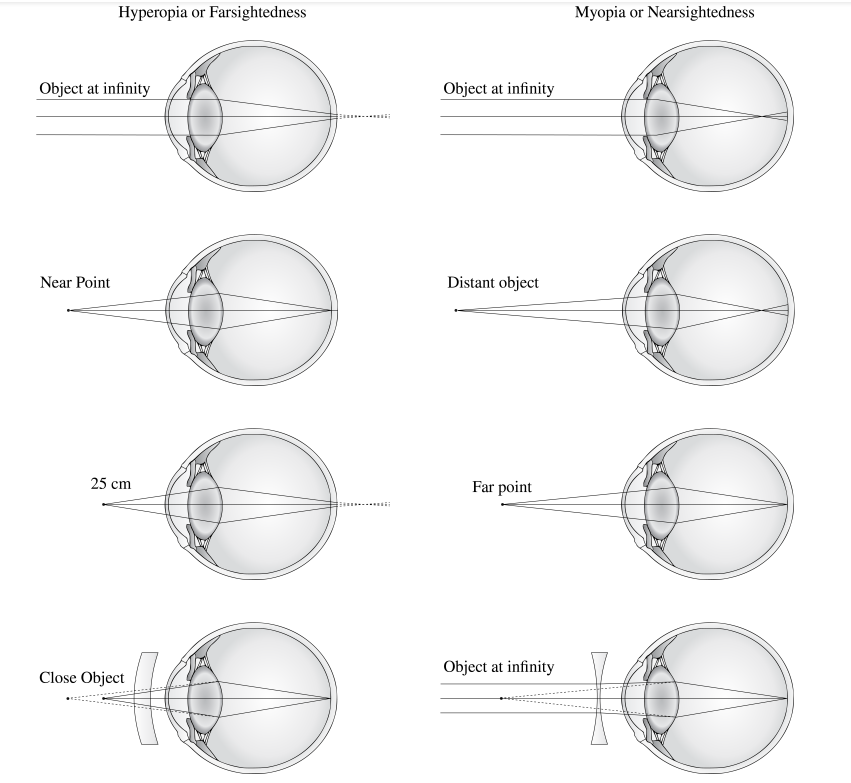
The need for some type of vision correction is very common. Typical vision defects are easy to understand with geometric optics, and some are simple to correct. Figure 9.8.3 illustrates two common vision defects. Nearsightedness, or myopia, is the ability to see near objects, whereas distant objects are blurry. The eye over converges the nearly parallel rays from a distant object, and the rays cross in front of the retina. More divergent rays from a close object are converged on the retina for a clear image. The distance to the farthest object that can be seen clearly is called the far point of the eye (normally the far point is at infinity). Farsightedness, or hyperopia, is the ability to see far objects clearly, whereas near objects are blurry. A farsighted eye does not sufficiently converge the rays from a near object to make the rays meet on the retina.
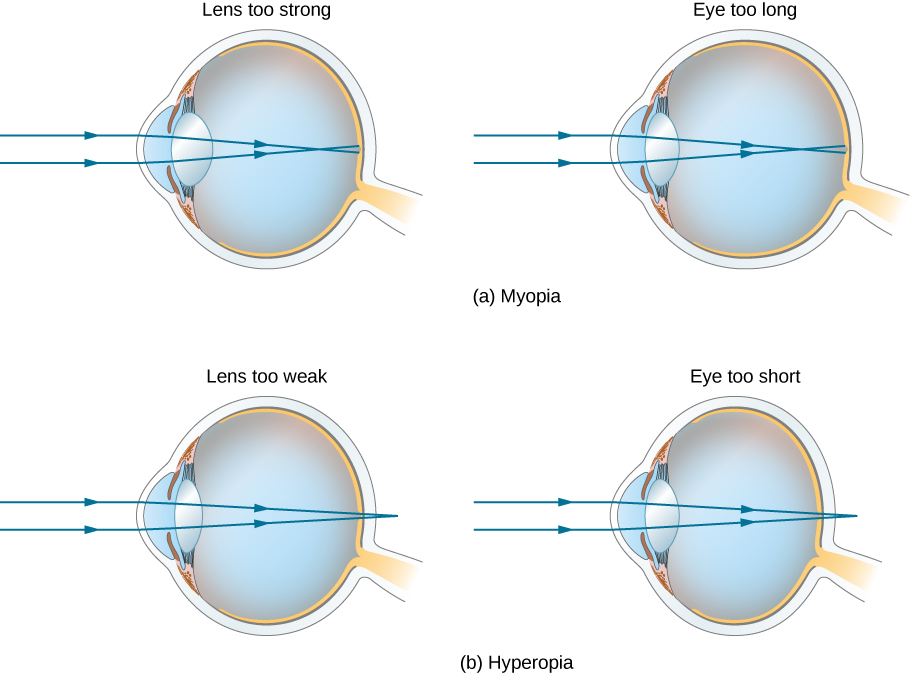
Since the nearsighted eye over converges light rays, the correction for nearsightedness consists of placing a diverging eyeglass lens in front of the eye, as shown in Figure 9.8.4. This reduces the optical power of an eye that is too powerful (recall that the focal length of a diverging lens is negative, so its optical power is negative). Another way to understand this correction is that a diverging lens will cause the incoming rays to diverge more to compensate for the excessive convergence caused by the lens system of the eye. The image produced by the diverging eyeglass lens serves as the (optical) object for the eye, and because the eye cannot focus on objects beyond its far point, the diverging lens must form an image of distant (physical) objects at a point that is closer than the far point.
What optical power of eyeglass lens is needed to correct the vision of a nearsighted person whose far point is 30.0 cm? Assume the corrective lens is fixed 1.50 cm away from the eye.
Strategy
You want this nearsighted person to be able to see distant objects clearly, which means that the eyeglass lens must produce an image 30.0 cm from the eye for an object at infinity. An image 30.0 cm from the eye will be 30.0 cm−1.50 cm=28.5 cm from the eyeglass lens. Therefore, we must have di=−28.5cm when do=∞. The image distance is negative because it is on the same side of the eyeglass lens as the object.
Solution
Since di and dodo are known, we can find the optical power of the eyeglass lens by using Equation ???:
P=1do+1di=1∞+1−0.285m=−3.51D.
Significance
The negative optical power indicates a diverging (or concave) lens, as expected. If you examine eyeglasses for nearsighted people, you will find the lenses are thinnest in the center. Additionally, if you examine a prescription for eyeglasses for nearsighted people, you will find that the prescribed optical power is negative and given in units of diopters.
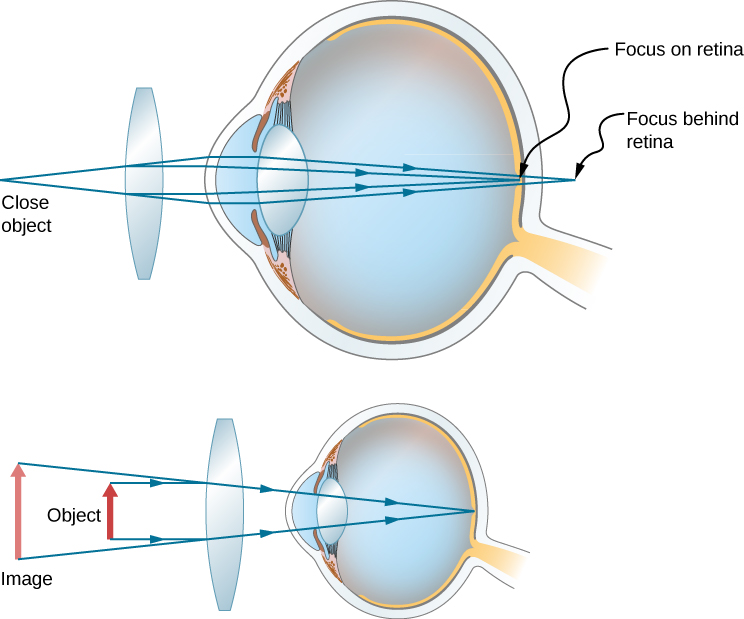
Correcting farsightedness consists simply of using the opposite type of lens as for nearsightedness (i.e., a converging lens), as shown in Figure 9.8.5.
Such a lens will produce an image of physical objects that are closer than the near point at a distance that is between the near point and the far point, so that the person can see the image clearly. To determine the optical power needed for correction, you must therefore know the person’s near point, as explained in Example 9.8.4.
What optical power of eyeglass lens is needed to allow a farsighted person, whose near point is 1.00 m, to see an object clearly that is 25.0 cm from the eye? Assume the corrective lens is fixed 1.5 cm from the eye.
Strategy
When an object is 25.0 cm from the person’s eyes, the eyeglass lens must produce an image 1.00 m away (the near point), so that the person can see it clearly. An image 1.00 m from the eye will be 100cm−1.5cm=98.5cm from the eyeglass lens because the eyeglass lens is 1.5 cm from the eye. Therefore, di=−98.5cm, where the minus sign indicates that the image is on the same side of the lens as the object. The object is 25.0cm−1.5cm=23.5cm from the eyeglass lens, so do=23.5cm.
Solution
Since di and dodo are known, we can find the optical power of the eyeglass lens by using Equation ???:
P=1do+1di=10.285m+1−0.985m=+3.24D.
Significance
The positive optical power indicates a converging (convex) lens, as expected. If you examine eyeglasses of farsighted people, you will find the lenses to be thickest in the center. In addition, prescription eyeglasses for farsighted people have a prescribed optical power that is positive.
Anatomy of the Eye
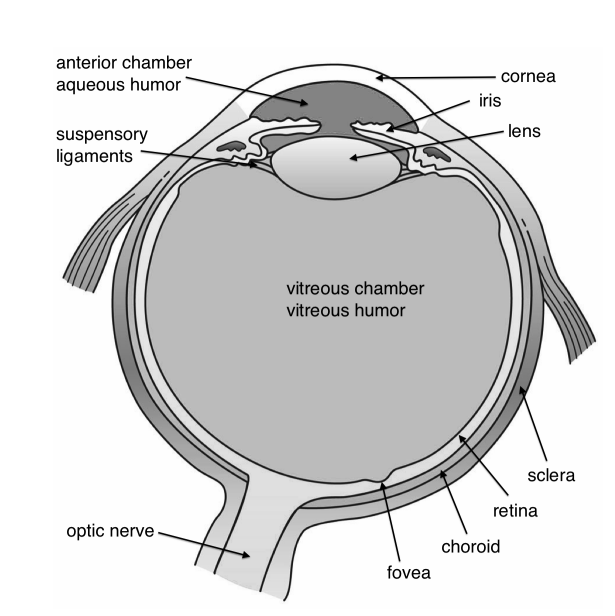
Our sense of vision occurs due to transduction of light stimuli received through the eyes. The eyes are located within either orbit in the skull. See Figure 9.8.1[1] for an illustration of the eye. The eyelids, with lashes at their leading edges, help to protect the eye from abrasions by blocking particles that may land on the surface of the eye. The inner surface of each lid is a thin membrane known as the conjunctiva. The conjunctiva extends over the white areas of the eye called the sclera, connecting the eyelids to the eyeball. The iris is the colored part of the eye. The iris is a smooth muscle that opens and closes the pupil, the hole at the center of the eye that allows light to enter. The iris constricts the pupil in response to bright light and dilates the pupil in response to dim light. The cornea is the transparent front part of the eye that covers the iris, pupil, and anterior chamber. The cornea, with the anterior chamber and lens, refracts light and contributes to vision. The cornea can be reshaped by surgical procedures such as LASIK. The innermost layer of the eye is the retina that contains the nervous tissue and specialized cells called photoreceptors for the initial processing of visual stimuli. Two types of photoreceptors within the retina are the rods and the cones. The cones are sensitive to different wavelengths of light and provide color vision. These nerve cells of the retina leave the eye and enter the brain via the optic nerve (cranial nerve II).[2]

Tears are produced by the lacrimal gland that is located beneath the lateral edges of the nose. Tears flow through the lacrimal duct to the medial corner of the eye and flow over the conjunctiva to wash away foreign particles. Movement of the eye within the orbit occurs by the contraction of six extraocular muscles that originate from the bones of the orbit and insert into the surface of the eyeball. The extraocular muscles are innervated by the abducens nerve, the trochlear nerve, and the oculomotor nerve (cranial nerves III, IV, and V).[3] See the illustration of the extraocular muscles in Figure 9.8.2.[4]

More Anatomy
The human eye is made of an almost spherical (24 mm long and 22 mm across) gelatinous substance called the vitreous humor with refractive index 1.337, surrounded by a white shell, the sclera (Figure 9.8.3). At the front, the sclera has an opening with a transparent lens called the cornea, with for green light an index of refraction of 1.376. Most of the bending of the rays takes place at the air-cornea interface and this is why it is difficult to see under water (nwater = 1.33). After passing the cornea, the rays reach the aqueous humour (n ≈1.336) with the iris (i.e. pupil). It can expand or contract from a 2 mm (bright sun) to 8 mm (low light) diameter to adapt to the light intensity. The iris gives colour to the eye. After the iris, the rays reach the flexible crystalline lens which has the size of a bean (9 mm in diameter, and 4 mm thick in unaccommodated condition). Its index of refraction varies from 1.406 in the centre to 1.386 at the edge.
Working of the eye
The entire eye can very accurately be treated as two lenses in contact, of which the crystalline lens can change its focal length. Often the system is approximated by only a single lens. In unaccommodated condition, the first focal distance of the lens system is fo = 16 mm as measured from the cornea. The second focal distance is equal to the length of the eye: fi = 24 mm. These focal distances are different, because the refractive indices of the surrounding medium (air and vitreous humour) differ. The power of the intact, unaccommodated eye lens system is, according to (2.5.35), (2.5.39):
D=nvhf2=1.3370.0243=55 Diopter.
In relaxed condition the lens focuses light coming from infinity on the retina. When the object is closer, the eye muscles contract due to which the crystalline lens becomes more convex and the focal length of the system decreases, as seen on the right of Figure 9.8.4. At a certain point, the object will be too close to be focused on the retina. This is called the near point of the eye. Due to the loss of elasticity of the muscle, the near point moves from 7 cm for teens to 100 cm for a 60-year-old. Figure 9.8.4 shows the optical rays entering the eyes, for two configurations: an object at infinity and an object nearby. The so-called normal near point is at 25 cm. The far point is the furthest object which is imaged on the retina by the unaccommodated eye. For the normal eye the far point is at infinity.
Retina
The retina is composed of approximately 125 million photoreceptor cells: the rods and the cones. The rods are highly sensitive black and white (intensity) sensors, while the cones are colour sensitive for the wavelengths 390 nm - 780 nm. UV light is absorbed by the lens (people whose lens is removed because of cataract can "see" UV light). The fovea centralis is the most sensitive centre of the retina with a high density of cones. The eyes move continuously to focus the image on this area. The information is transferred by the optical nerve, placed at the back of the eye, where it causes a blind spot.
Dioptric Power of a lens
For a combination of two thin lenses, it is not so easy to derive the resulting focal length from the individual focal length of the lenses. It is easier to consider the dioptric power. For a single lens the dioptric power is defined by:
D=1f=(ni−1)(1R1−1R2)
with R1 and R2 the radii of the thin lens and ni the index of refraction of the glass. Because for two lenses in contact, the focal length is given by:
1f=1f1+1f2,
the combined power of the two lenses is the sum of the individual powers:
D=D1+D2
A lens of focal length f1=10 cm has a dioptric power D1=10D. If it is in contact with a negative lens of dioptric power D2=−10D, the resulting power is D=0, equivalent to a parallel sheet of glass.
Common Disorders of the Eye
Eye disorders that nurses commonly see in practice include myopia, presbyopia, color blindness, dry eye, conjunctivitis, styes, cataracts, macular degeneration, and glaucoma.
Myopia
Myopia or Nearsightedness is impaired vision that makes far-away objects look blurry. It happens when the eyeball grows too long from front to back or when there are problems with the shape of the cornea or the lens. These problems make light focus in front of the retina, instead of on it, causing blurriness. See Figure 9.8.3[6] for a simulated image of a person’s vision with myopia. Nearsightedness usually becomes apparent between ages 6 and 14. It is corrected with glasses, contacts, or LASIK surgery.[7]

A myopic eye has too short focal distances (has too high power) so that distant objects are focused in front of the retina by the unaccommodated eye. The far point is thus not at infinity, but closer. This can be corrected by a negative lens. Suppose the far point is at 2 m. If the concave lens makes a virtual image of a distant object at distance 2 m in front of the cornea, the unaccommodated eye can see it clearly. The lens Law (2.5.44), with so=−∞ implies then fi=si=−2 m. Hence the required power of the lens is: D=1f=−0.5 Diopter.
Contact lenses are very close to the eye lens and hence the total power of the eye with a contact lens is simply the sum of the power of the eye and the contact lens.
Hyperopia
Hyperopia or Farsightedness. In this case a distant object is imaged by the unaccommodated eye behind the retina, i.e. the back focal distance of the unaccommodated eye is larger than the depth of the eye. Close objects can not be imaged on the retina, hence the near point is relatively far from the cornea. In order to bend the rays more, a positive lens is placed in front of the eye. Suppose that a hyperopic eye has near point at distance 125 cm. For an object at so=−25 cm to have virtual image at si=−125 cm, so that it can be seen, the focal length must satisfy 1f=−1so+1si=10.25−11.25=10.31,
Presbyopia
Presbyopia is impaired near vision. It commonly occurs in middle-aged and older adults, making it difficult to clearly see objects up close. As people age, the lens in the eye gets harder and less flexible and stops focusing light correctly on the retina.[8] Presbyopia results in an increase in the distance between the near point and the retina. This defect affects all images. Presbyopia is usually corrected by glasses with progressive correction, the upper part of glass used for distance vision and the lower part for near vision. . See Figure 9.8.4[9] for a simulated image of a person’s vision with presbyopia.

Astigmatism
Astigmatism. In this case the focal distances for two directions perpendicular to the optical axis are different. It is attributed to a lack of symmetry of revolution of the cornea. This is compensated by using glasses which themselves are astigmatic.
Color Blindness
Color blindness makes it difficult to differentiate between certain colors. Color blindness can occur due to damage to the eye or to the brain. There’s no cure for color blindness, but special glasses and contact lenses can help people differentiate between colors. Most people who have color blindness are able to use visual strategies related to color selection and don’t have problems participating in everyday activities.[10]
Dry Eye
Dry eye is a very common eye condition that occurs when the eyes don’t make enough tears to stay wet or the tears don’t work correctly. Symptoms of dry eye include a scratchy feeling, stinging, and burning. Treatment includes over-the-counter and prescription eye drops, as well as lifestyle changes to decrease the dryness of the eyes.[11]
Conjunctivitis
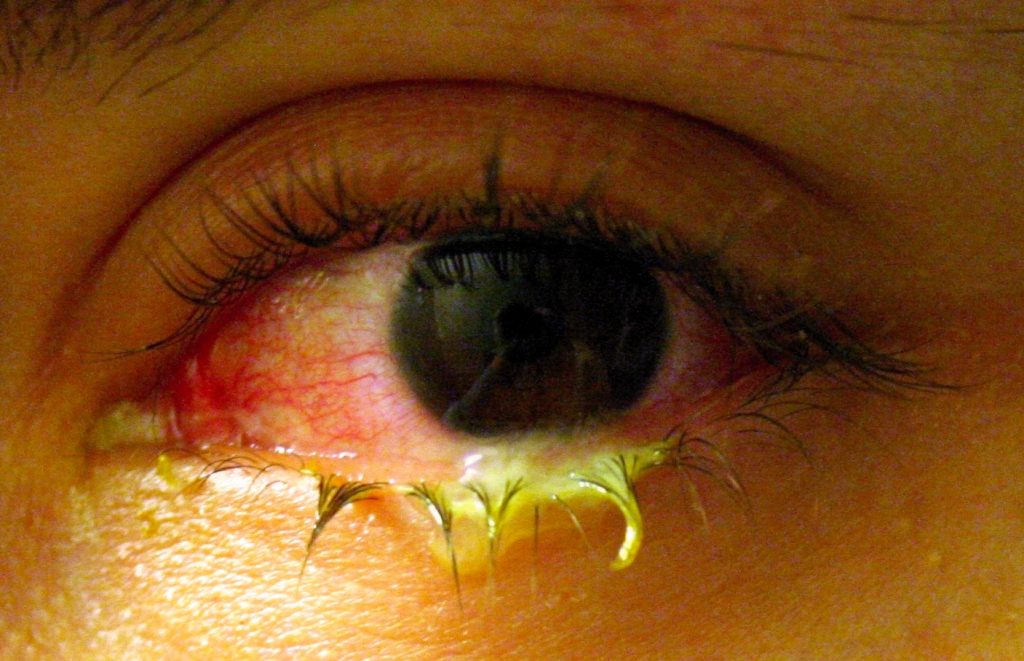
Conjunctivitis is a viral or bacterial infection that causes swelling and redness in the conjunctiva and sclera. See Figure 9.8.5[12] for an image of conjunctivitis. The eye may feel itchy and painful with crusty yellow drainage present. Conjunctivitis is very contagious, so the nurse should educate the patient and family caregivers to wash hands frequently. Additionally, the patient should not share items like pillowcases, towels, or makeup. Bacterial conjunctivitis is treated with antibiotic eye drops.[13]
Stye
A stye is a bacterial infection of an oil gland in the eyelid, causing a red, tender bump at the edge of the eyelid. See Figure 9.8.6[14] for an image of a stye. Treatment includes applying warm compresses to the eyelid and prescription eyedrops.[15]

Cataracts
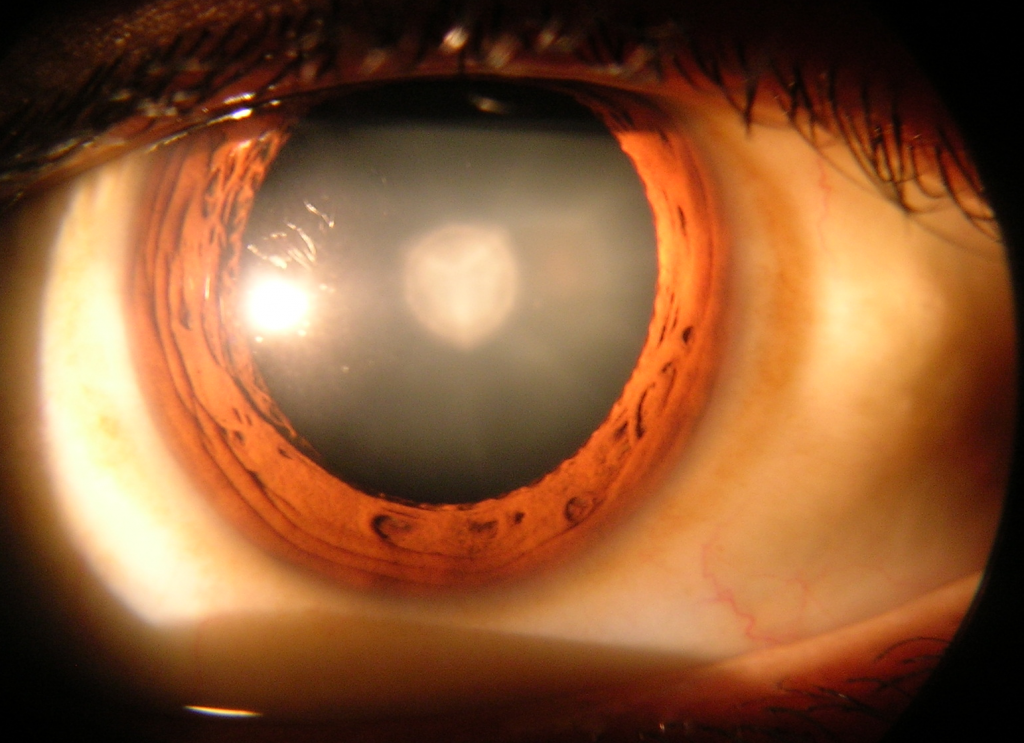
A cataract is a cloudy area on the lens of the eye. Cataracts are very common in older adults. Over half of all Americans age 80 or older either have cataracts or have had surgery to remove cataracts. See Figure 9.8.7[16] for an image of a cataract. Cataracts develop slowly and symptoms include faded colors, blurred or double vision, halos around light, and trouble seeing at night. See Figure 9.8.8[17] for a simulated image of a person’s vision with cataracts. Decreased vision due to cataracts may result in trouble reading and driving and increases the risk of falling. Patients often undergo surgery for cataracts. During cataract surgery, the doctor removes the clouded lens and replaces it with a new, artificial lens.[18]

Macular Degeneration
Age-related macular degeneration is a common condition that causes blurred central vision. It is the leading cause of vision loss for people 50 and older. See Figure 9.8.9[19] for a simulated image of a person’s vision with macular degeneration. There are two types of macular degeneration: dry (nonexudative) and wet (exudative). During dry macular degeneration, cellular debris called drusen accumulates and scars the retina. In the wet (exudative) form, which is more severe, blood vessels grow behind the retina that leak exudate fluid, causing hemorrhaging and scarring. There is no treatment for dry macular degeneration, but laser therapy can be used to help treat wet (exudative) macular degeneration.[20]

Glaucoma
Glaucoma is a group of eye diseases that causes vision loss by damaging the optic nerve due to increased intraocular pressure. Treatment includes prescription eye drops to lower the pressure inside the eye and slow the progression of the disease. If not treated appropriately, glaucoma can cause blindness. Symptoms of glaucoma include gradual loss of peripheral vision. See Figure 9.8.10[21] for a simulated image of a person’s vision with glaucoma. Because the loss of vision occurs so slowly, many people don’t realize they have symptoms until the disease is well-progressed or it is discovered during an eye exam.[22]

Screening Tools for Eye Exams
Common screening tools used during an eye exam are the Snellen chart, a near vision chart, and Ishihara plates. Nurses working in outpatient settings or school settings use these tools when screening patients for vision problems. If a vision problem is identified, the patient is referred to an optometrist for further testing. When performing a vision assessment, be sure to provide adequate lighting.
Snellen Chart
Distant vision is tested by using the Snellen chart. See Figure 9.8.11[23] for an image of the Snellen chart. Place the patient 20 feet away from the Snellen chart. Ask them to cover one eye and read the letters from the lowest line they can see clearly. Record the corresponding fraction in the furthermost right-hand column. Repeat with the other eye. If the patient is wearing glasses or contact lens during this assessment, document the results as “corrected vision” when wearing these assistive devices.
A person with no visual impairment is documented as having 20/20 vision. A person with impaired vision has a different lower denominator of this fraction. For example, a vision measurement of 20/30 indicates the patient can see letters clearly at 20 feet that a person with normal vision can see clearly at 30 feet.[24] Alternative charts are also available for children or adults who can’t read letters in English. See Figure 9.8.12[25]for an alternative eye chart.


Near Vision
Near vision is assessed by having a patient read from a prepared card that is held 14 inches away from the eyes. If a card is not available, the patient can be asked to read from a newspaper as an alternative quick screening tool. See Figure 9.8.13[26] for an image of a prepared card used to assess near vision.

Ishihara Plates
Ishihara plates are commonly used to assess color vision. Each of the colored dotted plates shows either a number or a path. See Figure 9.8.14[27]for an example of Ishihara plates. A person with color blindness is not able to distinguish the numbers or paths from the other colored dots on the plate.

New Correction Technique
In recent years, to correct eye defects such as myopia and astigmatism, technology has been developed to change the local curvatures of the surface of the cornea using an excimer laser. The laser is computer-controlled and causes photo-ablation in parts of the cornea.


