2.7.7: Solving Linear Equations and Inequalities
- Page ID
- 73989
By the end of this section, you will be able to:
- Solve equations using a general strategy
- Solve inequalities using the Subtraction and Addition Properties of inequality
- Solve inequalities using the Division and Multiplication Properties of inequality
- Solve inequalities that require simplification
- Translate to an inequality and solve
It is time now to lay out one overall strategy that can be used to solve any linear equation. Some equations we solve will not require all these steps to solve, but many will.
Beginning by simplifying each side of the equation makes the remaining steps easier.
Solve: \(-6(x + 3) = 24\).
- Answer
-





- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution. Substitute the solution into the original equation to make sure the result is a true statement.
Solve: \(-(y + 9) = 8\)
- Answer
-
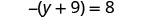
Simplify each side of the equation as much as possible by distributing. 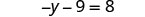
The only y term is on the left side, so all variable terms are on the left side of the equation. Add 9 to both sides to get all constant terms on the right side of the equation. 
Simplify. 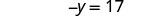
Rewrite −y as −1y. 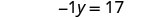
Make the coefficient of the variable term to equal to 1 by dividing both sides by −1. 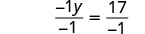
Simplify. 
Check: 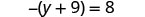
Let y=−17. 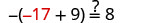
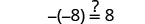
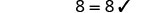
Solve: \(5(a - 3) + 5 = -10\)
- Answer
-

Simplify each side of the equation as much as possible. Distribute. 
Combine like terms. 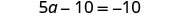
The only a term is on the left side, so all variable terms are on one side of the equation. Add 10 to both sides to get all constant terms on the other side of the equation. 
Simplify. 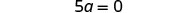
Make the coefficient of the variable term to equal to 11 by dividing both sides by 55. 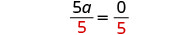
Simplify. 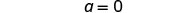
Check: 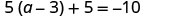
Let a=0. 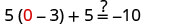
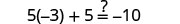
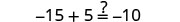
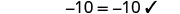
Solve: \(\frac{2}{3}(6m - 3) = 8 - m\)
- Answer
-
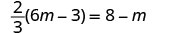
Distribute. 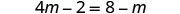
Add m to get the variables only to the left. 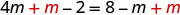
Simplify. 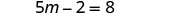
Add 2 to get constants only on the right. 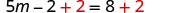
Simplify. 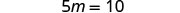
Divide by 5. 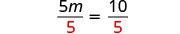
Simplify. 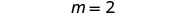
Check: 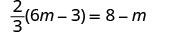
Let m=2. 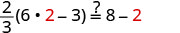
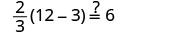
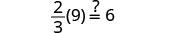
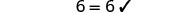
Solve: \(8 - 2(3y + 5) = 0\)
- Answer
-
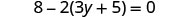
Simplify—use the Distributive Property. 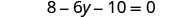
Combine like terms. 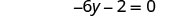
Add 2 to both sides to collect constants on the right. 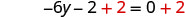
Simplify. 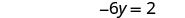
Divide both sides by −6−6. 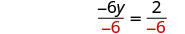
Simplify. 
Check: Let y=−13.
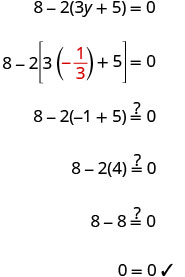
Solve: \(4(x - 1)-2=5(2x+3)+6\)
- Answer
-
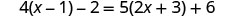
Distribute. 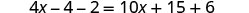
Combine like terms. 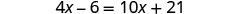
Subtract 4x to get the variables only on the right side since \(10>4\). 
Simplify. 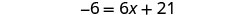
Subtract 21 to get the constants on left. 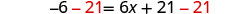
Simplify. 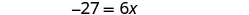
Divide by 6. 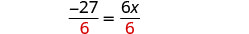
Simplify. 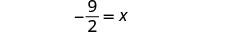
Check: 
Let \(x=-\frac{9}{2}\). 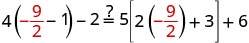
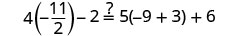
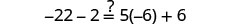
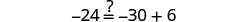
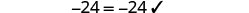
Solve: \(10[3 - 8(2s-5)] = 15(40 - 5s)\)
- Answer
-
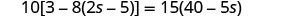
Simplify from the innermost parentheses first. 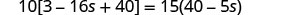
Combine like terms in the brackets. 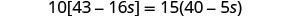
Distribute. 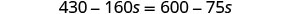
Add 160s to get the s’s to the right. 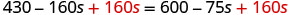
Simplify. 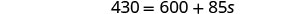
Subtract 600 to get the constants to the left. 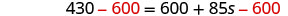
Simplify. 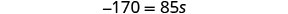
Divide. 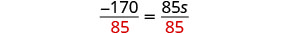
Simplify. 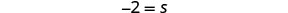
Check: 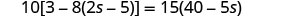
Substitute s=−2. 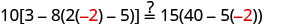
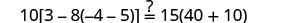
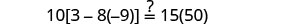
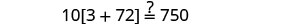
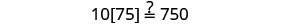
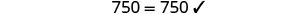
Solve: \(0.36(100n+5)=0.6(30n+15)\).
- Answer
-
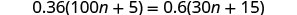
Distribute. 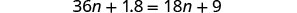
Subtract 18n to get the variables to the left. 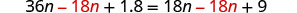
Simplify. 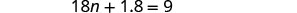
Subtract 1.8 to get the constants to the right. 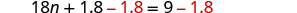
Simplify. 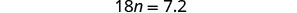
Divide. 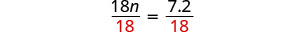
Simplify. 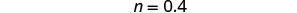
Check: 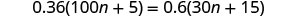
Let n=0.4. 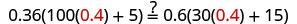
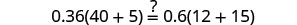
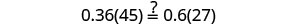
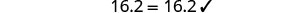
Use the Distance, Rate, and Time Formula
One formula you will use often in algebra and in everyday life is the formula for distance traveled by an object moving at a constant rate. Rate is an equivalent word for “speed.” The basic idea of rate may already familiar to you. Do you know what distance you travel if you drive at a steady rate of 60 miles per hour for 2 hours? (This might happen if you use your car’s cruise control while driving on the highway.) If you said 120 miles, you already know how to use this formula!
For an object moving at a uniform (constant) rate, the distance traveled, the elapsed time, and the rate are related by the formula:
\[\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}\]
We will use the Strategy for Solving Applications that we used earlier in this chapter. When our problem requires a formula, we change Step 4. In place of writing a sentence, we write the appropriate formula. We write the revised steps here for reference.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. Write the appropriate formula for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
You may want to create a mini-chart to summarize the information in the problem. See the chart in this first example.
Jamal rides his bike at a uniform rate of 12 miles per hour for \(3\frac{1}{2}\) hours. What distance has he traveled?
- Answer
-
Step 1. Read the problem. Step 2. Identify what you are looking for. distance traveled Step 3. Name. Choose a variable to represent it. Let d = distance. Step 4. Translate: Write the appropriate formula. \(d=rt\) 
Substitute in the given information. \(d = 12\cdot 3\frac{1}{2}\) Step 5. Solve the equation. \(d=42\text{ miles}\) Step 6. Check Does 42 miles make sense? Jamal rides: 
Step 7. Answer the question with a complete sentence. Jamal rode 42 miles.
Rey is planning to drive from his house in San Diego to visit his grandmother in Sacramento, a distance of 520 miles. If he can drive at a steady rate of 65 miles per hour, how many hours will the trip take?
- Answer
-
Step 1. Read the problem. Step 2. Identify what you are looking for. How many hours (time) Step 3. Name.
Choose a variable to represent it.Let t = time. 
Step 4. Translate.
Write the appropriate formula.\(d=rt\) Substitute in the given information. \(520 = 65t\) Step 5. Solve the equation. \(t = 8\) Step 6. Check. Substitute the numbers into
the formula and make sure the result is a
true statement.\(\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array}\) Step 7. Answer the question with a complete sentence. Rey’s trip will take 8 hours.
Solve a Formula for a Specific Variable
You are probably familiar with some geometry formulas. A formula is a mathematical description of the relationship between variables. Formulas are also used in the sciences, such as chemistry, physics, and biology. In medicine they are used for calculations for dispensing medicine or determining body mass index. Spreadsheet programs rely on formulas to make calculations. It is important to be familiar with formulas and be able to manipulate them easily.
In Exercise \(\PageIndex{1}\) and Exercise \(\PageIndex{4}\), we used the formula \(d=rt\). This formula gives the value of d, distance, when you substitute in the values of r and t, the rate and time. But in Exercise \(\PageIndex{4}\), we had to find the value of t. We substituted in values of d and r and then used algebra to solve for tt. If you had to do this often, you might wonder why there is not a formula that gives the value of t when you substitute in the values of d and r. We can make a formula like this by solving the formula \(d=rt\) for t.
To solve a formula for a specific variable means to isolate that variable on one side of the equals sign with a coefficient of 1. All other variables and constants are on the other side of the equals sign. To see how to solve a formula for a specific variable, we will start with the distance, rate and time formula.
Solve the formula d=rt for t:
- when d=520 and r=65
- in general
- Answer
-
We will write the solutions side-by-side to demonstrate that solving a formula in general uses the same steps as when we have numbers to substitute.
1. when d=520 and r=65 2. in general Write the formula. \(d=rt\) Write the formula. \(d=rt\) Substitute. \(520=65t\) Divide, to isolate t. \(\frac{520}{65} = \frac{65t}{65}\) Divide, to isolate tt. \(\frac{d}{r} = \frac{rt}{t}\) Simplify. \(8 = t\) Simplify. \(\frac{d}{r}=t\) We say the formula \(t = \frac{d}{r}\) is solved for t.
Solve the formula \(A = \frac{1}{2}bh\) for h:
- when \(A = 90\) and \(b = 15\)
- in general
- Answer
-
We can now find the height of a triangle, if we know the area and the base, by using the formula \(h = \frac{2A}{b}\)1. when \(A = 90\) and \(b = 15\) 2. in general Write the formula. 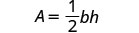
Write the formula. 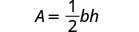
Substitute. 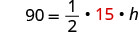
Clear the fractions. 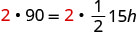
Clear the fractions. 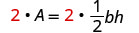
Simplify. 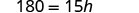
Simplify. 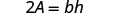
Solve for h. 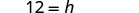
Solve for hh. 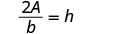
The formula \(I=Prt\) is used to calculate simple interest, I, for a principal, P, invested at rate, r, for t years.
Solve the formula I=Prt to find the principal, P:
- when I=$5,600, r=4% ,t=7years
- in general
- Answer
-
1. I=$5,600, r=4% ,t=7years 2. in general Write the formula. 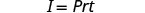
Write the formula. 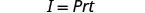
Substitute. 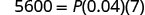
Simplify. 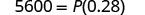
Simplify. 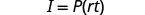
Divide, to isolate P. 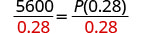
Divide, to isolate P. 
Simplify. 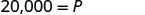
Simplify. 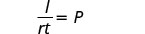
The principal is 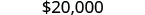
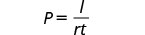
Later in this class, and in future algebra classes, you’ll encounter equations that relate two variables, usually x and y. You might be given an equation that is solved for y and need to solve it for x, or vice versa. In the following example, we’re given an equation with both x and y on the same side and we’ll solve it for y.
Solve the formula 3x+2y=18 for y:
- when x=4
- in general
- Answer
-
1. when x=4 2. in general 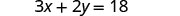
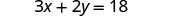
Substitute. 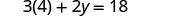
Subtract to isolate the
y-term.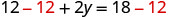
Subtract to isolate the
y-term.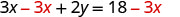
Divide. 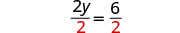
Divide. 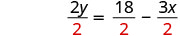
Simplify. 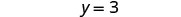
Simplify. 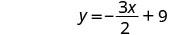
In Exercise \(\PageIndex{7}\) through Exercise \(\PageIndex{18}\) we used the numbers in part 1 as a guide to solving in general in part 2. Now we will solve a formula in general without using numbers as a guide.
Solve the formula P=a+b+c for a.
- Answer
-
We will isolate aa on one side of the equation. 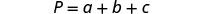
Both b and c are added to a, so we subtract them from both sides of the equation. 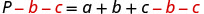
Simplify. 
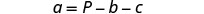
Solve the formula 6x+5y=13 for y.
- Answer
-
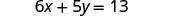
Subtract 6x from both sides to isolate the term with y. 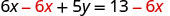
Simplify. 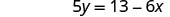
Divide by 5 to make the coefficient 1. 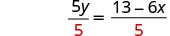
Simplify. 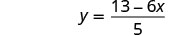
The fraction is simplified. We cannot divide 13−6x by 5.
Solve Inequalities using the Subtraction and Addition Properties of Inequality
The Subtraction and Addition Properties of Equality state that if two quantities are equal, when we add or subtract the same amount from both quantities, the results will be equal.
\[\begin{array} { l l } { \textbf { Subtraction Property of Equality } } & { \textbf { Addition Property of Equality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if } \qquad \quad a = b , } & { \text { if } \qquad \quad a = b } \\ { \text { then } a - c = b - c . } & { \text { then } a + c = b + c } \end{array}\]
Similar properties hold true for inequalities.
| For example, we know that −4 is less than 2. | 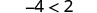 |
| If we subtract 5 from both quantities, is the left side still less than the right side? | 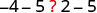 |
| We get −9 on the left and −3 on the right. |  |
| And we know −9 is less than −3. |  |
|
The inequality sign stayed the same. |
Similarly we could show that the inequality also stays the same for addition.
This leads us to the Subtraction and Addition Properties of Inequality.
\[\begin{array} { l l } { \textbf { Subtraction Property of Inequality } } & { \textbf { Addition Property of Inequality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if }\qquad \quad a < b } & { \text { if } \qquad \quad a < b } \\ { \text { then } a - c < b - c . } & { \text { then } a + c < b + c } \\\\ { \text { if } \qquad \quad a > b } & { \text { if } \qquad \quad a > b } \\ { \text { then } a - c > b - c . } & { \text { then } a + c > b + c } \end{array}\]
We use these properties to solve inequalities, taking the same steps we used to solve equations. Solving the inequality \(x+5>9\), the steps would look like this:
\[\begin{array}{rrll} {} &{x + 5} &{ >} &{9} \\ {\text{Subtract 5 from both sides to isolate }x.} &{x + 5 - 5} &{ >} &{9 - 5} \\{} &{x} &{ >} &{4} \\ \end{array}\]
Any number greater than 4 is a solution to this inequality.
Solve the inequality \(n - \frac{1}{2} \leq \frac{5}{8}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
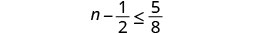
Add \(\frac{1}{2}\) to both sides of the inequality. 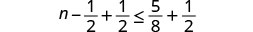
Simplify. 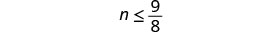
Graph the solution on the number line. 
Write the solution in interval notation.
Solve Inequalities using the Division and Multiplication Properties of Inequality
The Division and Multiplication Properties of Equality state that if two quantities are equal, when we divide or multiply both quantities by the same amount, the results will also be equal (provided we don’t divide by 0).
\[\begin{array}{ll} {\textbf{Division Property of Equality}} &{\textbf{MUltiplication Property of Equality}} \\ {\text{For any numbers a, b, c, and c} \neq 0} &{\text{For any numbers a, b, c}} \\ {\text{if } \qquad a = b} &{\text{if} \qquad \quad a = b} \\ {\text{then }\quad \frac{a}{c} = \frac{b}{c}} &{\text{then } \quad ac = bc} \end{array}\]
Are there similar properties for inequalities? What happens to an inequality when we divide or multiply both sides by a constant?
Consider some numerical examples.
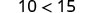 |
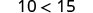 |
||
| Divide both sides by 5. | 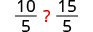 |
Multiply both sides by 5. |  |
| Simplify. |  |
 |
|
| Fill in the inequality signs. |  |
 |
The inequality signs stayed the same.
Does the inequality stay the same when we divide or multiply by a negative number?
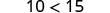 |
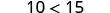 |
||
| Divide both sides by -5. | 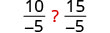 |
Multiply both sides by -5. |  |
| Simplify. |  |
 |
|
| Fill in the inequality signs. |  |
 |
The inequality signs reversed their direction.
When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.
Here are the Division and Multiplication Properties of Inequality for easy reference.
For any real numbers a,b,c
\[\begin{array}{ll} {\text{if } a < b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \\ {\text{if } a > b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a < b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a > b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \end{array}\]
When we divide or multiply an inequality by a:
- positive number, the inequality stays the same.
- negative number, the inequality reverses.
Solve the inequality \(7y<42\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
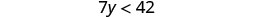
Divide both sides of the inequality by 7.
Since \(7>0\), the inequality stays the same.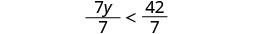
Simplify. 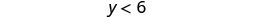
Graph the solution on the number line. 
Write the solution in interval notation. 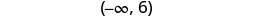
Solve the inequality \(−10a\geq 50\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
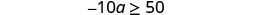
Divide both sides of the inequality by −10.
Since \(−10<0\), the inequality reverses.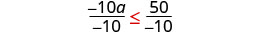
Simplify. 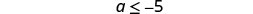
Graph the solution on the number line. 
Write the solution in interval notation. 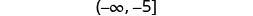
Sometimes when solving an inequality, the variable ends up on the right. We can rewrite the inequality in reverse to get the variable to the left.
\[\begin{array}{l} x > a\text{ has the same meaning as } a < x \end{array}\]
Think about it as “If Xavier is taller than Alex, then Alex is shorter than Xavier.”
Solve the inequality \(-20 < \frac{4}{5}u\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
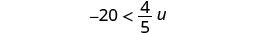
Multiply both sides of the inequality by \(\frac{5}{4}\).
Since \(\frac{5}{4} > 0\), the inequality stays the same.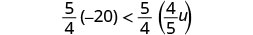
Simplify. 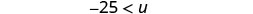
Rewrite the variable on the left. 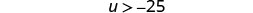
Graph the solution on the number line. 
Write the solution in interval notation. 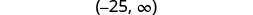
Solve the inequality \(\frac{t}{-2} \geq 8\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
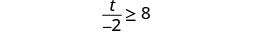
Multiply both sides of the inequality by −2.
Since \(−2<0\), the inequality reverses.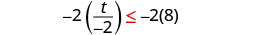
Simplify. 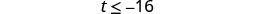
Graph the solution on the number line. 
Write the solution in interval notation. 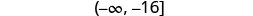
Solve Inequalities That Require Simplification
Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but be sure to pay close attention during multiplication or division.
Solve the inequality \(4m\leq 9m+17\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
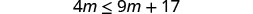
Subtract 9m from both sides to collect the variables on the left. 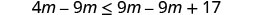
Simplify. 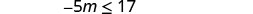
Divide both sides of the inequality by −5, and reverse the inequality. 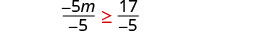
Simplify. 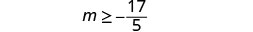
Graph the solution on the number line. 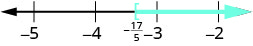
Write the solution in interval notation. 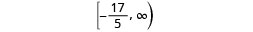
Solve the inequality \(8p+3(p−12)>7p−28\) graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Simplify each side as much as possible. 8p+3(p−12)>7p−28 Distribute. 8p+3p−36>7p−28 Combine like terms. 11p−36>7p−28 Subtract 7p from both sides to collect the variables on the left. 11p−36−7p>7p−28−7p Simplify. 4p−36>−28 Add 36 to both sides to collect the constants on the right. 4p−36+36>−28+36 Simplify. 4p>8 Divide both sides of the inequality by 4; the inequality stays the same. \(\frac{4p}{4}>84\) Simplify. \(p>2\) Graph the solution on the number line. 
Write the solution in interval notation. \((2, \infty)\)
Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.
Solve the inequality \(8x−2(5−x)<4(x+9)+6x\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Simplify each side as much as possible. 8x−2(5−x)<4(x+9)+6x Distribute. 8x−10+2x<4x+36+6x Combine like terms. 10x−10<10x+36 Subtract 10x from both sides to collect the variables on the left. 10x−10−10x<10x+36−10x Simplify. −10<36 The xx’s are gone, and we have a true statement. The inequality is an identity.
The solution is all real numbers.Graph the solution on the number line. 
Write the solution in interval notation. \((-\infty, \infty)\)
Solve the inequality \(\frac{1}{3}a - \frac{1}{8}a > \frac{5}{24}a + \frac{3}{4}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
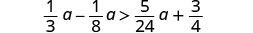
Multiply both sides by the LCD, 24, to clear the fractions. 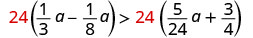
Simplify. 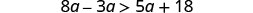
Combine like terms. 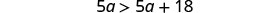
Subtract 5a from both sides to collect the variables on the left. 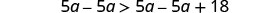
Simplify. 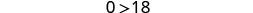
The statement is false! The inequality is a contradiction. There is no solution. Graph the solution on the number line. 
Write the solution in interval notation. There is no solution.
Translate to an Inequality and Solve
To translate English sentences into inequalities, we need to recognize the phrases that indicate the inequality. Some words are easy, like ‘more than’ and ‘less than’. But others are not as obvious.
Think about the phrase ‘at least’ – what does it mean to be ‘at least 21 years old’? It means 21 or more. The phrase ‘at least’ is the same as ‘greater than or equal to’.
Table \(\PageIndex{4}\) shows some common phrases that indicate inequalities.
| > | \(\geq\) | < | \(\leq\) |
|---|---|---|---|
| is greater than | is greater than or equal to | is less than | is less than or equal to |
| is more than | is at least | is smaller than | is at most |
| is larger than | is no less than | has fewer than | is no more than |
| exceeds | is the minimum | is lower than | is the maximum |
Translate and solve. Then write the solution in interval notation and graph on the number line.
Twelve times c is no more than 96.
- Answer
-
Translate. 
Solve—divide both sides by 12. 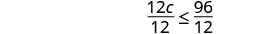
Simplify. 
Write in interval notation. 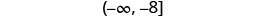
Graph on the number line. 
Translate and solve. Then write the solution in interval notation and graph on the number line.
Thirty less than x is at least 45.
- Answer
-
Translate. 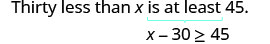
Solve—add 30 to both sides. 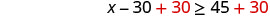
Simplify. 
Write in interval notation. 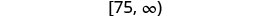
Graph on the number line. 
Key Concepts
- General Strategy for Solving Linear Equations
- Simplify each side of the equation as much as possible.
Use the Distributive Property to remove any parentheses.
Combine like terms. - Collect all the variable terms on one side of the equation.
Use the Addition or Subtraction Property of Equality. - Collect all the constant terms on the other side of the equation.
Use the Addition or Subtraction Property of Equality. - Make the coefficient of the variable term to equal to 1.
Use the Multiplication or Division Property of Equality.
State the solution to the equation. - Check the solution.
Substitute the solution into the original equation.
- Simplify each side of the equation as much as possible.


