5.7.1: Overview
- Last updated
- Mar 8, 2021
- Save as PDF
- Page ID
- 33966

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Interpret the circulatory system in terms of your knowledge of fluid dynamics
We have discussed many situations in which fluids are static, though there are many situations where fluids flow. For example, a column of smoke rises from a camp fire, water streams from a fire hose, blood courses through your veins. Why does rising smoke curl and twist? How does a nozzle increase the speed of water emerging from a hose? How does the body regulate blood flow? Fluid dynamics, the physics of fluids in motion, allows us to answer these and many other questions.
Application in the Circulatory System
For example, consider the circulatory system—a connected series of tubes with fluid flowing through them. The heart is the driver of the circulatory system, generating cardiac output (CO) by rhythmically contracting and relaxing. This creates changes in regional pressures and (combined with a complex valvular system in the heart and the veins) ensures that the blood moves around the circulatory system in one direction. The “beating” of the heart generates pulsatile blood flow, conducted into the arteries across the micro-circulation and then back via the venous system to the heart.
The aorta, the main artery, leaves the left side of the heart and proceeds to divide into smaller and smaller arteries that first become arterioles and eventually become capillaries, through which oxygen transfer occurs. The capillaries connect to venules, into which the deoxygenated blood passes from the cells back into the blood. The blood then travels back through the network of veins to the right heart. The micro-circulation (arterioles, capillaries and venules) constitutes most of the area of the vascular system and is the site of the transfer of O2 into the cells.
The venous system returns the de-oxygenated blood to the right heart where it is pumped into the lungs to become oxygenated. This is also where CO2 and other gaseous wastes are exchanged and expelled during breathing. Blood then returns to the left side of the heart where it begins the process again. The heart, vessels and lungs are all actively involved in maintaining healthy cells and organs, and all influence the fluid dynamics of the blood.
Fluids and Diffusion
Now consider how nutrients are transported through a human body. Diffusion is the movement of substances due to random thermal molecular motion. Fluids can even diffuse through solids (such as fumes or odors entering ice cubes). Diffusion is the dominant mechanism by which the exchange of nutrients and waste products occurs between the blood and tissue, and between air and blood in the lungs. In the evolutionary process, as organisms became larger they needed quicker methods of transportation than net diffusion, due to the larger distances involved in the transport. This factor lead to the development of circulatory systems. Less sophisticated, single-celled organisms still rely totally on diffusion for the removal of waste products and the uptake of nutrients.
Another important form of fluid movement is osmosis—the transport of water through a semipermeable membrane (shown in ) from a region of high concentration to a region of low concentration. It is driven by the imbalance in water concentration. Similarly, dialysis is the transport of any other molecule through a semipermeable membrane due to its concentration difference. Both osmosis and dialysis are used by the kidneys to cleanse the blood, and the medical application of dialysis through machinery is important in the treatment of individuals with failing kidney function.
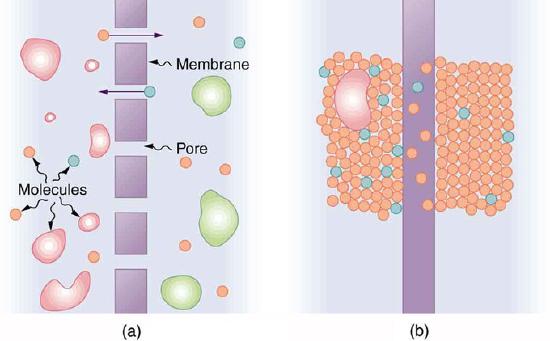
A Semipermeable Membrane: A semipermeable membrane with small pores that allow only small molecules to pass through.
Flow Rate and Velocity
Flow velocity and volumetric flow rates are important quantities in fluid dynamics used to quantify motion of a fluid and are interrelated.
learning objectives
- Assess the significance of studying volumetric flow in addition to flow velocity
Fluid dynamics is the study of fluids in motion and corresponding phenomena. A fluid in motion has a velocity, just as a solid object in motion has a velocity. Like the velocity of a solid, the velocity of a fluid is the rate of change of position per unit of time. In mathematical terms, the velocity of a fluid is the derivative of the position vector of the fluid with respect to time, and is therefore itself a vector quantity. The flow velocity vector is a function of position, and if the velocity of the fluid is not constant then it is also a function of time. Equation 1 shows the mathematical expression for the velocity of a fluid in motion. As a vector quantity, fluid velocity must have at least one non-zero directional component and may have up to three non-zero directional components. The velocity vector has non-zero components in any orthogonal direction along which motion of the fluid occurs.
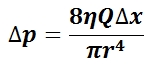
Flow Velocity: Mathematical Expression for Flow Velocity
Turbulent Flow vs. Laminar Flow
Fluid velocity can be affected by the pressure of the fluid, the viscosity of the fluid, and the cross-sectional area of the container in which the fluid is travelling. These factors affect fluid velocity depending on the nature of the fluid flow—particularly whether the flow is turbulent or laminar in nature. In the case of turbulent flow, the flow velocity is complex in nature and thus hard to predict; it must be analyzed on a system per system basis. In the case of Laminar flow, however, fluid flow is much simpler and flow velocity can be accurately calculated using Poiseuille’s Law. In SI units, fluid flow velocity is expressed in terms of meters per seconds. The magnitude of the fluid flow velocity is the fluid flow speed. Fluid flow velocity effectively describes everything about the motion of a fluid.
Volumetric Flow
In addition to flow velocity, volumetric flow rate is an important quantity in fluid dynamics analysis. Volumetric flow is defined as the volume of fluid that passes through a given surface per unit time. Qualitatively, Figure 1 shows the notion of volumetric flow rate regarding a cross-sectional surface of area A. Mathematically, volumetric flow rate is the derivative of the volume of fluid that passes through a given surface with respect to time; in SI units this is expressed as meterscubed per second. Volumetric flow rate is related to the flow velocity vector as the surface integral with respect to the surface in question. If the surface area in question is a flat, plane cross-section, the surface integral reduces as shown in Equation 2, where A is the surface area of the surface in question and v is the flow velocity of the fluid.
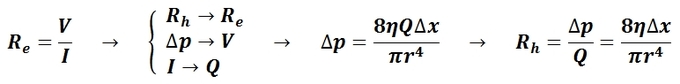
Volumetric Flow Rate: Volumetric Flow Rate Surface Integral and its simplification
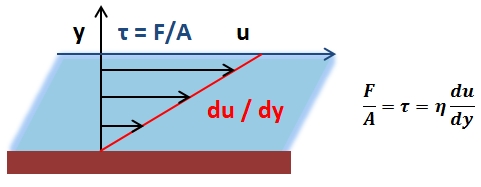
Flow Velocity – Volumetric Flow Rate Relation: This figure shows the relation between flow velocity and volumetric flow rate.
Moreover, only the flow velocity component parallel to the surface normal of the surface in question, or alternatively the flow velocity component perpendicular to the surface in question contributes to the volumetric flow rate. Figure 1 and Equation 2 illustrate decomposition of the flow velocity vector, making an angle θ with respect to the normal of the surface plane in order to calculate volumetric flow rate through that surface. Thus, volumetric flow rate for a given fluid velocity and cross-sectional surface area increases as θ decreases, and is maximized when θ = 0. Volumetric flow rate is an important scalar quantity in fluid dynamics and is used widely in fluid flow measurements. Volumetric flow rate can be converted to mass flow rate if the density of the fluid is known. Flow of fluids through a closed system is often analyzed as a hydraulic circuit analogous to electron flow in an electronic circuit where: 1) the volumetric fluid flow is analogous to the electric current, 2) pressure is analogous to the voltage, and 3) fluid velocity is analogous to current density.
Key Points
- There are many fluids in biology and understanding their behavior in motion is crucial to effective medicine.
- The heart pumps a fluid, blood, throughout a series of tubes in the body.
- Circulation may be understood through a study of fluid dynamics.
- Diffusion is the dominant mechanism by which the exchange of nutrients and waste products occur between the blood and tissue, and between air and blood in the lungs.
- Both osmosis and dialysis are used by the kidneys to cleanse the blood, and the medical application of dialysis through machinery is important in the treatment of individuals with failing kidney function.
- Flow velocity is a vector quantity used to describe the motion of a fluid. It can be easily determined for laminar flow but complex to determine for turbulent flow.
- Volumetric flow rate is the volume of a liquid that passes through a given surface per unit time. It is found from the flow velocity and the surface area of the surface through which the fluid passes.
- Fluid flow through a closed hydraulic system is analyzed much like electron flow through an electronic circuit —where volumetric flow rate is analogous to current, flow velocity is analogous to current density, and pressure is analogous to voltage (electrical potential).
Key Terms
- vascular: Of, pertaining to, or containing vessels that conduct or circulate fluids (such as blood, lymph, or sap) through the body of an animal or plant.
- osmosis: The net movement of solvent molecules from a region of high solvent potential to a region of lower solvent potential through a partially permeable membrane.
- dialysis: A method of separating molecules or particles of different sizes by differential diffusion through a semipermeable membrane.
- Laminar Flow: Non-turbulent motion of a fluid in which parallel layers have different velocities relative to each other.
- Turbulent Flow: The motion of a fluid having local velocities and pressures that fluctuate randomly.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42212/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42212/latest/?collection=col11406/1.7. License: CC BY: Attribution
- OpenStax College, Introduction to Fluid Dynamics and Its Biological and Medical Applications. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42204/latest/. License: CC BY: Attribution
- Haemodynamics. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Haemodynamics. License: CC BY-SA: Attribution-ShareAlike
- dialysis. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/dialysis. License: CC BY-SA: Attribution-ShareAlike
- osmosis. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/osmosis. License: CC BY-SA: Attribution-ShareAlike
- vascular. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/vascular. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. March 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42212/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Flow measurement). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Flow_measurement). License: CC BY-SA: Attribution-ShareAlike
- Flow measurement. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Flow_measurement. License: CC BY-SA: Attribution-ShareAlike
- Volumetric flow rate. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Volumetric_flow_rate. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/turbulent-flow. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/laminar-flow. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. March 2, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42212/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike
- Provided by: N/A. Located at: N/A. License: CC BY-SA: Attribution-ShareAlike

