10.9: Conservation of Angular Momentum
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18016

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Evaluate the implications of net torque on conservation of energy
Let us consider some examples of momentum: the Earth continues to spin at the same rate it has for billions of years; a high-diver who is “rotating” when jumping off the board does not need to make any physical effort to continue rotating, and indeed would be unable to stop rotating before hitting the water. These examples have the hallmarks of a conservation law. Following are further observations to consider:
- A closed system is involved. Nothing is making an effort to twist the Earth or the high-diver. They are isolated from rotation changing influences (hence the term “closed system”).
- Something remains unchanged. There appears to be a numerical quantity for measuring rotational motion such that the total amount of that quantity remains constant in a closed system.
- Something can be transferred back and forth without changing the total amount. A diver rotates faster with arms and legs pulled toward the chest from a fully stretched posture.
Angular Momentum
The conserved quantity we are investigating is called angular momentum. The symbol for angular momentum is the letter L. Just as linear momentum is conserved when there is no net external forces, angular momentum is constant or conserved when the net torque is zero. We can see this by considering Newton’s 2nd law for rotational motion:
→τ=d→Ldt, where τ is the torque. For the situation in which the net torque is zero, d→Ldt=0.
If the change in angular momentum ΔL is zero, then the angular momentum is constant; therefore,
→L=constant (when net τ=0).
This is an expression for the law of conservation of angular momentum.
Example and Implications
An example of conservation of angular momentum is seen in an ice skater executing a spin, as shown in. The net torque on her is very close to zero, because 1) there is relatively little friction between her skates and the ice, and 2) the friction is exerted very close to the pivot point.
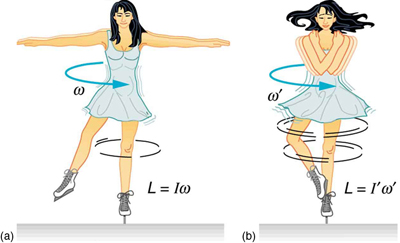
Conservation of Angular Momentum: An ice skater is spinning on the tip of her skate with her arms extended. Her angular momentum is conserved because the net torque on her is negligibly small. In the next image, her rate of spin increases greatly when she pulls in her arms, decreasing her moment of inertia. The work she does to pull in her arms results in an increase in rotational kinetic energy.
(Both F and r are small, and so →τ=→r×→F is negligibly small. ) Consequently, she can spin for quite some time. She can also increase her rate of spin by pulling in her arms and legs. When she does this, the rotational inertia decreases and the rotation rate increases in order to keep the angular momentum L=Iω constant. (I: rotational inertia, ω: angular velocity)
Conservation of angular momentum is one of the key conservation laws in physics, along with the conservation laws for energy and (linear) momentum. These laws are applicable even in microscopic domains where quantum mechanics governs; they exist due to inherent symmetries present in nature.
Conservation of Angular Momentum Theory: What it do?
Rotational Collisions
In a closed system, angular momentum is conserved in a similar fashion as linear momentum.
learning objectives
- Evaluate the difference in equation variables in rotational versus angular momentum
During a collision of objects in a closed system, momentum is always conserved. This fact is readily seen in linear motion. When an object of mass m and velocity v collides with another object of mass m2 and velocity v2, the net momentum after the collision, mv1f + mv2f, is the same as the momentum before the collision, mv1i + mv2i.
What if an rotational component of motion is introduced? Is momentum still conserved ?

Bowling ball and pi: When a bowling ball collides with a pin, linear and angular momentum is conserved
Yes. For objects with a rotational component, there exists angular momentum. Angular momentum is defined, mathematically, as L=Iω, or L=r×p. This equation is an analog to the definition of linear momentum as p=mv. Units for linear momentum are kg⋅m/s while units for angular momentum are kg⋅m2/s. As we would expect, an object that has a large moment of inertia I, such as Earth, has a very large angular momentum. An object that has a large angular velocity ω, such as a centrifuge, also has a rather large angular momentum.
So rotating objects that collide in a closed system conserve not only linear momentum p in all directions, but also angular momentum L in all directions.
For example, take the case of an archer who decides to shoot an arrow of mass m1 at a stationary cylinder of mass m2 and radius r, lying on its side. If the archer releases the arrow with a velocity v1i and the arrow hits the cylinder at its radial edge, what’s the final momentum ?
Arrow hitting cyclinde: The arrow hits the edge of the cylinder causing it to roll.
Initially, the cylinder is stationary, so it has no momentum linearly or radially. Once the arrow is released, it has a linear momentum p=m1i and an angular component relative to the cylinders rotating axis, L=rp=rm1v1i. After the collision, the arrow sticks to the rolling cylinder and the system has a net angular momentum equal to the original angular momentum of the arrow before the collision.
Key Points
- When an object is spinning in a closed system and no external torques are applied to it, it will have no change in angular momentum.
- The conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs close to the vertical axis of rotation.
- If the net torque is zero, then angular momentum is constant or conserved.
- Angular momentum is defined, mathematically, as L=Iω, or L=r×p. Which is the moment of inertia times the angular velocity, or the radius of the object crossed with the linear momentum.
- In a closed system, angular momentum is conserved in all directions after a collision.
- Since momentum is conserved, part of the momentum in a collision may become angular momentum as an object starts to spin after a collision.
Key Items
- quantum mechanics: The branch of physics that studies matter and energy at the level of atoms and other elementary particles; it substitutes probabilistic mechanisms for classical Newtonian ones.
- torque: A rotational or twisting effect of a force; (SI unit newton-meter or Nm; imperial unit foot-pound or ft-lb)
- angular momentum: A vector quantity describing an object in circular motion; its magnitude is equal to the momentum of the particle, and the direction is perpendicular to the plane of its circular motion.
- momentum: (of a body in motion) the product of its mass and velocity.
- rotation: The act of turning around a centre or an axis.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- OpenStax College, College Physics. September 18, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42182/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Provided by: Light and Matter. Located at: http://lightandmatter.com/simplee.pdf. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/angular-momentum. License: CC BY-SA: Attribution-ShareAlike
- torque. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/torque. License: CC BY-SA: Attribution-ShareAlike
- quantum mechanics. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/quantum_mechanics. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 9, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42182/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Conservation of Angular Momentum Theory. Located at: http://www.youtube.com/watch?v=k9IFb3g2e2M. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42182/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Provided by: Light and Matter. Located at: http://lightandmatter.com/meh.pdf. License: CC BY: Attribution
- rotation. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/rotation. License: CC BY-SA: Attribution-ShareAlike
- momentum. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/momentum. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. November 9, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42182/latest/?collection=col11406/1.7. License: CC BY: Attribution
- Conservation of Angular Momentum Theory. Located at: http://www.youtube.com/watch?v=k9IFb3g2e2M. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/514cc462b483dab00d000947/arrow.jpg. License: CC BY: Attribution
- Ball. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Ball. License: Public Domain: No Known Copyright


