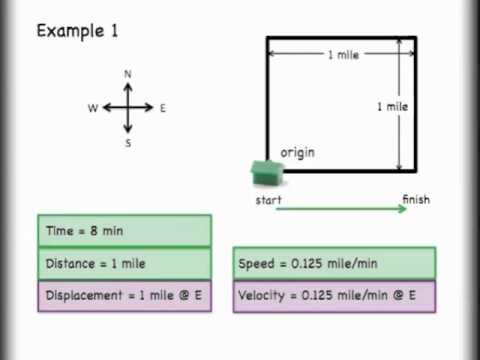
5.10: Vectors Revisited
- Last updated
- Jun 17, 2019
- Save as PDF
- Page ID
- 18144

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Components of a Vector
Vectors are geometric representations of magnitude and direction and can be expressed as arrows in two or three dimensions.
learning objectives
- Contrast two-dimensional and three-dimensional vectors
Vectors are geometric representations of magnitude and direction which are often represented by straight arrows, starting at one point on a coordinate axis and ending at a different point. All vectors have a length, called the magnitude, which represents some quality of interest so that the vector may be compared to another vector. Vectors, being arrows, also have a direction. This differentiates them from scalars, which are mere numbers without a direction.
A vector is defined by its magnitude and its orientation with respect to a set of coordinates. It is often useful in analyzing vectors to break them into their component parts. For two-dimensional vectors, these components are horizontal and vertical. For three dimensional vectors, the magnitude component is the same, but the direction component is expressed in terms of xx, yy and zz.
Decomposing a Vector
To visualize the process of decomposing a vector into its components, begin by drawing the vector from the origin of a set of coordinates. Next, draw a straight line from the origin along the x-axis until the line is even with the tip of the original vector. This is the horizontal component of the vector. To find the vertical component, draw a line straight up from the end of the horizontal vector until you reach the tip of the original vector. You should find you have a right triangle such that the original vector is the hypotenuse.
Decomposing a vector into horizontal and vertical components is a very useful technique in understanding physics problems. Whenever you see motion at an angle, you should think of it as moving horizontally and vertically at the same time. Simplifying vectors in this way can speed calculations and help to keep track of the motion of objects.
Scalars and Vectors: Mr. Andersen explains the differences between scalar and vectors quantities. He also uses a demonstration to show the importance of vectors and vector addition.
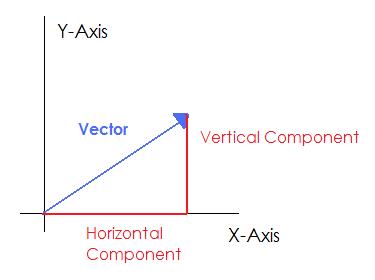
Components of a Vector: The original vector, defined relative to a set of axes. The horizontal component stretches from the start of the vector to its furthest x-coordinate. The vertical component stretches from the x-axis to the most vertical point on the vector. Together, the two components and the vector form a right triangle.
Scalars vs. Vectors
Scalars are physical quantities represented by a single number, and vectors are represented by both a number and a direction.
learning objectives
- Distinguish the difference between the quantities scalars and vectors represent
Physical quantities can usually be placed into two categories, vectors and scalars. These two categories are typified by what information they require. Vectors require two pieces of information: the magnitude and direction. In contrast, scalars require only the magnitude. Scalars can be thought of as numbers, whereas vectors must be thought of more like arrows pointing in a specific direction.

A Vector: An example of a vector. Vectors are usually represented by arrows with their length representing the magnitude and their direction represented by the direction the arrow points.
Vectors require both a magnitude and a direction. The magnitude of a vector is a number for comparing one vector to another. In the geometric interpretation of a vector the vector is represented by an arrow. The arrow has two parts that define it. The two parts are its length which represents the magnitude and its direction with respect to some set of coordinate axes. The greater the magnitude, the longer the arrow. Physical concepts such as displacement, velocity, and acceleration are all examples of quantities that can be represented by vectors. Each of these quantities has both a magnitude (how far or how fast) and a direction. In order to specify a direction, there must be something to which the direction is relative. Typically this reference point is a set of coordinate axes like the x-y plane.
Scalars differ from vectors in that they do not have a direction. Scalars are used primarily to represent physical quantities for which a direction does not make sense. Some examples of these are: mass, height, length, volume, and area. Talking about the direction of these quantities has no meaning and so they cannot be expressed as vectors.
The difference between Vectors and Scalars, Introduction and Basics: This video introduces the difference between scalars and vectors. Ideas about magnitude and direction are introduced and examples of both vectors and scalars are given.
Adding and Subtracting Vectors Graphically
Vectors may be added or subtracted graphically by laying them end to end on a set of axes.
learning objectives
- Distinguish the difference between the quantities scalars and vectors represent
Adding and Subtracting Vectors
One of the ways in which representing physical quantities as vectors makes analysis easier is the ease with which vectors may be added to one another. Since vectors are graphical visualizations, addition and subtraction of vectors can be done graphically.
The graphical method of vector addition is also known as the head-to-tail method. To start, draw a set of coordinate axes. Next, draw out the first vector with its tail (base) at the origin of the coordinate axes. For vector addition it does not matter which vector you draw first since addition is commutative, but for subtraction ensure that the vector you draw first is the one you are subtracting from. The next step is to take the next vector and draw it such that its tail starts at the previous vector’s head (the arrow side). Continue to place each vector at the head of the preceding one until all the vectors you wish to add are joined together. Finally, draw a straight line from the origin to the head of the final vector in the chain. This new line is the vector result of adding those vectors together.
Graphical Addition of Vectors: The head-to-tail method of vector addition requires that you lay out the first vector along a set of coordinate axes. Next, place the tail of the next vector on the head of the first one. Draw a new vector from the origin to the head of the last vector. This new vector is the sum of the original two.
Vector Addition Lesson 1 of 2: Head to Tail Addition Method: This video gets viewers started with vector addition and subtraction. The first lesson shows graphical addition while the second video takes a more mathematical approach and shows vector addition by components.
To subtract vectors the method is similar. Make sure that the first vector you draw is the one to be subtracted from. Then, to subtract a vector, proceed as if adding the opposite of that vector. In other words, flip the vector to be subtracted across the axes and then join it tail to head as if adding. To flip the vector, simply put its head where its tail was and its tail where its head was.
Adding and Subtracting Vectors Using Components
It is often simpler to add or subtract vectors by using their components.
learning objectives
- Demonstrate how to add and subtract vectors by components
Using Components to Add and Subtract Vectors
Another way of adding vectors is to add the components. Previously, we saw that vectors can be expressed in terms of their horizontal and vertical components. To add vectors, merely express both of them in terms of their horizontal and vertical components and then add the components together.
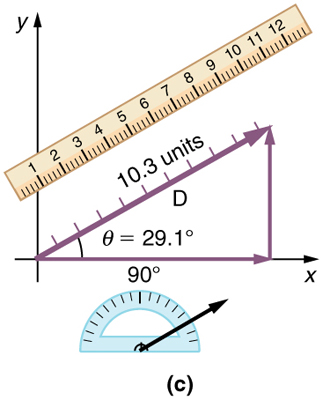
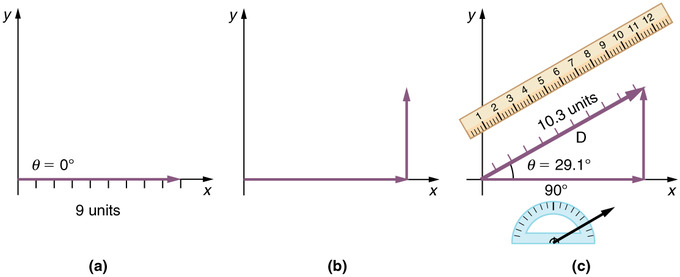
Vector with Horizontal and Vertical Components: The vector in this image has a magnitude of 10.3 units and a direction of 29.1 degrees above the x-axis. It can be decomposed into a horizontal part and a vertical part as shown.
For example, a vector with a length of 5 at a 36.9 degree angle to the horizontal axis will have a horizontal component of 4 units and a vertical component of 3 units. If we were to add this to another vector of the same magnitude and direction, we would get a vector twice as long at the same angle. This can be seen by adding the horizontal components of the two vectors (4+4) and the two vertical components (3+3). These additions give a new vector with a horizontal component of 8(4+4) and a vertical component of 6(3+3). To find the resultant vector, simply place the tail of the vertical component at the head (arrow side) of the horizontal component and then draw a line from the origin to the head of the vertical component. This new line is the resultant vector. It should be twice as long as the original, since both of its components are twice as large as they were previously.
To subtract vectors by components, simply subtract the two horizontal components from each other and do the same for the vertical components. Then draw the resultant vector as you did in the previous part.
Vector Addition Lesson 2 of 2: How to Add Vectors by Components: This video gets viewers started with vector addition using a mathematical approach and shows vector addition by components.
Multiplying Vectors by a Scalar
Multiplying a vector by a scalar changes the magnitude of the vector but not the direction.
learning objectives
- Summarize the interaction between vectors and scalars
Overview
Although vectors and scalars represent different types of physical quantities, it is sometimes necessary for them to interact. While adding a scalar to a vector is impossible because of their different dimensions in space, it is possible to multiply a vector by a scalar. A scalar, however, cannot be multiplied by a vector.
To multiply a vector by a scalar, simply multiply the similar components, that is, the vector’s magnitude by the scalar’s magnitude. This will result in a new vector with the same direction but the product of the two magnitudes.
Example 5.10.1:
For example, if you have a vector A with a certain magnitude and direction, multiplying it by a scalar a with magnitude 0.5 will give a new vector with a magnitude of half the original. Similarly if you take the number 3 which is a pure and unit-less scalar and multiply it to a vector, you get a version of the original vector which is 3 times as long. As a more physical example take the gravitational force on an object. The force is a vector with its magnitude depending on the scalar known as mass and its direction being down. If the mass of the object is doubled, the force of gravity is doubled as well.
Multiplying vectors by scalars is very useful in physics. Most of the units used in vector quantities are intrinsically scalars multiplied by the vector. For example, the unit of meters per second used in velocity, which is a vector, is made up of two scalars, which are magnitudes: the scalar of length in meters and the scalar of time in seconds. In order to make this conversion from magnitudes to velocity, one must multiply the unit vector in a particular direction by these scalars.
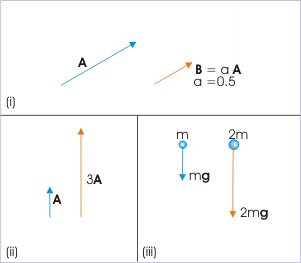
Scalar Multiplication: (i) Multiplying the vector A by the scalar a=0.5 yields the vector B which is half as long. (ii) Multiplying the vector A by 3 triples its length. (iii) Doubling the mass (scalar) doubles the force (vector) of gravity.
Unit Vectors and Multiplication by a Scalar
Multiplying a vector by a scalar is the same as multiplying its magnitude by a number.
learning objectives
- Predict the influence of multiplying a vector by a scalar
In addition to adding vectors, vectors can also be multiplied by constants known as scalars. Scalars are distinct from vectors in that they are represented by a magnitude but no direction. Examples of scalars include an object’s mass, height, or volume.
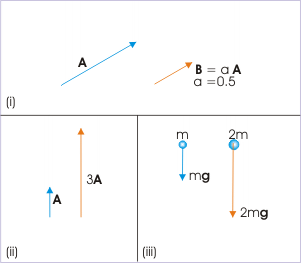
Scalar Multiplication: (i) Multiplying the vector A by the scalar a=0.5 yields the vector B which is half as long. (ii) Multiplying the vector A by 3 triples its length. (iii) Doubling the mass (scalar) doubles the force (vector) of gravity.
When multiplying a vector by a scalar, the direction of the vector is unchanged and the magnitude is multiplied by the magnitude of the scalar. This results in a new vector arrow pointing in the same direction as the old one but with a longer or shorter length. You can also accomplish scalar multiplication through the use of a vector’s components. Once you have the vector’s components, multiply each of the components by the scalar to get the new components and thus the new vector.
A useful concept in the study of vectors and geometry is the concept of a unit vector. A unit vector is a vector with a length or magnitude of one. The unit vectors are different for different coordinates. In Cartesian coordinates the directions are x and y usually denoted ˆx and ˆy. With the triangle above the letters referred to as a “hat”. The unit vectors in Cartesian coordinates describe a circle known as the “unit circle” which has radius one. This can be seen by taking all the possible vectors of length one at all the possible angles in this coordinate system and placing them on the coordinates. If you were to draw a line around connecting all the heads of all the vectors together, you would get a circle of radius one.
Position, Displacement, Velocity, and Acceleration as Vectors
Position, displacement, velocity, and acceleration can all be shown vectors since they are defined in terms of a magnitude and a direction.
learning objectives
- Examine the applications of vectors in analyzing physical quantities
Use of Vectors
Vectors can be used to represent physical quantities. Most commonly in physics, vectors are used to represent displacement, velocity, and acceleration. Vectors are a combination of magnitude and direction, and are drawn as arrows. The length represents the magnitude and the direction of that quantity is the direction in which the vector is pointing. Because vectors are constructed this way, it is helpful to analyze physical quantities (with both size and direction) as vectors.
Applications
In physics, vectors are useful because they can visually represent position, displacement, velocity and acceleration. When drawing vectors, you often do not have enough space to draw them to the scale they are representing, so it is important to denote somewhere what scale they are being drawn at. For example, when drawing a vector that represents a magnitude of 100, one may draw a line that is 5 units long at a scale of 120. When the inverse of the scale is multiplied by the drawn magnitude, it should equal the actual magnitude.
Position and Displacement
Displacement is defined as the distance, in any direction, of an object relative to the position of another object. Physicists use the concept of a position vector as a graphical tool to visualize displacements. A position vector expresses the position of an object from the origin of a coordinate system. A position vector can also be used to show the position of an object in relation to a reference point, secondary object or initial position (if analyzing how far the object has moved from its original location). The position vector is a straight line drawn from the arbitrary origin to the object. Once drawn, the vector has a length and a direction relative to the coordinate system used.
Velocity
Velocity is also defined in terms of a magnitude and direction. To say that something is gaining or losing velocity one must also say how much and in what direction. For example, an airplane flying at 200 kmh to the northeast can be represented by an vector pointing in the northeast direction with a magnitude of 200 kmh . In drawing the vector, the magnitude is only important as a way to compare two vectors of the same units. So, if there were another airplane flying 100 kmh to the southwest, the vector arrow should be half as long and pointing in the direction of southwest.
Acceleration
Acceleration, being the time rate of change of velocity, is composed of a magnitude and a direction, and is drawn with the same concept as a velocity vector. A value for acceleration would not be helpful in physics if the magnitude and direction of this acceleration was unknown, which is why these vectors are important. In a free body diagram, for example, of an object falling, it would be helpful to use an acceleration vector near the object to denote its acceleration towards the ground. If gravity is the only force acting on the object, this vector would be pointing downward with a magnitude of 9.81 ms2 of 32.2 fts2.

Vector Diagram: Here is a man walking up a hill. His direction of travel is defined by the angle theta relative to the vertical axis and by the length of the arrow going up the hill. He is also being accelerated downward by gravity.
Key Points
- Vectors can be broken down into two components: magnitude and direction.
- By taking the vector to be analyzed as the hypotenuse, the horizontal and vertical components can be found by completing a right triangle. The bottom edge of the triangle is the horizontal component and the side opposite the angle is the vertical component.
- The angle that the vector makes with the horizontal can be used to calculate the length of the two components.
- Scalars are physical quantities represented by a single number and no direction.
- Vectors are physical quantities that require both magnitude and direction.
- Examples of scalars include height, mass, area, and volume. Examples of vectors include displacement, velocity, and acceleration.
- To add vectors, lay the first one on a set of axes with its tail at the origin. Place the next vector with its tail at the previous vector’s head. When there are no more vectors, draw a straight line from the origin to the head of the last vector. This line is the sum of the vectors.
- To subtract vectors, proceed as if adding the two vectors, but flip the vector to be subtracted across the axes and then join it tail to head as if adding.
- Adding or subtracting any number of vectors yields a resultant vector.
- Vectors can be decomposed into horizontal and vertical components.
- Once the vectors are decomposed into components, the components can be added.
- Adding the respective components of two vectors yields a vector which is the sum of the two vectors.
- A vector is a quantity with both magnitude and direction.
- A scalar is a quantity with only magnitude.
- Multiplying a vector by a scalar is equivalent to multiplying the vector’s magnitude by the scalar. The vector lengthens or shrinks but does not change direction.
- A unit vector is a vector of magnitude ( length ) 1.
- A scalar is a physical quantity that can be represented by a single number. Unlike vectors, scalars do not have direction.
- Multiplying a vector by a scalar is the same as multiplying the vector’s magnitude by the number represented by the scalar.
- Vectors are arrows consisting of a magnitude and a direction. They are used in physics to represent physical quantities that also have both magnitude and direction.
- Displacement is a physics term meaning the distance of an object from a reference point. Since the displacement contains two pieces of information: the distance from the reference point and the direction away from the point, it is well represented by a vector.
- Velocity is defined as the rate of change in time of the displacement. To know the velocity of an object one must know both how fast the displacement is changing and in what direction. Therefore it is also well represented by a vector.
- Acceleration, being the rate of change of velocity also requires both a magnitude and a direction relative to some coordinates.
- When drawing vectors, you often do not have enough space to draw them to the scale they are representing, so it is important to denote somewhere what scale they are being drawn at.
Key Terms
- coordinates: Numbers indicating a position with respect to some axis. Ex: x and y coordinates indicate position relative to xx and yy axes.
- axis: An imaginary line around which an object spins or is symmetrically arranged.
- magnitude: A number assigned to a vector indicating its length.
- Coordinate axes: A set of perpendicular lines which define coordinates relative to an origin. Example: x and y coordinate axes define horizontal and vertical position.
- origin: The center of a coordinate axis, defined as being the coordinate 0 in all axes.
- Component: A part of a vector. For example, horizontal and vertical components.
- vector: A directed quantity, one with both magnitude and direction; the between two points.
- magnitude: A number assigned to a vector indicating its length.
- scalar: A quantity that has magnitude but not direction; compare vector.
- unit vector: A vector of magnitude 1.
- velocity: The rate of change of displacement with respect to change in time.
- displacement: The length and direction of a straight line between two objects.
- acceleration: the rate at which the velocity of a body changes with time
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Sunil Kumar Singh, Components of a Vector. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14519/latest/. License: CC BY: Attribution
- Euclidean vector. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Euclidean_vector. License: CC BY-SA: Attribution-ShareAlike
- axis. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/axis. License: CC BY-SA: Attribution-ShareAlike
- coordinates. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/coordinates. License: CC BY-SA: Attribution-ShareAlike
- magnitude. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/magnitude. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Scalar (physics). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Scalar_(physics). License: CC BY-SA: Attribution-ShareAlike
- Euclidean vector. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Euclidean_vector. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/coordinate-axes. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/coordinate-axes. License: CC BY-SA: Attribution-ShareAlike
- origin. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/origin. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_03.jpg. License: CC BY: Attribution
- Vector Addition Lesson 1 of 2: Head to Tail Addition Method. Located at: http://www.youtube.com/watch?v=7p-uxbu24AM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/. License: CC BY: Attribution
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/component. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_03.jpg. License: CC BY: Attribution
- Vector Addition Lesson 1 of 2: Head to Tail Addition Method. Located at: http://www.youtube.com/watch?v=7p-uxbu24AM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_06a.jpg. License: CC BY: Attribution
- Vector Addition Lesson 2 of 2: How to Add Vectors by Components. Located at: http://www.youtube.com/watch?v=tvrynGECJ7k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Scalar (Dot) Product. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/. License: CC BY: Attribution
- scalar. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/scalar. License: CC BY-SA: Attribution-ShareAlike
- vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/vector. License: CC BY-SA: Attribution-ShareAlike
- magnitude. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/magnitude. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_03.jpg. License: CC BY: Attribution
- Vector Addition Lesson 1 of 2: Head to Tail Addition Method. Located at: http://www.youtube.com/watch?v=7p-uxbu24AM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_06a.jpg. License: CC BY: Attribution
- Vector Addition Lesson 2 of 2: How to Add Vectors by Components. Located at: http://www.youtube.com/watch?v=tvrynGECJ7k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Scalar (Dot) Product. March 12, 2014. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/vm2a.gif. License: CC BY: Attribution
- Unit vector. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Unit_vector. License: CC BY-SA: Attribution-ShareAlike
- Scalar (physics). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Scalar_(physics). License: CC BY-SA: Attribution-ShareAlike
- Sunil Kumar Singh, Scalar (Dot) Product. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/. License: CC BY: Attribution
- scalar. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/scalar. License: CC BY-SA: Attribution-ShareAlike
- unit vector. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/unit_vector. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_03.jpg. License: CC BY: Attribution
- Vector Addition Lesson 1 of 2: Head to Tail Addition Method. Located at: http://www.youtube.com/watch?v=7p-uxbu24AM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_06a.jpg. License: CC BY: Attribution
- Vector Addition Lesson 2 of 2: How to Add Vectors by Components. Located at: http://www.youtube.com/watch?v=tvrynGECJ7k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Scalar (Dot) Product. March 12, 2014. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/vm2a.gif. License: CC BY: Attribution
- Sunil Kumar Singh, Scalar (Dot) Product. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/vm2a.gif. License: CC BY: Attribution
- Displacement (vector). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Displacement_(vector). License: CC BY-SA: Attribution-ShareAlike
- displacement. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/displacement. License: CC BY-SA: Attribution-ShareAlike
- acceleration. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/acceleration. License: CC BY-SA: Attribution-ShareAlike
- velocity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/velocity. License: CC BY-SA: Attribution-ShareAlike
- Scalars and Vectors. Located at: http://www.youtube.com/watch?v=EUrMI0DIh40. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5101a2b3e4b04253d8aba44b/vectordecomp.jpg. License: CC BY: Attribution
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5d/Position_vector.svg/220px-Position_vector.svg.png. License: CC BY: Attribution
- The difference between Vectors and Scalars, Introduction and Basics. Located at: http://www.youtube.com/watch?v=bap6XjDDE3k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_03.jpg. License: CC BY: Attribution
- Vector Addition Lesson 1 of 2: Head to Tail Addition Method. Located at: http://www.youtube.com/watch?v=7p-uxbu24AM. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- OpenStax College, Vector Addition and Subtraction: Graphical Methods. January 24, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42127/latest/Figure_03_02_06a.jpg. License: CC BY: Attribution
- Vector Addition Lesson 2 of 2: How to Add Vectors by Components. Located at: http://www.youtube.com/watch?v=tvrynGECJ7k. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Sunil Kumar Singh, Scalar (Dot) Product. March 12, 2014. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/vm2a.gif. License: CC BY: Attribution
- Sunil Kumar Singh, Scalar (Dot) Product. January 16, 2015. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m14513/latest/vm2a.gif. License: CC BY: Attribution
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/510a0e5de4b0f11e4bcb01ad/Man_walking_up_a_hill.png. License: CC BY: Attribution