13.4: Methods of Heat Transfer

learning objectives

• Assess why particular characteristics are necessary for effective conduction

Conduction

Conduction is the transfer of heat through stationary matter by physical contact. (The matter is stationary on a macroscopic scale—we know there is thermal motion of the atoms and molecules at any temperature above absolute zero.) Heat transferred from an electric stove to the bottom of a pot is an example of conduction.

Some materials conduct thermal energy faster than others. For example, the pillow in your room may the same temperature as the metal doorknob, but the doorknob feels cooler to the touch. In general, good conductors of electricity (metals like copper, aluminum, gold, and silver) are also good heat conductors, whereas insulators of electricity (wood, plastic, and rubber) are poor heat conductors.

Microscopic Description of Conduction

On a microscopic scale, conduction occurs as rapidly moving or vibrating atoms and molecules interact with neighboring particles, transferring some of their kinetic energy. Heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in thermal contact. Conduction is greater in solids because the network of relatively close fixed spatial relationships between atoms helps to transfer energy between them by vibration.

Fluids and gases are less conductive than solids. This is due to the large distance between atoms in a fluid or (especially) a gas: fewer collisions between atoms means less conduction.

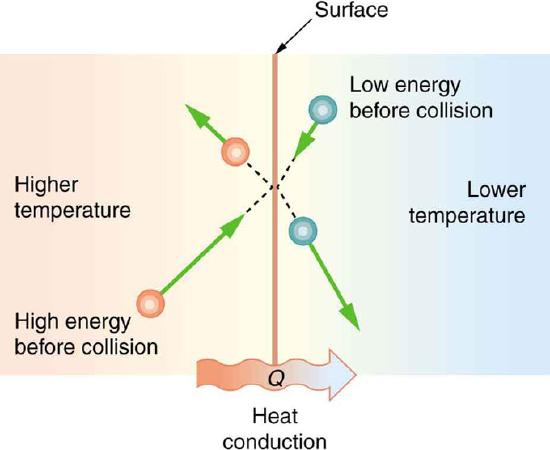
Microscopic Illustration of Conduction: The molecules in two bodies at different temperatures have different average kinetic energies. Collisions occurring at the contact surface tend to transfer energy from high-temperature regions to low-temperature regions. In this illustration, a molecule in the lower temperature region (right side) has low energy before collision, but its energy increases after colliding with the contact surface. In contrast, a molecule in the higher temperature region (left side) has high energy before collision, but its energy decreases after colliding with the contact surface.

The (average) kinetic energy of a molecule in the hot body is higher than in the colder body. If two molecules collide, an energy transfer from the hot to the cold molecule occurs (see the above figure). The cumulative effect from all collisions results in a net flux of heat from the hot body to the colder body. The heat flux thus depends on the temperature difference \(\mathrm{T=T_{hot}−T_{cold}}\). Therefore, you will get a more severe burn from boiling water than from hot tap water. Conversely, if the temperatures are the same, the net heat transfer rate falls to zero, and equilibrium is achieved. Owing to the fact that the number of collisions increases with increasing area, heat conduction depends on the cross-sectional area. If you touch a cold wall with your palm, your hand cools faster than if you just touch it with your fingertip.

Factors Affecting the Rate of Heat Transfer Through Conduction

In addition to temperature and cross-sectional area, another factor affecting conduction is the thickness of the material through which the heat transfers. Heat transfer from the left side to the right side is accomplished by a series of molecular collisions. The thicker the material, the more time it takes to transfer the same amount of heat. If you get cold during the night, you may retrieve a thicker blanket to keep warm.

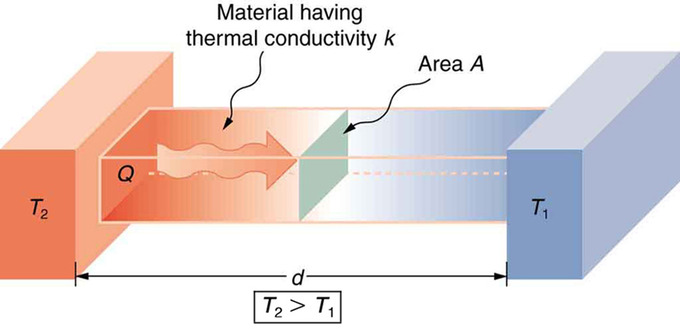
Effect of Thickness on Heat Conduction: Heat conduction occurs through any material, represented here by a rectangular bar. The temperature of the material is \(\mathrm{T_2}\) on the left and \(\mathrm{T_1}\) on the right, where \(\mathrm{T_2}\) is greater than \(\mathrm{T_1}\). The rate of heat transfer by conduction is directly proportional to the surface area \(\mathrm{A}\), the temperature difference \(\mathrm{T_2−T_1}\), and the substance’s conductivity kk. The rate of heat transfer is inversely proportional to the thickness \(\mathrm{d}\).

Lastly, the heat transfer rate depends on the material properties described by the coefficient of thermal conductivity. All four factors are included in a simple equation that was deduced from and is confirmed by experiments. The rate of conductive heat transfer through a slab of material, such as the one in the figure above is given by \(\mathrm{\frac{Q}{t}=\frac{kA(T_2−T_1)}{d}}\) where \(\mathrm{\frac{Q}{t}}\) is the rate of heat transfer in Joules per second (Watts), \(\mathrm{k}\) is the thermal conductivity of the material, \(\mathrm{A}\) and \(\mathrm{d}\) are its surface area and thickness, and \(\mathrm{(T_2−T_1)}\) is the temperature difference across the slab.

Convection

Convection is the heat transfer by the macroscopic movement of a fluid, such as a car’s engine kept cool by the water in the cooling system.

learning objectives

• Illustrate the mechanisms of convection with phase change

Example \(\PageIndex{1}\):

Calculating Heat Transfer by Convection: Convection of Air Through the Walls of a House.

Most houses are not airtight: air goes in and out around doors and windows, through cracks and crevices, following wiring to switches and outlets, and so on. The air in a typical house is completely replaced in less than an hour.

Suppose that a moderately-sized house has inside dimensions 12.0 m × 18.0 m × 3.00 m high, and that all air is replaced in 30.0 min. Calculate the heat transfer per unit time in watts needed to warm the incoming cold air by 10.0 ºC, thus replacing the heat transferred by convection alone.

Strategy:

Heat is used to raise the temperature of air so that \(\mathrm{Q=mcΔT}\). The rate of heat transfer is then \(\mathrm{\frac{Q}{t}}\), where \(\mathrm{t}\) is the time for air turnover. We are given that \(\mathrm{ΔT}\) is 10.0ºC, but we must still find values for the mass of air and its specific heat before we can calculate QQ. The specific heat of air is a weighted average of the specific heats of nitrogen and oxygen, which is \(\mathrm{c=cp≅1000 \;J/kg⋅C}\) (note that the specific heat at constant pressure must be used for this process).

Solution

(1) Determine the mass of air from its density and the given volume of the house. The density is given from the density \(\mathrm{ρ}\) and the volume \(\mathrm{m=ρV=(1.29 \; kg/m3)(12.0 \; m \times 18.0 \; m \times 3.00 \; m)=836 \; kg}\)

(2) Calculate the heat transferred from the change in air temperature: \(\mathrm{Q=mcΔT}\) so that \(\mathrm{Q=(836 \; kg)( 1000 \; J/kg⋅∘C)(10∘C)=8.36×10^6 \; J}\)

(3) Calculate the heat transfer from the heat \(\mathrm{Q}\) and the turnover time \(\mathrm{t}\). Since air is turned over in \(\mathrm{t=0.500 \; h=1800 \; s}\), the heat transferred per unit time is \(\mathrm{\frac{Q}{t}=\frac{8.36 \times 10^6 \;J }{1800 \; s}=4.64 \; kW}\).

This rate of heat transfer is equal to the power consumed by about forty-six 100-W light bulbs.

Newly constructed homes are designed for a turnover time of 2 hours or more, rather than 30 minutes for the house of this example. Weather stripping, caulking, and improved window seals are commonly employed. More extreme measures are sometimes taken in very cold (or hot) climates to achieve a tight standard of more than 6 hours for one air turnover. Still longer turnover times are unhealthy, because a minimum amount of fresh air is necessary to supply oxygen for breathing and to dilute household pollutants. The term used for the process by which outside air leaks into the house from cracks around windows, doors, and the foundation is called “air infiltration.”

Convection

Convection (illustrated in ) is the concerted, collective movement of ensembles of molecules within fluids (e.g., liquids, gases). Convection of mass cannot take place in solids, since neither bulk current flows nor significant diffusion can occur in solids. Instead heat diffusion in solids is called heat conduction, which we’ve just reviewed.

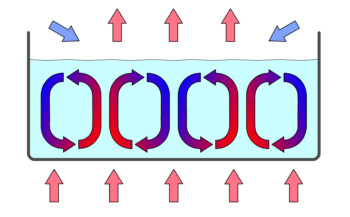
Convection Cells: Convection cells in a gravity field.

Convection is driven by large-scale flow of matter. In the case of Earth, the atmospheric circulation is caused by the flow of hot air from the tropics to the poles, and the flow of cold air from the poles toward the tropics. (Note that Earth’s rotation causes changes in the direction of airflow depending on latitude.). An example of convection is a car engine kept cool by the flow of water in the cooling system, with the water pump maintaining a flow of cool water to the pistons.

While convection is usually more complicated than conduction, we can describe convection and perform some straightforward, realistic calculations of its effects. Natural convection is driven by buoyant forces: hot air rises because density decreases as temperature increases. This principle applies equally with any fluid. For example, the pot of water on the stove in is kept warm in this manner; ocean currents and large-scale atmospheric circulation transfer energy from one part of the globe to another.

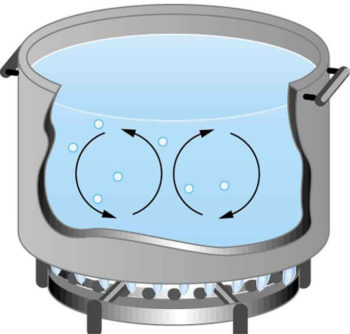
Convection in a Pot of Water: Convection plays an important role in heat transfer inside this pot of water. Once conducted to the inside, heat transfer to other parts of the pot is mostly by convection. The hotter water expands, decreases in density, and rises to transfer heat to other regions of the water, while colder water sinks to the bottom. This process keeps repeating.

Convection and Insulation

Although air can transfer heat rapidly by convection, it is a poor conductor and thus a good insulator. The amount of available space for airflow determines whether air acts as an insulator or conductor. The space between the inside and outside walls of a house, for example, is about 9 cm (3.5 in)—large enough for convection to work effectively. The addition of wall insulation prevents airflow, so heat loss (or gain) is decreased. Similarly, the gap between the two panes of a double-paned window is about 1 cm, which prevents convection and takes advantage of air’s low conductivity to prevent greater loss. Fur, fiber and fiberglass also take advantage of the low conductivity of air by trapping it in spaces too small to support convection. In animals, fur and feathers are lightweight and thus ideal for their protection.

Convection and Phase Changes

Some interesting phenomena happen when convection is accompanied by a phase change. It allows us to cool off by sweating, even if the temperature of the surrounding air exceeds body temperature. Heat from the skin is required in order for sweat to evaporate from the skin, but without air flow the air becomes saturated and evaporation stops. Air flow caused by convection replaces the saturated air by dry air and thus evaporation continues.

Another important example of the combination of phase change and convection occurs when water evaporates from the ocean. Heat is removed from the ocean when water evaporates. If the water vapor condenses in liquid droplets as clouds form, heat is released in the atmosphere (this heat release is latent heat) . Thus, an overall transfer of heat from the ocean to the atmosphere occurs. This process is the driving power behind thunderheads—great cumulus clouds that rise as much as 20.0 km into the stratosphere. Water vapor carried in by convection condenses, releasing tremendous amounts of energy, and this energy allows air to become more buoyant (warmer than its surroundings) and rise. As the air continues to rise, more condensation occurs, which in turn drives the cloud even higher. Such a mechanism is called positive feedback, since the process reinforces and accelerates itself. These systems sometimes produce violent storms with lightning and hail, and constitute the mechanism that drives hurricanes.

Cumulus Clouds: Cumulus clouds are caused by water vapor that rises because of convection. The rise of clouds is driven by a positive feedback mechanism.

Radiation

Radiation is the transfer of heat through electromagnetic energy

learning objectives

• Explain how the energy of electromagnetic radiation corresponds with wavelength

Radiation

You can feel heat transfer from a fire or the Sun. Yet the space between Earth and the Sun is largely empty, without any possibility of heat transfer by convection or conduction. Similarly, you can tell that an oven is hot without touching it or looking inside—it just warms you as you walk by.

In these examples, heat is transferred by radiation. The hot body emits electromagnetic waves that are absorbed by our skin, and no medium is required for them to propagate. We use different names for electromagnetic waves of different wavelengths: radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays .

Radiation from a Fire: Most of the heat transfer from this fire to the observers is through infrared radiation. The visible light, although dramatic, transfers relatively little thermal energy. Convection transfers energy away from the observers as hot air rises, while conduction is negligibly slow here. Skin is very sensitive to infrared radiation so that you can sense the presence of a fire without looking at it directly.

The energy of electromagnetic radiation depends on its wavelength (color) and varies over a wide range; a smaller wavelength (or higher frequency) corresponds to a higher energy. We can write this as:

\[\mathrm{E=hf=\dfrac{hc}{λ}}\]

where \(\mathrm{E}\) is the energy, \(\mathrm{f}\) is the frequency, \(\mathrm{λ}\) is the wavelength, and \(\mathrm{h}\) is a constant.

Because more heat is radiated at higher temperatures, a temperature change is accompanied by a color change. For example, an electrical element on a stove glows from red to orange, while the higher-temperature steel in a blast furnace glows from yellow to white. The radiation you feel is mostly infrared, which is lower in temperature still.

The radiated energy depends on its intensity, which is represented by the height of the distribution .

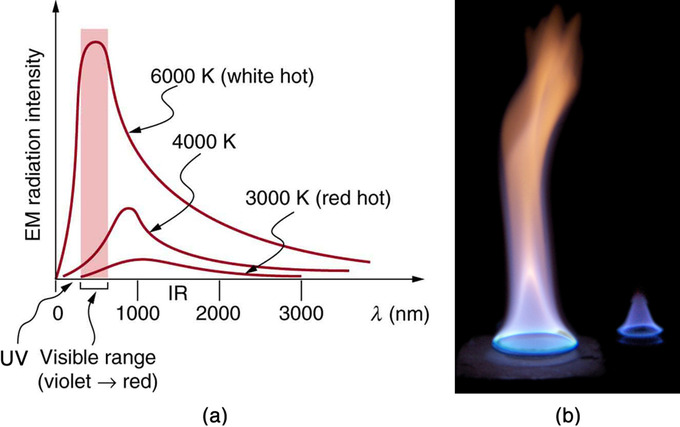
Radiation Spectrum: (a) A graph of the spectra of electromagnetic waves emitted from an ideal radiator at three different temperatures. The intensity or rate of radiation emission increases dramatically with temperature, and the spectrum shifts toward the visible and ultraviolet parts of the spectrum. The shaded portion denotes the visible part of the spectrum. It is apparent that the shift toward the ultraviolet with temperature makes the visible appearance shift from red to white to blue as temperature increases. (b) Note the variations in color corresponding to variations in flame temperature.

Heat Transfer

All objects absorb and emit electromagnetic radiation. The rate of heat transfer by radiation is largely determined by the color of the object. Black is the most effective, and white the least. People living in hot climates generally avoid wearing black clothing, for instance. Similarly, black asphalt in a parking lot will be hotter than the adjacent gray sidewalk on a summer day, because black absorbs better than gray. The reverse is also true—black radiates better than gray. Thus, on a clear summer night the asphalt will be colder than the gray sidewalk because black radiates energy more rapidly than gray.

An ideal radiator, often called a blackbody, is the same color as an ideal absorber, and captures all the radiation that falls on it. In contrast, white is a poor absorber and also a poor radiator. A white object reflects all radiation, like a mirror. (A perfect, polished white surface is mirror-like in appearance, and a crushed mirror looks white. )

There is a clever relation between the temperature of an ideal radiator and the wavelength at which it emits the most radiation. It is called Wien’s displacement law and is given by:

\[\mathrm{λ_maxT=b}\]

where \(\mathrm{b}\) is a constant equal to \(\mathrm{2.9 \times 10^{−3} \; m⋅K}\).

Gray objects have a uniform ability to absorb all parts of the electromagnetic spectrum. Colored objects behave in similar but more complex ways, which gives them a particular color in the visible range and may make them special in other ranges of the nonvisible spectrum. Take, for example, the strong absorption of infrared radiation by the skin, which allows us to be very sensitive to it .

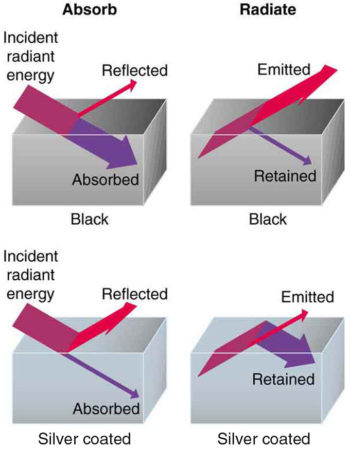
Good and Poor Radiators: A black object is a good absorber and a good radiator, while a white (or silver) object is a poor absorber and a poor radiator. It is as if radiation from the inside is reflected back into the silver object, whereas radiation from the inside of the black object is “absorbed” when it hits the surface and finds itself on the outside and is strongly emitted.

The rate of heat transfer by emitted radiation is determined by the Stefan-Boltzmann law of radiation:

\[\mathrm{\dfrac{Q}{t}=σeAT^4}\]

where \(\mathrm{σ=5.67 \times 10^{−8} \; \frac{J}{s⋅m^2⋅K^4}}\) is the Stefan-Boltzmann constant, A is the surface area of the object, and T is its absolute temperature in kelvin. The symbol e stands for the emissivity of the object, which is a measure of how well it radiates. An ideal jet-black (or blackbody) radiator has e=1e=1, whereas a perfect reflector has \(\mathrm{e=0}\). Real objects fall between these two values. For example, tungsten light bulb filaments have an ee of about 0.5, and carbon black (a material used in printer toner), has the (greatest known) emissivity of about 0.99.

The radiation rate is directly proportional to the fourth power of the absolute temperature—a remarkably strong temperature dependence. Furthermore, the radiated heat is proportional to the surface area of the object. If you knock apart the coals of a fire, there is a noticeable increase in radiation due to an increase in radiating surface area.

Net Rate of Heat Transfer

The net rate of heat transfer by radiation (absorption minus emission) is related to both the temperature of the object and that of its surroundings. Assuming that an object with a temperature \(\mathrm{T_1}\) is surrounded by an environment with uniform temperature \(\mathrm{T_2}\), the net rate of heat transfer by radiation is:

\[\mathrm{\dfrac{Q_{net}}{t}=eAσ(T_2^4−T_1^4)}\)

where e is the emissivity of the object alone. In other words, it does not matter whether the surroundings are white, gray, or black; the balance of radiation into and out of the object depends on how well it emits and absorbs radiation. When \(\mathrm{T_2>T_1}\), the quantity \(\mathrm{\frac{Q_{net}}{t}}\) is positive; that is, the net heat transfer is from hotter objects to colder objects.

Key Points

• On a microscopic scale, conduction occurs as rapidly moving or vibrating atoms and molecules interact with neighboring particles, transferring some of their kinetic energy.
• Conduction is the most significant form of heat transfer within a solid object or between solids in thermal contact.
• Conduction is most significant in solids, and less though in liquids and gases, due to the space between molecules.
• The rate of heat transfer by conduction is dependent on the temperature difference, the size of the area in contact, the thickness of the material, and the thermal properties of the material(s) in contact.
• Convection is driven by the large scale flow of matter in fluids. Solids cannot transport heat through convection.
• Natural convection is driven by buoyant forces: hot air rises because density decreases as temperature increases. This principle applies equally with any fluid.
• Convection can transport heat much more efficiently than conduction. Air is a poor conductor and a good insulator if the space is small enough to prevent convection.
• Convection often accompanies phase changes, such as when sweat evaporates from your body. This mass flow during convection allows humans to cool off even if the surrounding air’s temperature exceeds the body temperature.
• The energy of electromagnetic radiation depends on the wavelength (color) and varies over a wide range: a smaller wavelength (or higher frequency) corresponds to a higher energy.
• All objects emit and absorb electromagnetic energy. The color of an object is related emissivity, or its efficiency of radiating away energy. Black is the most effective while white is the least effective (\(\mathrm{e=1}\) and \(\mathrm{e=0}\), respectively).
• An ideal radiator, often called a blackbody, is the same color as an ideal absorber and captures all the radiation that falls on it.
• The rate of heat transfer by emitted radiation is determined by the Stefan-Boltzmann law of radiation: \(\mathrm{\frac{Q}{t}=σAT^4}\) where \(\mathrm{σ=5.67 \times 10^{−8} \; \frac{J}{s⋅m^2⋅K^4}}\) is the Stefan-Boltzmann constant, \(\mathrm{A}\) is the surface area of the object, and \(\mathrm{T}\) is its absolute temperature in kelvin.
• The net rate of heat transfer is related to the temperature of the object and the temperature of its surroundings. The larger the difference, the higher the net heat flux.
• The temperature of an object is very significant, because the radiation emitted is proportional to this quantity to the fourth power.

Key Terms

• thermal conductivity: the measure of a material’s ability to conduct heat
• natural convection: A method for heat transport. A fluid surrounding a heat source receives heat, becomes less dense and rises. The surrounding, cooler fluid then moves to replace it. This cooler fluid is then heated and the process continues, forming a convection current.
• positive feedback: a feedback loop in which the output of a system is amplified with a net positive gain each cycle.
• blackbody: A theoretical body, approximated by a hole in a hollow black sphere, that absorbs all incident electromagnetic radiation and reflects none; it has a characteristic emission spectrum.
• emissivity: The energy-emitting propensity of a surface, usually measured at a specific wavelength.

LICENSES AND ATTRIBUTIONS

CC LICENSED CONTENT, SHARED PREVIOUSLY

• Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike

CC LICENSED CONTENT, SPECIFIC ATTRIBUTION

• thermal conductivity. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/thermal%20conductivity. License: CC BY-SA: Attribution-ShareAlike
• Conduction (heat). Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Conduction_(heat). License: CC BY-SA: Attribution-ShareAlike
• OpenStax College, College Physics. September 18, 2013. Provided by: OpenStax, CNX. Located at: http://cnx.org/content/m42228/latest/?collection=col11406/1.7. License: CC BY: Attribution
• OpenStax College, College Physics. October 15, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42228/latest/?collection=col11406/1.7. License: CC BY: Attribution
• natural convection. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/natural%20convection. License: CC BY-SA: Attribution-ShareAlike
• Convection. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Convection. License: CC BY-SA: Attribution-ShareAlike
• positive feedback. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/positive_feedback. License: CC BY-SA: Attribution-ShareAlike
• OpenStax College, College Physics. September 17, 2013.. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42229/latest/?collection=col11406/1.7. License: CC BY-SA: Attribution-ShareAlike
• Cumulus Clouds. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Cumulus_clouds. License: CC BY-SA: Attribution-ShareAlike
• blackbody. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/blackbody. License: CC BY-SA: Attribution-ShareAlike
• emissivity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/emissivity. License: CC BY-SA: Attribution-ShareAlike
• OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42230/latest/?collection=col11406/1.7. License: CC BY: Attribution
• Fire. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Fire. License: CC BY-SA: Attribution-ShareAlike