10.2: The Propagation of Light
- Page ID
- 34492
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Determine the index of refraction, given the speed of light in a medium
- List the ways in which light travels from a source to another location
The Speed of Light: Early Measurements
The first measurement of the speed of light was made by the Danish astronomer Ole Roemer (1644–1710) in 1675. He studied the orbit of Io, one of the four large moons of Jupiter, and found that it had a period of revolution of 42.5 h around Jupiter. He also discovered that this value fluctuated by a few seconds, depending on the position of Earth in its orbit around the Sun. Roemer realized that this fluctuation was due to the finite speed of light and could be used to determine c.
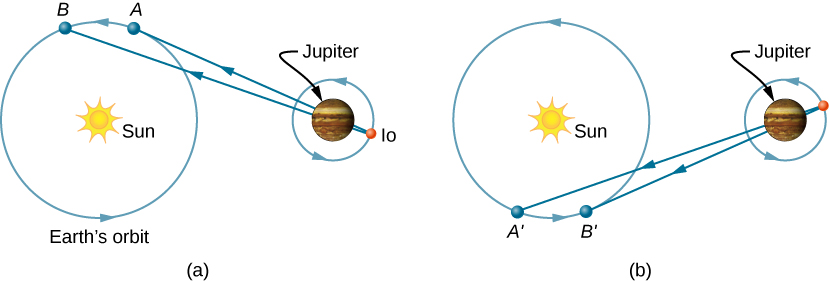
Roemer found the period of revolution of Io by measuring the time interval between successive eclipses by Jupiter. Figure \(\PageIndex{1a}\) shows the planetary configurations when such a measurement is made from Earth in the part of its orbit where it is receding from Jupiter. When Earth is at point A, Earth, Jupiter, and Io are aligned. The next time this alignment occurs, Earth is at point B, and the light carrying that information to Earth must travel to that point. Since B is farther from Jupiter than A, light takes more time to reach Earth when Earth is at B. Now imagine it is about 6 months later, and the planets are arranged as in Figure \(\PageIndex{1b}\). The measurement of Io’s period begins with Earth at point A' and Io eclipsed by Jupiter. The next eclipse then occurs when Earth is at point B', to which the light carrying the information of this eclipse must travel. Since B' is closer to Jupiter than A', light takes less time to reach Earth when it is at B'. This time interval between the successive eclipses of Io seen at A' and B' is therefore less than the time interval between the eclipses seen at A and B. By measuring the difference in these time intervals and with appropriate knowledge of the distance between Jupiter and Earth, Roemer calculated that the speed of light was \(2.0 \times 10^8\,m/s\), which is only 33% below the value accepted today.
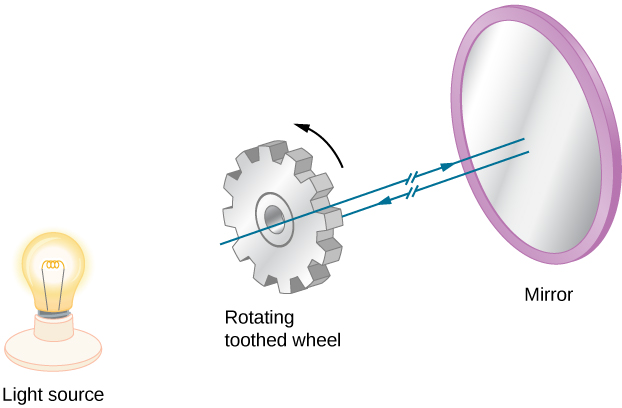
The first successful terrestrial measurement of the speed of light was made by Armand Fizeau (1819–1896) in 1849. He placed a toothed wheel that could be rotated very rapidly on one hilltop and a mirror on a second hilltop 8 km away (Figure \(\PageIndex{2}\)). An intense light source was placed behind the wheel, so that when the wheel rotated, it chopped the light beam into a succession of pulses. The speed of the wheel was then adjusted until no light returned to the observer located behind the wheel. This could only happen if the wheel rotated through an angle corresponding to a displacement of (n+½) teeth, while the pulses traveled down to the mirror and back. Knowing the rotational speed of the wheel, the number of teeth on the wheel, and the distance to the mirror, Fizeau determined the speed of light to be \(3.15 \times 10^8\,m/s\), which is only 5% too high.
The French physicist Jean Bernard Léon Foucault (1819–1868) modified Fizeau’s apparatus by replacing the toothed wheel with a rotating mirror. In 1862, he measured the speed of light to be 2.98×108m/s, which is within 0.6% of the presently accepted value. Albert Michelson (1852–1931) also used Foucault’s method on several occasions to measure the speed of light. His first experiments were performed in 1878; by 1926, he had refined the technique so well that he found c to be (2.99796±4)×108m/s.
Today, the speed of light is known to great precision. In fact, the speed of light in a vacuum c is so important that it is accepted as one of the basic physical quantities and has the value
\[c=2.99792458\times 10^8m/s \equiv 3.00\times 10^8m/s \label{speed} \]
where the approximate value of 3.00×108m/s is used whenever three-digit accuracy is sufficient.
Speed of Light in Matter
The speed of light through matter is less than it is in a vacuum, because light interacts with atoms in a material. The speed of light depends strongly on the type of material, since its interaction varies with different atoms, crystal lattices, and other substructures. We can define a constant of a material that describes the speed of light in it, called the index of refraction n:
\[n=\dfrac{c}{v} \label{index} \]
where \(v\) is the observed speed of light in the material.
Since the speed of light is always less than c in matter and equals c only in a vacuum, the index of refraction is always greater than or equal to one; that is, n≥1. Table \(\PageIndex{1}\) gives the indices of refraction for some representative substances. The values are listed for a particular wavelength of light, because they vary slightly with wavelength. (This can have important effects, such as colors separated by a prism, as we will see in Dispersion.) Note that for gases, n is close to 1.0. This seems reasonable, since atoms in gases are widely separated, and light travels at c in the vacuum between atoms. It is common to take \(n=1\) for gases unless great precision is needed. Although the speed of light v in a medium varies considerably from its value c in a vacuum, it is still a large speed.
Example \(\PageIndex{1}\): Speed of Light in Jewelry
Calculate the speed of light in zircon, a material used in jewelry to imitate diamond.
Strategy
We can calculate the speed of light in a material \(v\) from the index of refraction \(n\) of the material, using Equation \red{index}
Solution
Rearranging Equation \ref{index} for \(v\) gives us
\[v=\dfrac{c}{n}. \nonumber \]
The index of refraction for zircon is given as 1.923 in Table \(\PageIndex{1}\), and \(c\) is given in Equation \ref{speed}. Entering these values in the equation gives
\[\begin{align*} v &=\dfrac{3.00×10^8m/s}{1.923} \\[4pt] &=1.56×10^8m/s. \end{align*} \nonumber \]
Significance
This speed is slightly larger than half the speed of light in a vacuum and is still high compared with speeds we normally experience. The only substance listed in Table \(\PageIndex{1}\) that has a greater index of refraction than zircon is diamond. We shall see later that the large index of refraction for zircon makes it sparkle more than glass, but less than diamond.
Table \(\PageIndex{1}\) shows that ethanol and fresh water have very similar indices of refraction. By what percentage do the speeds of light in these liquids differ?
- Answer
-
2.1% (to two significant figures)
The Ray Model of Light
You have already studied some of the wave characteristics of light in the previous chapter on Electromagnetic Waves. In this chapter, we start mainly with the ray characteristics. There are three ways in which light can travel from a source to another location (Figure \(\PageIndex{1}\)). It can come directly from the source through empty space, such as from the Sun to Earth. Or light can travel through various media, such as air and glass, to the observer. Light can also arrive after being reflected, such as by a mirror. In all of these cases, we can model the path of light as a straight line called a ray.
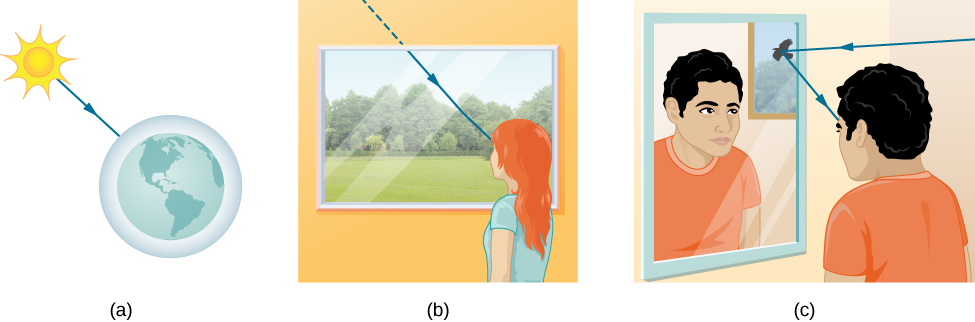
Experiments show that when light interacts with an object several times larger than its wavelength, it travels in straight lines and acts like a ray. Its wave characteristics are not pronounced in such situations. Since the wavelength of visible light is less than a micron (a thousandth of a millimeter), it acts like a ray in the many common situations in which it encounters objects larger than a micron. For example, when visible light encounters anything large enough that we can observe it with unaided eyes, such as a coin, it acts like a ray, with generally negligible wave characteristics.
In all of these cases, we can model the path of light as straight lines. Light may change direction when it encounters objects (such as a mirror) or in passing from one material to another (such as in passing from air to glass), but it then continues in a straight line or as a ray. The word “ray” comes from mathematics and here means a straight line that originates at some point. It is acceptable to visualize light rays as laser rays. The ray model of light describes the path of light as straight lines.
Since light moves in straight lines, changing directions when it interacts with materials, its path is described by geometry and simple trigonometry. This part of optics, where the ray aspect of light dominates, is therefore called geometric optics. Two laws govern how light changes direction when it interacts with matter. These are the law of reflection, for situations in which light bounces off matter, and the law of refraction, for situations in which light passes through matter. We will examine more about each of these laws in upcoming sections of this chapter.