3.1: Motion in Two Dimensions
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 16934

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
Constant Velocity
An object moving with constant velocity must have a constant speed in a constant direction.
learning objectives
- Examine the terms for constant velocity and how they apply to acceleration
Motion with constant velocity is one of the simplest forms of motion. This type of motion occurs when an an object is moving (or sliding) in the presence of little or negligible friction, similar to that of a hockey puck sliding across the ice. To have a constant velocity, an object must have a constant speed in a constant direction. Constant direction constrains the object to motion to a straight path.
Newton’s second law (F=ma) suggests that when a force is applied to an object, the object would experience acceleration. If the acceleration is 0, the object shouldn’t have any external forces applied on it. Mathematically, this can be shown as the following:
a=dvdt=0⇒v=const.
If an object is moving at constant velocity, the graph of distance vs. time (x vs. t) shows the same change in position over each interval of time. Therefore the motion of an object at constant velocity is represented by a straight line: x=x0+vt, where x0 is the displacement when t=0 (or at the y-axis intercept).

Motion with Constant Velocity: When an object is moving with constant velocity, it does not change direction nor speed and therefore is represented as a straight line when graphed as distance over time.
You can also obtain an object’s velocity if you know its trace over time. Given a graph as in, we can calculate the velocity from the change in distance over the change in time. In graphical terms, the velocity can be interpreted as the slope of the line. The velocity can be positive or negative, and is indicated by the sign of our slope. This tells us in which direction the object moves.
Constant Acceleration
Analyzing two-dimensional projectile motion is done by breaking it into two motions: along the horizontal and vertical axes.
learning objectives
- Analyze a two-dimensional projectile motion along horizontal and vertical axes
Projectile motion is the motion of an object thrown, or projected, into the air, subject only to the force of gravity. The object is called a projectile, and its path is called its trajectory. The motion of falling objects is a simple one-dimensional type of projectile motion in which there is no horizontal movement. In two-dimensional projectile motion, such as that of a football or other thrown object, there is both a vertical and a horizontal component to the motion.
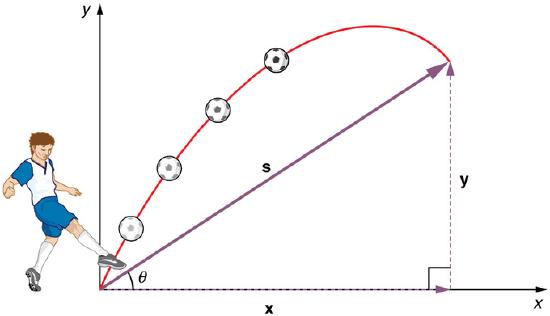
Projectile Motion: Throwing a rock or kicking a ball generally produces a projectile pattern of motion that has both a vertical and a horizontal component.
The most important fact to remember is that motion along perpendicular axes are independent and thus can be analyzed separately. The key to analyzing two-dimensional projectile motion is to break it into two motions, one along the horizontal axis and the other along the vertical. To describe motion we must deal with velocity and acceleration, as well as with displacement.
We will assume all forces except for gravity (such as air resistance and friction, for example) are negligible. The components of acceleration are then very simple: ay=−g=−9.81ms2 (we assume that the motion occurs at small enough heights near the surface of the earth so that the acceleration due to gravity is constant). Because the acceleration due to gravity is along the vertical direction only, ax=0. Thus, the kinematic equations describing the motion along the x and y directions respectively, can be used:
x=x0+vxty=v0y+ayty=y0+v0yt+12ayt2v2y=v20y+2ay(y−y0)
We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. The horizontal motion is simple, because ax=0 and vx is thus constant. The velocity in the vertical direction begins to decrease as an object rises; at its highest point, the vertical velocity is zero. As an object falls towards the Earth again, the vertical velocity increases again in magnitude but points in the opposite direction to the initial vertical velocity. The xx and yy motions can be recombined to give the total velocity at any given point on the trajectory.
Key Points
- Constant velocity means that the object in motion is moving in a straight line at a constant speed.
- This line can be represented algebraically as: x=x0+vt, where x0 represents the position of the object at t=0, and the slope of the line indicates the object’s speed.
- The velocity can be positive or negative, and is indicated by the sign of our slope. This tells us in which direction the object moves.
- Constant acceleration in motion in two dimensions generally follows a projectile pattern.
- Projectile motion is the motion of an object thrown or projected into the air, subject to only the (vertical) acceleration due to gravity.
- We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes.
Key Terms
- constant velocity: Motion that does not change in speed nor direction.
- kinematic: of or relating to motion or kinematics
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Provided by: Light and Matter. Located at: http://lightandmatter.com/lmb.pdf. License: CC BY: Attribution
- Velocity. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Velocity. License: CC BY-SA: Attribution-ShareAlike
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/constant-velocity. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Light and Matter. Located at: http://lightandmatter.com/lmb.pdf. License: CC BY: Attribution
- Acceleration. Provided by: Wikipedia. Located at: http://en.Wikipedia.org/wiki/Acceleration. License: CC BY-SA: Attribution-ShareAlike
- OpenStax College, College Physics. September 17, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42042/latest/?collection=col11406/1.7. License: CC BY: Attribution
- kinematic. Provided by: Wiktionary. Located at: http://en.wiktionary.org/wiki/kinematic. License: CC BY-SA: Attribution-ShareAlike
- Provided by: Light and Matter. Located at: http://lightandmatter.com/lmb.pdf. License: CC BY: Attribution
- OpenStax College, College Physics. October 19, 2012. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42042/latest/?collection=col11406/1.7. License: CC BY: Attribution

