11.3: Bernoulli’s Equation
- Last updated
- Jan 14, 2019
- Save as PDF
- Page ID
- 17001

- Boundless
- Boundless
( \newcommand{\kernel}{\mathrm{null}\,}\)
learning objectives
- Adapt Bernoulli’s equation for flows that are either unsteady or compressible
Application of Bernoulli’s Equation
The relationship between pressure and velocity in ideal fluids is described quantitatively by Bernoulli’s equation, named after its discoverer, the Swiss scientist Daniel Bernoulli (1700–1782). Bernoulli’s equation states that for an incompressible and inviscid fluid, the total mechanical energy of the fluid is constant. (An inviscid fluid is assumed to be an ideal fluid with no viscosity. )
Bernoulli’s Principle: A brief introduction to Bernoulli’s Principle for students studying fluids.
The total mechanical energy of a fluid exists in two forms: potential and kinetic. The kinetic energy of the fluid is stored in static pressure, psps, and dynamic pressure, 12ρV212ρV2, where \rho is the fluid density in (SI unit: kg/m3) and V is the fluid velocity (SI unit: m/s). The SI unit of static pressure and dynamic pressure is the pascal.
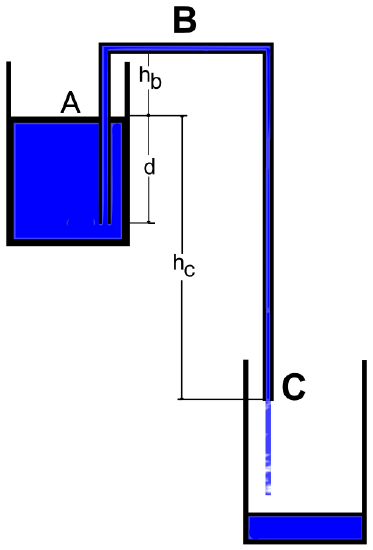
Syphoning: Syphoning fluid between two reservoirs. The flow rate out can be determined by drawing a streamline from point ( A ) to point ( C ).
Static pressure is simply the pressure at a given point in the fluid, dynamic pressure is the kinetic energy per unit volume of a fluid particle. Thus, a fluid will not have dynamic pressure unless it is moving. Therefore, if there is no change in potential energy along a streamline, Bernoulli’s equation implies that the total energy along that streamline is constant and is a balance between static and dynamic pressure. Mathematically, the previous statement implies:
ps+12ρV2=constant
along a streamline. If changes there are significant changes in height or if the fluid density is high, the change in potential energy should not be ignored and can be accounted for with,
ΔPE=ρgΔh.
This simply adds another term to the above version of the Bernoulli equation and results in
ps+12ρV2+ρgΔh=constant.
Deriving Bernoulli’s Equation
The Bernoulli equation can be derived by integrating Newton’s 2nd law along a streamline with gravitational and pressure forces as the only forces acting on a fluid element. Given that any energy exchanges result from conservative forces, the total energy along a streamline is constant and is simply swapped between potential and kinetic.
Applying Bernoulli’s Equation
Bernoulli’s equation can be applied when syphoning fluid between two reservoirs. Another useful application of the Bernoulli equation is in the derivation of Torricelli’s law for flow out of a sharp edged hole in a reservoir. A streamline can be drawn from the top of the reservoir, where the total energy is known, to the exit point where the static pressure and potential energy are known but the dynamic pressure (flow velocity out) is not.
Adapting Bernoulli’s Equation
The Bernoulli equation can be adapted to flows that are both unsteady and compressible. However, the assumption of inviscid flow remains in both the unsteady and compressible versions of the equation. Compressibility effects depend on the speed of the flow relative to the speed of sound in the fluid. This is determined by the dimensionless quantity known as the Mach number. The Mach number represents the ratio of the speed of an object moving through a medium to the speed of sound in the medium.
Torricelli’s Law
Torricelli’s law is theorem about the relation between the exit velocity of a fluid from a hole in a reservoir to the height of fluid above the hole.
learning objectives
- Infer the exit velocity through examining the Bernoulli equation
Torricelli’s law is theorem in fluid dynamics about the relation between the exit velocity of a fluid from a sharp-edged hole in a reservoir to the height of the fluid above that exit hole. This relationship applies for an “ideal” fluid (inviscid and incompressible) and results from an exchange of potential energy,
Torricelli’s Principle: A brief introduction to Torricelli’s Principle for students studying fluids.
mghmgh, for kinetic energy,
12ρv2, at the exit.
This relationship can be derived by applying the Bernoulli equation between the top of the reservoir and the exit hole. Applying Bernoulli between the top of a reservoir and an exit hole at a height h below the top of the reservoir results in,
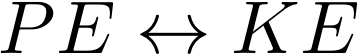
Exchange of Energy: Potential energy at the top of the reservoir becomes kinetic energy at the exit.
pt+12ρv2t+ρght=pe+12ρv2e+ρghe
where subscript t implies evaluation at the top of the reservoir and subscript e implies evaluation at the exit. If we assume both the top of reservoir and the exit are open to the atmosphere, the zero for potential energy is at the exit hole, and the fluid velocity at the top of the reservoir is essentially zero (large reservoir, small hole), we arrive at
ρght=12ρv2e
This can be solved for the exit velocity, resulting in,
ve=√2ght
where again ht is the height difference between the top of the reservoir and the exit hole. Due to the assumption of an ideal fluid, all forces acting on the fluid are conservative and thus there is an exchange between potential and kinetic energy. The result is that the velocity acquired by the fluid is the same that a body would acquire when simply dropped from the height ht.
A simple experiment to test Torricelli’s law involves filling a soda bottle with water and puncturing the bottom with a small hole (about 1 cm in diameter). As the height in the reservoir decreases, the exit velocity will decrease as well. The exit velocity can be increased by capping the top of the reservoir and pressurizing it.
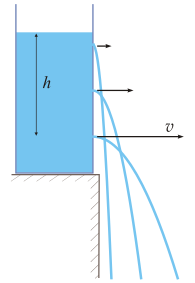
Toricelli’s Law: The exit velocity depends on the height of the fluid above the exit hole.
Ideal Fluid: Applies to an ideal fluid (inviscid, incompressible)
Surface Tension
The tendency of the surface of a liquid to resist a force and behave like a membrane and is a result of cohesion between liquid molecules.
learning objectives
- Summarize the cause for different surface tensions at a liquid’s surface
Surface tension is the tendency of a liquid surface to resist forces applied to it. This effect is a result of cohesion of the molecules of the liquid causing the surface of the liquid to contract to the smallest area possible. This effect is visible in nature with water strider insects that are able to walk on water. Also, a paper clip or pin can be supported by the surface tension at a water air interface.
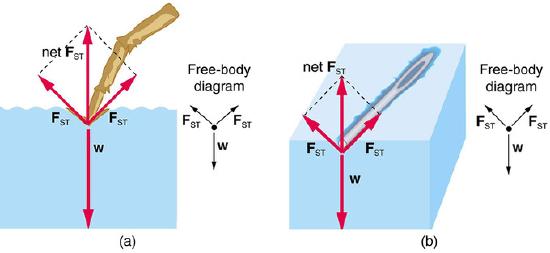
Surface Tension FBD: Force diagrams showing the direction of forces for water supporting a water strider (insect) foot and a pin. In both cases, the vertical component of the surface tension is enough to support the weight of the object.
In the bulk of the liquid, the molecules are pulled equally in all directions. The molecules at the surface feel a greater attractive force toward the bulk material than the interface material.
The surface of a liquid is an interface between another fluid, a solid body, or both. Therefore, the surface tension will be a property of the interface rather than simply the liquid. Adhesion describes the attractive force between molecules of different types. The surface of a liquid in a container is an interface between the liquid, the air, and the container. Where the surfaces meet, forces must be in equilibrium. This results in a contact angle at the interface. The contact angle is measured in the liquid and depends on the relative strength of cohesive forces in the liquid and adhesive forces between the liquid and interface materials. If liquid molecules are strongly attracted to the molecules of the solid surface (adhesive forces > cohesive forces), the drop will tend to spread out and the contact angle will be close to zero degrees. If the cohesive forces are greater than the adhesive forces, the resulting contact angles will be large and will form a more circular drop.

Water Droplet on Leaf: When a water droplet forms on a leaf, the cohesive forces between the water molecules are greater than the adhesive forces between the water and leaf surface. The leaf is a hydrophobic surface.
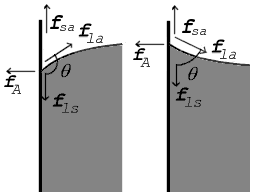
Contact Angle: The contact angle is the angle, measured in the fluid, that results when a liquid-gas interface, meets a solid surface.
When the liquid is water, a surface where the contact angle is small is said to be hydrophilic. Large contact angles are present on hydrophobic surfaces. The contact angle determines the wettability of the surface.
Key Points
- The simplest form of Bernoulli’s equation (steady and incompressible flow) states that the sum of mechanical energy, potential energy and kinetic energy, along a streamline is constant. Therefore, any increase in one form results in a decrease in the other.
- Bernoulli’s equation considers only pressure and gravitational forces acting on the fluid particles. Therefore, if there is no change in height along a streamline, Bernoulli’s equation becomes a balance between static pressure and velocity.
- The steady-state, incompressible Bernoulli equation, can be derived by integrating Newton’s 2nd law along a streamline.
- Torricelli’s law applies to an inviscid, incompressible fluid (“ideal” fluid).
- You can ascertain results from applying the Bernoulli equation between the top of the reservoir and the exit hole.
- The relationship arises from an exchange of potential energy at the top of the reservoir to kinetic energy at the exit.
- The final kinetic energy is equivalent to what a solid body would acquire when falling from height h.
- Surface tension is a result of cohesion between the molecules of the liquid. The molecules at the surface of the liquid feel an attractive force pulling them toward the bulk of the liquid more than the solid or fluid at the interface.
- When a liquid-solid-gas interface is encountered, the contact angle represents a measure of the relative strength of adhesive and cohesive forces.
- The contact angle determines the wettability of a surface.
Key Terms
- viscosity: A quantity expressing the magnitude of internal friction in a fluid, as measured by the force per unit area resisting uniform flow.
- Ideal Fluid: An inviscid and incompressible fluid
- incompressible: Unable to be compressed or condensed.
- inviscid: A fluid with zero viscosity (internal friction). In reality viscosity is always present. However, it is often very small compared with other forces (e.g. gravity, pressure) and for common fluids (water and air) the fluid can be approximated as having zero viscosity.
- cohesion: Various intermolecular forces that hold solids and liquids together.
- wettability: The ability of a solid surface to reduce the surface tension of a liquid in contact with it such that it spreads over the surface and wets it.
- adhesion: The ability of a substance to stick to an unlike substance.
LICENSES AND ATTRIBUTIONS
CC LICENSED CONTENT, SHARED PREVIOUSLY
- Curation and Revision. Provided by: Boundless.com. License: CC BY-SA: Attribution-ShareAlike
CC LICENSED CONTENT, SPECIFIC ATTRIBUTION
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/ideal-fluid. License: CC BY-SA: Attribution-ShareAlike
- incompressible. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/incompressible. License: CC BY-SA: Attribution-ShareAlike
- viscosity. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/viscosity. License: CC BY-SA: Attribution-ShareAlike
- Syphoning2. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Syphoning2.svg. License: Public Domain: No Known Copyright
- Bernoulli's Principle. Located at: http://www.youtube.com/watch?v=57OB21-I2lQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Boundless. Provided by: Boundless Learning. Located at: www.boundless.com//physics/definition/inviscid. License: CC BY-SA: Attribution-ShareAlike
- Syphoning2. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Syphoning2.svg. License: Public Domain: No Known Copyright
- Bernoulli's Principle. Located at: http://www.youtube.com/watch?v=57OB21-I2lQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5b/TorricelliLaw.svg/200px-TorricelliLaw.svg.png. License: Public Domain: No Known Copyright
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5106d670e4b010f3dd6d22de/ideal.png. License: Public Domain: No Known Copyright
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5106d406e4b010f3dd6d22c1/peke.png. License: Public Domain: No Known Copyright
- Torricelli's Principle. Located at: http://www.youtube.com/watch?v=57OB21-I2lQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Surface tension. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/Surface_tension%23Effects_of_surface_tension. License: CC BY-SA: Attribution-ShareAlike
- adhesion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/adhesion. License: CC BY-SA: Attribution-ShareAlike
- cohesion. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/cohesion. License: CC BY-SA: Attribution-ShareAlike
- wettability. Provided by: Wiktionary. Located at: en.wiktionary.org/wiki/wettability. License: CC BY-SA: Attribution-ShareAlike
- Syphoning2. Provided by: Wikimedia. Located at: commons.wikimedia.org/wiki/File:Syphoning2.svg. License: Public Domain: No Known Copyright
- Bernoulli's Principle. Located at: http://www.youtube.com/watch?v=57OB21-I2lQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Provided by: Wikimedia. Located at: http://upload.wikimedia.org/Wikipedia/commons/thumb/5/5b/TorricelliLaw.svg/200px-TorricelliLaw.svg.png. License: Public Domain: No Known Copyright
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5106d670e4b010f3dd6d22de/ideal.png. License: Public Domain: No Known Copyright
- Boundless. Provided by: Amazon Web Services. Located at: s3.amazonaws.com/figures.boundless.com/5106d406e4b010f3dd6d22c1/peke.png. License: Public Domain: No Known Copyright
- Torricelli's Principle. Located at: http://www.youtube.com/watch?v=57OB21-I2lQ. License: Public Domain: No Known Copyright. License Terms: Standard YouTube license
- Erik Christensen, College Physics II. February 5, 2013. Provided by: OpenStax CNX. Located at: http://cnx.org/content/m42197/latest/?collection=col11458/1.2. License: CC BY: Attribution
- SurfTensionContactAngle. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:SurfTensionContactAngle.png. License: Public Domain: No Known Copyright
- Dew 2. Provided by: Wikipedia. Located at: en.Wikipedia.org/wiki/File:Dew_2.jpg. License: Public Domain: No Known Copyright


