4.3: Lensing

When a photon passes a massive object, the path of the photon is deflected. If the impact parameter is small, the photon may be deflected and collide with the massive object (or fall into the singularity), or the photon may "swing around" the massive object (possibly multiple times) and escape. A quantitative calculation of the path is beyond the scope of this course. In the last section, we discussed a method to get qualitative information about the path. In this section, we will look at how to get quantitative information about the light path under very specific conditions. Specifically, in this section we are going to assume that:

1. the source of the light is very far from the gravitational lens
2. the gravitational lens is very far from the observer
3. the lensing object is between the source and the observer
4. the light travels in a straight line from the source to the lens, then suddenly turns and travels in another straight line to the observer

Definition: Gravitational Lens

A gravitational lens is a distribution of mass that causes light to bend around it.

Figure $\PageIndex{1}$: Light from a source (solid circle) travels in a straight line to the lensing plane, then turns and enters the observer's eye. Dashed lines show where the observer will think the light is coming from (i.e. the image location). Note that this is only a 2D depiction. There will also be paths that come out of or go into the page and then bend back to the observer, which will cause the image to be smeared out over a ring instead of two points. (Krishnavedala, CC0, via Wikimedia Commons)

Figure $\PageIndex{1}$ illustrates the lensing process and defines key distances and angles. They are:

$$\begin{align*}D_L&=\text{distance from observer to lens}\\ D_S&=\text{distance from observer to source}\\ D_{LS}&=\text{distance from lens to source}\\ \theta_S&=\text{angle between line of sight to lens and line of sight to source}\\ \theta_1&=\text{angle between line of sight to lens and line of sight to image}\end{align*}$$

As illustrated in the figure, there are two possible light paths from the source that will reach the observer's eye. The dashed lines show where the observer will think the light is coming from, which is where the images will appear. But this only shows the paths of light in one plane. There are also light beams that come out of the page that will bend back and enter the observer's eye. And there are light beams that go into the page that will will bend back and enter the observer's eye. The result is that the image of the source appears to be smeared out over a ring, called an Einstein ring. Figure $\PageIndex{2}$ shows a cartoon depiction of an Einstein ring, and Figure $\PageIndex{3}$ shows an actual image from the Hubble telescope with an Einstein ring.

Figure $\PageIndex{2}$: A cartoon depiction of an Einstein ring. (ALMA (ESO/NRAO/NAOJ), L. Calçada (ESO), Y. Hezaveh et al., CC BY 4.0, via Wikimedia Commons)

Figure $\PageIndex{3}$: An actual Einstein ring. (ESA/Hubble, CC BY 4.0, via Wikimedia Commons)

The angular size $\theta_E$ of the Einstein ring is given by

$$\theta_E=\sqrt{\frac{4MD_{LS}}{D_LD_S}}. \qquad (\text{radians})\label{eq:EinsteinRingAngle}$$

The angles of the two images in the plane are

$$\theta_1=\frac{\theta_S}{2}\pm \frac{1}{2}\sqrt{\theta_S^2+4\theta_E^2}.\label{eq:ObservationAngle}$$

Exercise $\PageIndex{1}$

Given that the Einstein ring is a circle, why is $\theta_E$ not just 360 degrees or $2\pi$ radians? Why is the size measured as an angle instead of a length?

Answer

Figure 4.3.4 shows how an object on the sky fills out a portion of a circle for which the observer is at the center. The angular diameter refers to the portion of the large "celestial sphere" on which the object falls. The Einstein ring angle $\theta_E$ is half of the angular diameter.

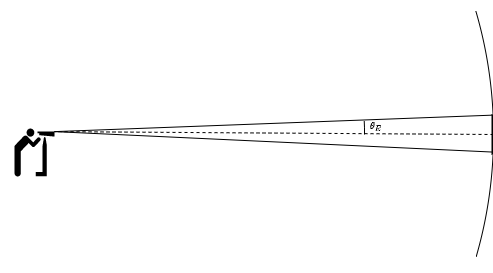
Figure $\PageIndex{4}$: The angular size of the ring refers to the angle that the ring makes on the celestial sphere where the observer is the center. The Einstein ring angle if half the angular diameter. (Copyright; author via source)

The reason the size is given as an angle instead of a length is because the actual diameter of the ring depends on how far away it is, which we don't observe directly. The directly observable quantity is the angle.

Exercise $\PageIndex{2}$

Which, if any, of the angles $\theta_1$ and/or $\theta_E$ depends on whether the lens, source, and observer are colinear? Under what conditions is the observation angle equal to the Einstein ring angle?

Answer

The quantity that captures whether the observer, lens, and source are colinear is the source angle $\theta_S$. The Einstein ring angle does not depend on $\theta_S$, but the observation angle $\theta_1$ does.

If $\theta_S=0$, then the observation angle and the Einstein ring angle are the same.

The Einstein ring angle tells you the size of the ring, but not where to look to find it. The observation angle $\theta_1$ tells you where to look.

Exercise $\PageIndex{3}$

One of the applications of gravitational lensing is using the size of an Einstein ring to deduce the amount of mass in the lensing object. This requires knowing the distances to the lensing object and the source of the light, which is its own challenge. For now, let's assume we know that the distance from earth to the lensing object is 2 billion light years, and from earth to the light source is 6 billion light years. The angular size of the Einstein ring $\theta_E$ is 1 arcsecond (there are 60 arcminutes in a degree and 60 arcseconds in an arcminute). Calculate the mass of the lensing object in units of the mass of the sun.

Answer

The given distances are $D_L= 2$ billion light years and $D_S=6$ billion light years, which means that $D_{LS}=4$ billion light years. We can solve Equation $\ref{eq:EinsteinRingAngle}$ for $M$ and substitute the known values.

$$M=\frac{\theta_E^2D_LD_S}{4D_{LS}}\nonumber$$

We also need to convert the angle to radians.

$$1\text{ arcsecond}\times\frac{1\text{ arcminute}}{60\text{ arcsecond}}\times\frac{1\text{ degree}}{60\text{ arcminute}}\times \frac{\pi\text{ rad}}{180\text{ degree}}=4.85\times 10^{-6}\text{ rad}\nonumber$$

When we plug in, we have to be careful with units. The radian units effectively get dropped (since a radian is defined as a ratio of two lengths), but the mass will be in terms of light years.

$$M=\frac{\left(4.85\times 10^{-6}\text{ rad}\right)^2(2\text{ billion light years})(6\text{ billion light years})}{4(4\text{ billion light years})}=1.76\times 10^{-11}\text{ billion light years}\nonumber$$

Previously we learned that the mass of the sun is $1477\text{ m}.$ We also know that the conversion between distance and time is $1\text{ s}=3\times 10^8\text{ m}$. We can use these to convert the mass of the lensing object to solar masses, $M_\odot$.

$$1.76\times 10^{-11}\text{ billion light years}=1.76\times 10^{-2}\text{ light years}\times \frac{3.154\times 10^7\text{ s}}{1\text{ year}}\times \frac{3\times 10^8\text{ m}}{1\text{ s}}\times \frac{1 M_\odot}{1477\text{ m}}=1.13\times 10^{10}M_\odot\nonumber$$

The mass of the lensing object is equivalent to about 10 billion suns, which is like a small galaxy.

---

Box $\PageIndex{1}$

The "Cosmic Horseshoe" (Fig. 4.3.5) is a name given to an Einstein ring resulting from a gravitational lens in the Leo constellation. The lensing galaxy is 5.2 billion light-years from earth while the source galaxy is 10.3 billion light-years from earth.

Figure $\PageIndex{5}$:The Cosmic Horseshoe. (Image credit: https://home.strw.leidenuniv.nl/~jarle/Teaching/Practicum2015/assets/2015-04-19-einstein-ring.pdf)

1. Use the image in Figure $\PageIndex{5}$ as well as the gravitational lens equations to approximate the mass of the lensing galaxy.
2. Given the position of the ring relative to the lensing galaxy, what can you say about the position of the source galaxy relative to the lensing galaxy? In other words, is earth colinear with the two galaxies?