6.7: Cohesion and Adhesion in Liquids - Surface Tension and Capillary Action

Learning Objectives

By the end of this section, you will be able to:

• Understand cohesive and adhesive forces.
• Define surface tension.
• Understand capillary action.

Children blow soap bubbles and play in the spray of a sprinkler on a hot summer day (Figure \(\PageIndex{1}\)). An underwater spider keeps his air supply in a shiny bubble he carries wrapped around him. A technician draws blood into a small-diameter tube just by touching it to a drop on a pricked finger. A premature infant struggles to inflate her lungs. What is the common thread? All these activities are dominated by the attractive forces between atoms and molecules in liquids—both within a liquid and between the liquid and its surroundings.

Figure \(\PageIndex{1}\):The soap bubbles in this photograph are caused by cohesive forces among molecules in liquids. (credit: Steve Ford Elliott)

Attractive forces between molecules of the same type are called cohesive forces. Liquids can, for example, be held in open containers because cohesive forces hold the molecules together. Attractive forces between molecules of different types are called adhesive forces. Such forces cause liquid drops to cling to window panes, for example. In this section we examine effects directly attributable to cohesive and adhesive forces in liquids.

Definition: Cohesive Forces

Attractive forces between molecules of the same type are called cohesive forces.

Definition: Adhesive Forces

Attractive forces between molecules of different types are called adhesive forces.

Surface Tension

Cohesive forces between molecules cause the surface of a liquid to contract to the smallest possible surface area. This general effect is called surface tension. Molecules on the surface are pulled inward by cohesive forces, reducing the surface area. Molecules inside the liquid experience zero net force, since they have neighbors on all sides.

Definition: Surface Tension

Cohesive forces between molecules cause the surface of a liquid to contract to the smallest possible surface area. This general effect is called surface tension.

Surface Tension

Forces between atoms and molecules underlie the macroscopic effect called surface tension. These attractive forces pull the molecules closer together and tend to minimize the surface area. This is another example of a submicroscopic explanation for a macroscopic phenomenon.

The model of a liquid surface acting like a stretched elastic sheet can effectively explain surface tension effects. For example, some insects can walk on water (as opposed to floating in it) as we would walk on a trampoline—they dent the surface as shown in Figure \(\PageIndex{2a}\). Figure \(\PageIndex{2b}\) shows another example, where a needle rests on a water surface. The iron needle cannot, and does not, float, because its density is greater than that of water. Rather, its weight is supported by forces in the stretched surface that try to make the surface smaller or flatter. If the needle were placed point down on the surface, its weight acting on a smaller area would break the surface, and it would sink.

Figure \(\PageIndex{2}\): Surface tension supporting the weight of an insect and an iron needle, both of which rest on the surface without penetrating it. They are not floating; rather, they are supported by the surface of the liquid. (a) An insect leg dents the water surface. \(F_{ST}\) is a restoring force (surface tension) parallel to the surface. (b) An iron needle similarly dents a water surface until the restoring force (surface tension) grows to equal its weight.

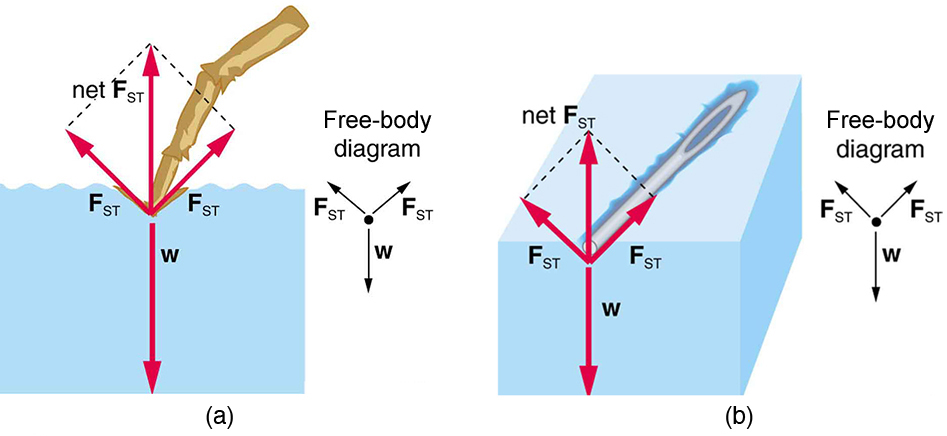
Surface tension is proportional to the strength of the cohesive force, which varies with the type of liquid. Surface tension \(\overline{\gamma}\) is defined to be the force F per unit length \(L\) exerted by a stretched liquid membrane:

\[\gamma = \dfrac{F}{L}.\]

Table \(\PageIndex{1}\) lists values of \(\overline{\gamma}\) for some liquids.

Table \(\PageIndex{1}\)

Liquid	Surface tension γ(N/m)
Water at \(0^oC\)	0.0756
Water at \(20^oC\)	0.0728
Water at \(100^OC\)	0.0589
Soapy water (typical)	0.0370
Ethyl alcohol	0.0223
Glycerin	0.0631
Mercury	0.465
Olive Oil	0.032
Tissue fluids (typical)	0.050
Blood, whole at \(37^oC\)	0.058
Blood plasma at \(37^oC\)	0.073
Gold at \(1070^oC\)	1.000
Oxygen at \(-193^oC\)	0.0157
Helium at \(-269^oC\)	0.00012

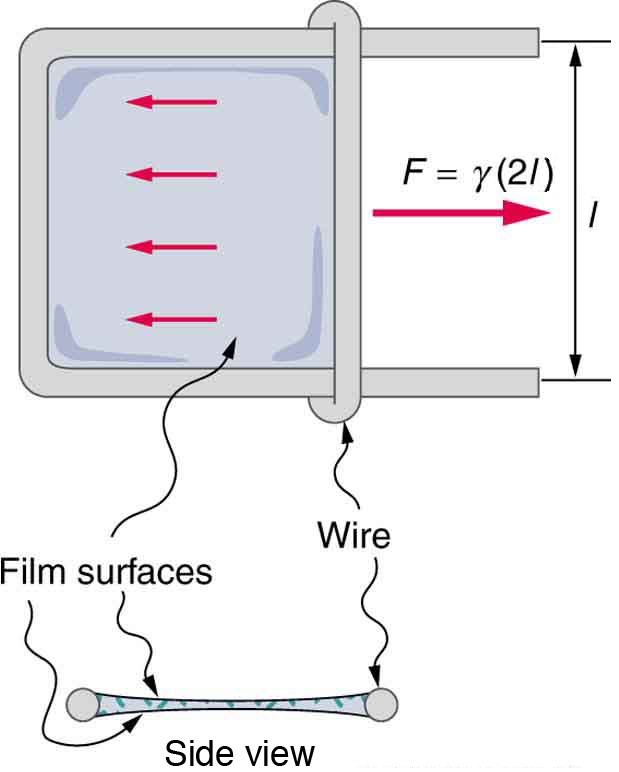
For the insect of Figure Figure \(\PageIndex{1a}\), its weight \(w\) is supported by the upward components of the surface tension force: \(w = \gamma L \sin \theta\), where \(L\) is the circumference of the insect’s foot in contact with the water. Figure \(\PageIndex{3}\) shows one way to measure surface tension. The liquid film exerts a force on the movable wire in an attempt to reduce its surface area. The magnitude of this force depends on the surface tension of the liquid and can be measured accurately.

Figure \(\PageIndex{3}\): Sliding wire device used for measuring surface tension; the device exerts a force to reduce the film’s surface area. The force needed to hold the wire in place is \(F = \gamma L = \gamma (2l)\), since there are two liquid surfaces attached to the wire. This force remains nearly constant as the film is stretched, until the film approaches its breaking point.

Surface tension is the reason why liquids form bubbles and droplets. The inward surface tension force causes bubbles to be approximately spherical and raises the pressure of the gas trapped inside relative to atmospheric pressure outside. It can be shown that the gauge pressure \(P \) inside a spherical bubble is given by

\[P = \dfrac{4\gamma}{r},\]

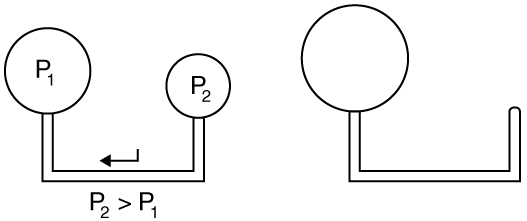
where \(r\) is the radius of the bubble. Thus the pressure inside a bubble is greatest when the bubble is the smallest. Another bit of evidence for this is illustrated in Figure \(\PageIndex{4}\). When air is allowed to flow between two balloons of unequal size, the smaller balloon tends to collapse, filling the larger balloon.

Figure \(\PageIndex{4}\): With the valve closed, two balloons of different sizes are attached to each end of a tube. Upon opening the valve, the smaller balloon decreases in size with the air moving to fill the larger balloon. The pressure in a spherical balloon is inversely proportional to its radius, so that the smaller balloon has a greater internal pressure than the larger balloon, resulting in this flow.

Example \(\PageIndex{1}\): Surface Tension: Pressure Inside a Bubble

Calculate the gauge pressure inside a soap bubble \(2.00 \times 10^{-4} m\) in radius using the surface tension for soapy water in Table. Convert this pressure to mm Hg.

Strategy

The radius is given and the surface tension can be found in Table, and so \(P\) can be found directly from the equation \(P = \frac{4\gamma}{r}\).

Solution

Substituding \(r\) and \(\gamma\) into this equation \(P = \frac{4\gamma}{r}\), we obtaiin

\[P = \dfrac{4\gamma}{r} = \dfrac{4(0.037 \, N/m)}{2.00 \times 10^{-4}m} = 740 \, N/m^2 = 740 \, Pa.\]

We use a conversion factor to get this into units of mm Hg:

\[P = (740 \, N/m^2)\dfrac{1.00 \, mm \, Hg}{133 \, N/m^2} = 5.56 \, mm \, Hg.\]

Discussion

Note that if a hole were to be made in the bubble, the air would be forced out, the bubble would decrease in radius, and the gauge pressure would reduce to zero, and the absolute pressure inside would decrease to atmospheric pressure (760 mm Hg).

Our lungs contain hundreds of millions of mucus-lined sacs called alveoli, which are very similar in size, and about 0.1 mm in diameter. (See Figure.) You can exhale without muscle action by allowing surface tension to contract these sacs. Medical patients whose breathing is aided by a positive pressure respirator have air blown into the lungs, but are generally allowed to exhale on their own. Even if there is paralysis, surface tension in the alveoli will expel air from the lungs. Since pressure increases as the radii of the alveoli decrease, an occasional deep cleansing breath is needed to fully reinflate the alveoli. Respirators are programmed to do this and we find it natural, as do our companion dogs and cats, to take a cleansing breath before settling into a nap.

Figure \(\PageIndex{5}\): Bronchial tubes in the lungs branch into ever-smaller structures, finally ending in alveoli. The alveoli act like tiny bubbles. The surface tension of their mucous lining aids in exhalation and can prevent inhalation if too great.

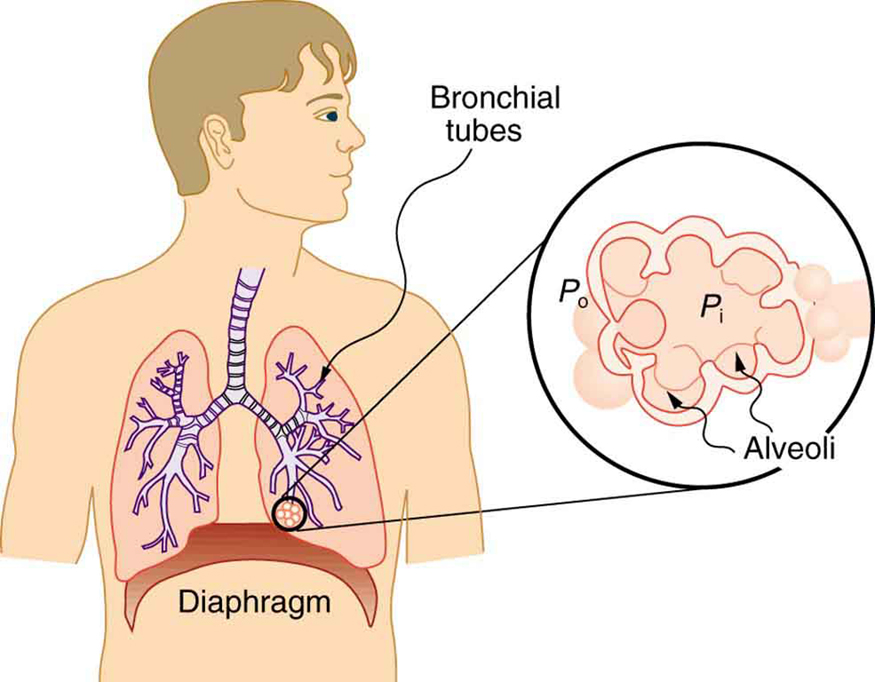
The tension in the walls of the alveoli results from the membrane tissue and a liquid on the walls of the alveoli containing a long lipoprotein that acts as a surfactant (a surface-tension reducing substance). The need for the surfactant results from the tendency of small alveoli to collapse and the air to fill into the larger alveoli making them even larger (as demonstrated in Figure). During inhalation, the lipoprotein molecules are pulled apart and the wall tension increases as the radius increases (increased surface tension). During exhalation, the molecules slide back together and the surface tension decreases, helping to prevent a collapse of the alveoli. The surfactant therefore serves to change the wall tension so that small alveoli don’t collapse and large alveoli are prevented from expanding too much. This tension change is a unique property of these surfactants, and is not shared by detergents (which simply lower surface tension). (See Figure.)

Figure \(\PageIndex{6}\): Surface tension as a function of surface area. The surface tension for lung surfactant decreases with decreasing area. This ensures that small alveoli don’t collapse and large alveoli are not able to over expand.

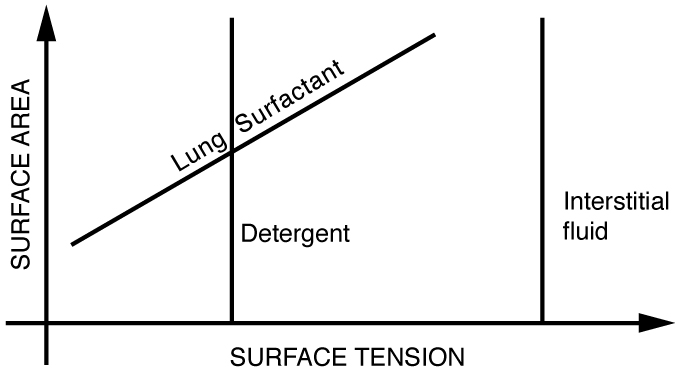
If water gets into the lungs, the surface tension is too great and you cannot inhale. This is a severe problem in resuscitating drowning victims. A similar problem occurs in newborn infants who are born without this surfactant—their lungs are very difficult to inflate. This condition is known as hyaline membrane disease and is a leading cause of death for infants, particularly in premature births. Some success has been achieved in treating hyaline membrane disease by spraying a surfactant into the infant’s breathing passages. Emphysema produces the opposite problem with alveoli. Alveolar walls of emphysema victims deteriorate, and the sacs combine to form larger sacs. Because pressure produced by surface tension decreases with increasing radius, these larger sacs produce smaller pressure, reducing the ability of emphysema victims to exhale. A common test for emphysema is to measure the pressure and volume of air that can be exhaled.

Making Connections: Take-Home Investigation

1. Try floating a sewing needle on water. In order for this activity to work, the needle needs to be very clean as even the oil from your fingers can be sufficient to affect the surface properties of the needle.
2. Place the bristles of a paint brush into water. Pull the brush out and notice that for a short while, the bristles will stick together. The surface tension of the water surrounding the bristles is sufficient to hold the bristles together. As the bristles dry out, the surface tension effect dissipates.
3. Place a loop of thread on the surface of still water in such a way that all of the thread is in contact with the water. Note the shape of the loop. Now place a drop of detergent into the middle of the loop. What happens to the shape of the loop? Why?
4. Sprinkle pepper onto the surface of water. Add a drop of detergent. What happens? Why?
5. Float two matches parallel to each other and add a drop of detergent between them. What happens? Note: For each new experiment, the water needs to be replaced and the bowl washed to free it of any residual detergent.

Summary

• Attractive forces between molecules of the same type are called cohesive forces.
• Attractive forces between molecules of different types are called adhesive forces.
• Cohesive forces between molecules cause the surface of a liquid to contract to the smallest possible surface area. This general effect is called surface tension.

Glossary

adhesive forces

the attractive forces between molecules of different type

cohesive forces

the attractive forces between molecules of the same type

surface tension

the cohesive forces between molecules which cause the surface of a liquid to contract to the smallest possible surface area

Contributors and Attributions

Paul Peter Urone (Professor Emeritus at California State University, Sacramento) and Roger Hinrichs (State University of New York, College at Oswego) with Contributing Authors: Kim Dirks (University of Auckland) and Manjula Sharma (University of Sydney). This work is licensed by OpenStax University Physics under a Creative Commons Attribution License (by 4.0).