6.5: Mass Analyzer - Time of Flight
( \newcommand{\kernel}{\mathrm{null}\,}\)
Cell membranes are considered one of the most important structures in biology since they play a critical role in biological processes and medicine. Despite their importance, there are still debatable hypotheses regarding their nature, especially their spatial arrangement of lipid and other membrane bound molecules.1 For example, it is challenging to study lipids with good spatial resolution while not disturbing any important chemical information present on the cell membrane. This article will focus on discussing mass spectrometry, time of flight (ToF, mass detector) and time of flight coupled with secondary ion mass spectrometry (ToF-SIMS) as a tool to study membrane lipids. In recent years, mass spectrometry has been a widely used tool to analyze complex biological systems. In simplified terms, the analysis is carried out by obtaining mass-to-charge (m/z) ratios corresponding to the mass of the atoms or molecules. Figure 6.5.1 displays a flow chart depicting a mass spectrometer system. Here, we will focus on the mass analyzer component of the mass spectrometer system.

Mass Analyzers
It is important to note that each mass analyzer has unique parameters and applications as well as its own limitation. Table 1 shows the different types of mass analyzers. Some mass spectrometers have a single mass analyzer and others have a combination of two, for the purpose of improving its analytical performance.2 These are known as hybrid mass spectrometers and have a combination of mass analyzers such as a quadrupole coupled with a time of flight (QToF). Hybrid QToF mass spectrometers have the capability of performing tandem mass spectrometry or MS/MS analysis. In MS/MS analysis, primary ions are selected to transmit through the first mass analyzer. Then these primary ions are fragmented to produce secondary ions in a collision unit and lastly are analyzed by the second mass analyzer. This secondary analysis produces characteristic ion fragments and this results in increased selectivity and sensitivity.3

Table 1. Types of mass analyzers with their distinct parameters.4
Time of Flight (ToF)
The mass analyzer this article will focus on is, time-of-flight (ToF). The principle of ToF mass analyzer involves the separation of ions based on the time it takes for the ions to travel through a flight tube with known length and reach the detector.2 The trajectory of the ions through a ToF mass analyzer depends on its momentum and kinetic energy due to an applied pulsed acceleration voltage and m/z ratios of the ions.2 Based on classical physics, ions with lower m/z will travel the fastest and arrive at the detector first while ions with larger m/z will travel the slowest and arrive at the detector last. A ToF layout is shown in Figure 6.5.2.

The following derivation to describe a ToF analyzer dynamics was adapted from Hoffman et al 2007.4 The time it takes for the ions to move across the flight tube between the ion source and detector allows us to determine the m/z ratios.4 In the ToF spectrum, the recorded peak for any m/z will correspond to the sum of signals corresponding to multiple and independent ions arriving at the mass detectror. This can be shown in the following equations where the potential energy given to ions in the accelerated regions is converted to kinetic energy for all ions:
zeVs⏟potential energy=12mv2⏟kinetic energy
Next, we solve the equated equations above for velocity v.
v=√2ezVsm
Since velocity is equal to the drift path length divided by time we get:
v=Lt⇒t=Lv
Then solving for time and we get the following equation used to described time in a ToF analyzer.
t=√(mz)(L22eVs)
By algebraically rearranging the equation above, an expression of m/z is determined as shown below.
mz=(2eVsL2)t2
We can also describe mass resolution for ions by differentiating the equation above with respect to mass and time we get the following relation:
1zdm=(2eVsL2)2tdt
Manipulating the equation above, we get the following relation used to express mass resolution.
mdm=t2dt⇒t2Δt=mΔm=R, mass resolution
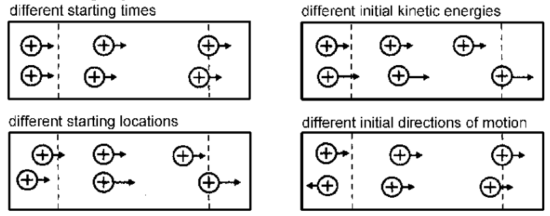
One of the draw backs for using a linear ToF is poor mass resolution.4 Factors that causes poor mass resolution are shown in Figure 6.5.3. The starting times and locations of ions before they are accelerated into the flight tube are different and affect resolution. In addition, different kinetic energies for ions and initial orientation of ion also affect mass resolution and give poor results.
To correct for poor mass resolution, a reflectron is added to the ToF analyzer. A layout of a reflectron ToF is shown in Figure 6.5.4. This type of ToF is sometimes abbreviated as ReTOF.5

There is applied potential in the reflectron, in which reflects ions in the opposite direction to the detector.5 The ions shown in Figure 6.5.4 have similar spacing distances before they arrive at the reflectron and after the reflectron the ions are further apart. The reason for this is due to the difference in kinetic energy the ions carry. Heavier m/z ions have more kinetic energy than lighter m/z ions before and after the reflectron. Therefore, heavier ions will take longer to reach the detector and the lighter ions will reach the detector the quickest. The difference in time for the ions flight trajectory is proportional to the m/z of the ion. An example of enhanced mass resolution is shown in Figure 6.5.5.

Secondary Ion Mass Spectrometry and ToF (ToF-SIMS)
The technique of Secondary Ion Mass Spectrometry (SIMS) has been used in biomedical surface imaging for more than three decades due to its inherent high sensitivity associated with mass spectrometric-based techniques.7
Some examples of the techniques include:2
- Static SIMS: used for sub-monolayer elemental analysis
- Dynamic SIMS: used for obtaining compositional information as a function of depth below surface
- Imaging SIMS: used for spatially-resolved elemental analysis
SIMS instrument works by first initiating a primary ion beam, which can generate either positive or negative ions. These ions are focused directly onto the analyte surface producing secondary ions. The secondary ions are transferred into a mass spectrometer across a high electrostatic potential. Figure 6.5.6 shows a simple representation on how SIMS works.8 The ionized elements produced under vacuum from the interaction between the primary ion beam and the analyte are accelerated, focused and analyzed by a mass spectrometer.

There are different designs of SIMS: NanoSIMS, ASI’s SHRIMP, ToF SIMS, etc. Distinguishing between these instruments relies in their difference in intensity, energy and orientation of the primary beam.
Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS) is a surface -sensitive analytical method capable of producing high resolution chemical images. ToF-SIMS is one of the most suitable methods for analysis of lipids attached different to cell membranes and biological materials in general.9 The method uses a high energy primary ion beam (e.g Au3+, Cs+) with pulses of 1 to 40 keV. The primary ion beam remove particles from the outermost surface of the sample causing desorption of secondary ions (SIMS method) as Figure 6.5.7 illustrates. Distinctively, in ToF coupled with SIMS, the particles accelerate into a “flight tube” (ToF method) where they are detected based on the exact time they reach the detector (time-of-flight).10

ToF-SIMS Imaging of Lipids in Cell Membranes
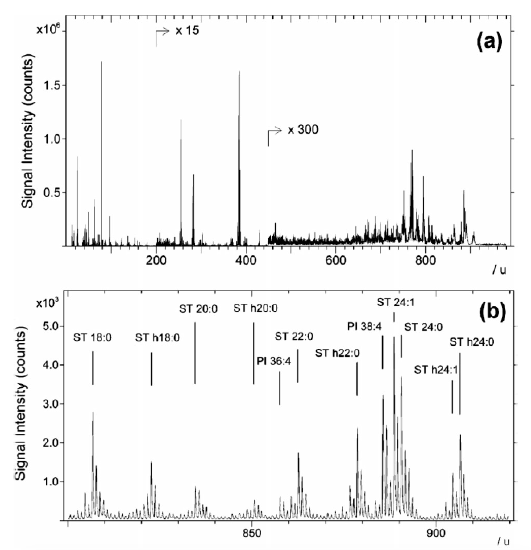
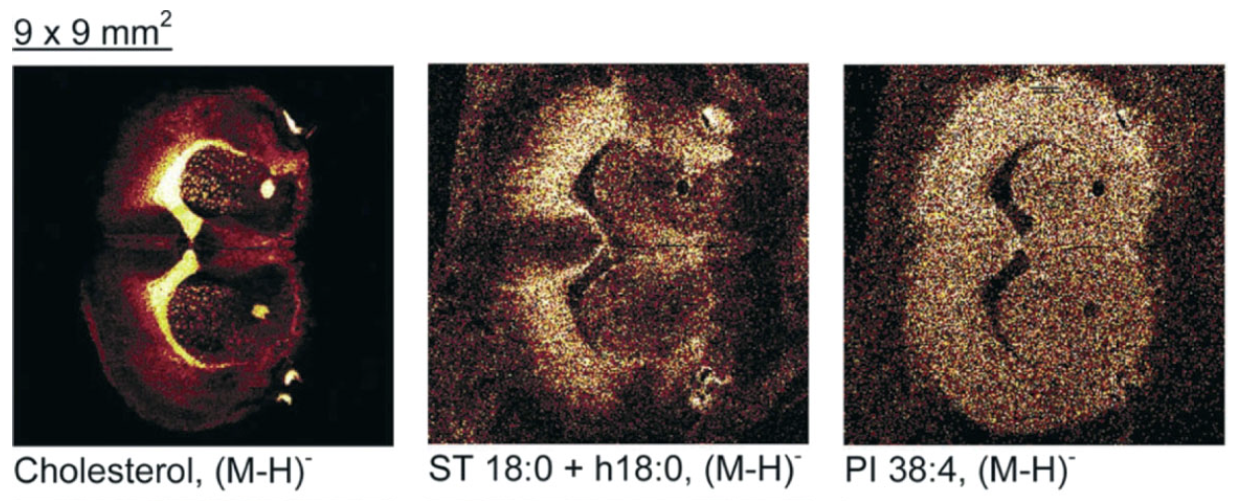
Figure 6.5.8. Examples of ToF-SIMS mass spectrum from biological tissue.5 Figure 6.5.9. Examples of ToF-SIMS images from biological tissues.5
Figure 6.5.8 shows the mass spectrum from a section of a freeze-dried mouse brain. The upper graph (8a) shows an overview of the spectrum while the bottom (8b) shows a selected region corresponding to sulfatides and phosphatidylinositols peaks. Figure 6.5.9 shows a freeze-dried mouse brain that was imaged using the primary ion, Au3+. The three different images show three distinct lipids: cholesterol, a sulfatide (ST 18:0 + h18:0) and a phosphatidylinositorl (PI 38:4).5
Conclusion
- Mass spectrometry (MS) is a useful analytical technique to measure the mass to charge ratio of molecules.
- SIMS allows for the examination and characterization of lipids directly from biological materials.
- ToF-SIMS is a surface analysis technique that enhances the resolution in chemical images on biological material to provide an in-depth understanding.
- ToF-SIMS is an emerging platform for lipid-based imaging studies.
References
- Surf. Interface Anal. 2006; 38: 1401–1412
- Greaves, J.; Roboz, J., Mass spectrometry for the novice. CRC Press: 2013.
- McLafferty, F. W., Tandem Mass Spectrometry. Science. 1981, 214, 280-287.
- De Hoffmann, E.; Stroobant, V., Mass spectrometry: principles and applications. John Wiley & Sons: 2007.
- Gross, J. H., Mass spectrometry: a textbook. Springer Science & Business Media: 2006.
- Loo, J. A., Studying noncovalent protein complexes by electrospray ionization mass spectrometry. Mass spectrometry reviews 1997, 16 (1), 1-23.
- 5.5 Secondary Ion Mass Spectrometry, Miller Index Notation
- Holec, M., Kléma, J., Železný, F., Bělohradský, J., & Tolar, J. (2009). Cross-genome knowledge-based expression data fusion. In International Conference on Bioinformatics, Computational Biology, Genomics and Chemoinformatics, BCBGC 2009 (pp. 43-50).
- Biochim Biophys Acta. 2011 November ; 1811(11): 976–990. doi:10.1016/j.bbalip.2011.05.007 .
- Benninghoven, A., Chemical Analysis of INorganic and Organic Surfaces and Thin Films by Static Time-of-Flight Secondary Ion Mass Spectrometry (ToF-SIMS), 1994, Angewandte Chemie International (in English), vol 33 #10, 1023-1043.