6.4: The Second Law of Thermodynamics
- Last updated
- Nov 8, 2022
- Save as PDF
- Page ID
- 27789
( \newcommand{\kernel}{\mathrm{null}\,}\)
TS Process Diagrams
We have spent a lot of time with PV diagrams because they so clearly relate to the work done in a process through the area under the curve. We have also looked at a number of process diagrams that involve two other state variables. Now that we have added entropy to our arsenal, it's time to get it in on the action. Returning to our original motivation for introducing the entropy – as a way of creating an integral for heat analogous to that for work, it comes to mind that a TS process diagram can do for heat what PV diagrams do for work.
Figure 6.4.1 – Heat Transferred as the Area Under the T vs. S Curve

Q(A→B)=B∫AdQ=B∫ATdS
Interestingly, for a cyclic process, since ΔU=0 (so Q=W), the area inside the closed loop (which for a TS diagram is the total heat transferred), still equals the total work done over the cycle. Another interesting feature is the Carnot cycle that was such an ugly mess on the PV diagram is a nice, easy rectangle on the TS diagram.
Figure 6.4.2 – Carnot Cycle on a TS Diagram

Of course, the nice rectangular (isochoric & isobaric) cycle on the PV diagram becomes quite a mess on the TS diagram, as the Carnot cycle is on the PV diagram.
Multiple Systems
The topic of entropy becomes particularly important when you consider the effect that an exchange of heat or work has on all of the systems involved in the exchange. When we think about these kinds of situations, we need to keep two things in mind:
- The energy lost by one system is gained by the other(s). That is, we are considering only isolated combinations of systems – there is no interplay between the systems in question and the “outside.”
- The entropy function is extensive, which means it is additive when two systems are considered as one.
Consider first two systems that exchange heat reversibly, meaning that their temperatures are infinitesimally close. The entropy change of the two systems combined remains unchanged:
Figure 6.4.3 – Entropy Change for Reversible Heat Exchange
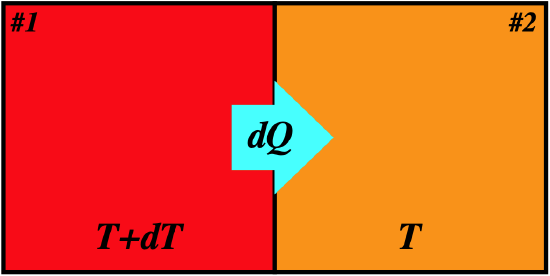
Let's write the heat lost by system #1 and the heat gained by system #2 in terms of the temperatures and entropy changes:
dQ1=T1dS1=(T+dT)dS1dQ2=T2dS2=TdS2
Now we note that the heat gained by system #2 equals the heat lost by system #1 (remember, by assumption these systems do not interact with their surroundings). Also, when comparing a single differential to a product of differentials, the latter vanishes, which means that one of the terms above goes away, leaving:
dQ1=−dQ2⇒TdS1+dTdS1=−TdS2⇒dS1+dS2=d(S1+S2)=dStot=0
So we see that for a reversible transfer of heat, the total entropy of the two systems involved remains unchanged. Recall that we said that the key feature of reversible processes is that the system doesn't carry any "momentum" from one state to the next – every state in the process is in equilibrium, and the process can stop instantly in an equilibrium state. We can now see that the state variable of entropy gives us a way of characterizing thermal equilibrium. Whenever a function satisfies df=0, is means that the function has hit an extremum (a maximum or a minimum). We formally state it this way: A closed system is in a state of thermal equilibrium whenever the entropy function of the system hits an extremum, that is, when dS=0.
The question now becomes, "Is the extremum defined by dS=0 a maximum or a minimum? To answer this, let's look at a case of two systems undergoing an irreversible heat transfer because their temperatures differ by more than an infinitesimal amount.
Figure 6.4.4 – Entropy Change for Irreversible Heat Exchange
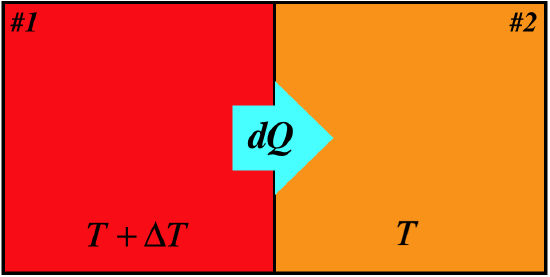
This time with the temperature difference ΔT finite, we don't get the "product of infinitesimals vanishes" situation that we got with the reversible case:
dQ1=T1dS1⇒dS1=dQ1T+ΔTdQ2=T2dS2⇒dS2=dQ2T|dQ|=−dQ1=dQ2}⇒dStot=dS1+dS2=−|dQ|T+ΔT+|dQ|T>0
We see that the change of entropy for the closed system is positive here, which means that for equilibrium the zero change in entropy within the closed system corresponds to a maximum. We therefore make our former statement more specific, and elevate it with its very own pink lettering:
A closed system is in a state of thermal equilibrium if and only if the entropy function of the system is a maximum: dS=0.
The Second Law
The relationship between the entropy state function and thermal equilibrium now established, we can extend it to processes that take place within a closed system. The subsystems within a closed system can exchange work and/or heat to produce processes, and if these are reversible, the entropy of the full system is unchanged, though the entropy of each subsystem can change (one goes up while the other goes down the same amount).
But if the subsystems differ such that the processes they produce are irreversible (due to finite differences in temperature or pressure), then the entropy of the full system will not be a maximum. If a process occurs due to the subsystem imbalance that brings the whole system closer to equilibrium, then the entropy of the whole system must get closer to its maximum – it must go up. Note that the entropy for a single subsystem can go down, but in that case the entropy of the other subsystem must go up more.
Accounting for both the reversible and irreversible cases, we end up with the second law of thermodynamics:
For any process within a closed system, the values of the entropy function at the endpoints of the process satisfy ΔS≥0.
The equality occurs when the process is reversible, and irreversible processes result in an increase of this state variable.
Alert
The most common error made by students when considering the second law is that they focus entirely upon the fact that entropy increases, and forget about the "closed system" requirement. This leads to confusion when a calculation shows that a system's entropy goes down – oftentimes the calculation is correct, but the system under discussion is not actually isolated. This fact can sometimes be quite subtle and hard to see.
A nice way to illustrate the second law is with TS diagrams. Let's consider two thermal reservoirs which directly exchange heat with each other, and are at temperatures that differ by more than an infinitesimal amount and exchange heat. We'll draw TS diagrams for both of these systems side-by side, with the hotter subsystem on the left and the temperature axes on the same scales:
Figure 6.4.5 – TS Diagrams for Thermal Reservoirs Exchanging Heat

As these are thermal reservoirs, their temperatures don't change during this heat exchange. We know that the horizontal line on diagram for the hotter reservoir is higher than that of the cooler reservoir. We also know that the magnitude of the areas under the curves have to be equal, since all the heat that leaves the hotter reservoir enters the cooler one. Therefore the length of the graphs cannot be equal – the length of the segment on the diagram for the cooler reservoir must be longer.
Our sign convention for heat requires that the heat that leaves the hot reservoir is negative (and the integral goes right-to-left), while the heat entering the cooler reservoir is positive. Therefore we have:
|ΔSC|>|ΔSH|ΔSC>0,ΔSH<0}⇒ΔStot=ΔSC+ΔSH>0
The combined entropy of the two reservoirs goes up, because the entropy gain of the colder reservoir is greater than the entropy loss of the hotter reservoir.
Forbidden Cyclic Processes
It was stated without proof in Section 6.2 that engines cannot run in a cycle with only a single thermal reservoir. That is, they must always give up heat to a colder reservoir, forcing them to have less than 100% efficiency. We can now prove this is true with the second law. The engine runs in a cycle, which means that its thermodynamic state returns to the state at which it starts. Since entropy is a state variable, it comes back to where it started, which means that the engine's entropy does not change during the course of a full cycle. The reservoir that provides the heat converted into work by the engine is losing heat, which means that its entropy goes down. If this was the only reservoir, then the closed system of the engine and reservoir would experience a decrease in total entropy, violating the second law. With the addition of a cold reservoir, the heat that goes into it causes its entropy to rise, and the closed system of the engine and both reservoirs avoids having its total entropy go down.
Another forbidden device is a refrigerator that draws heat from a colder reservoir and puts it into a warmer one without work being put in. A refrigerator works in a cycle, so its internal energy (which is a state function) doesn’t change from beginning to end. This means that all of the heat that leaves the colder reservoir enters the warmer one. Therefore with no work put in, the amount of heat that leaves equals the heat that enters. But with a lower temperature and dS=dQT, this means that the colder reservoir loses more entropy than the warmer one gains. The refrigerator’s cycle leaves its entropy unchanged, so this means that the entropy of the closed system consisting of the two reservoirs and the refrigerator has gone down, in contradiction with the second law. But why does the work make a difference, if a work process has no effect on the entropy? Because the energy that comes in as work gets added to the heat that goes into the hot reservoir. This increases the entropy that enters the hot reservoir, compensating for the entropy lost by the cooler reservoir.
Entropy and Efficiency
It is also enlightening to have another look at engine efficiency from the perspective of entropy. The definition of the efficiency of an engine between two thermal reservoirs is given by Equation 6.26. We know that the state of the engine returns to where it started, and entropy is a state function, so for a full cycle it has no change in entropy. Also we assume that the reservoirs do not change temperature, so we can immediately write the heat they gain or lose in terms of their entropy changes:
|QC|=TC|ΔSC|,|QH|=TH|ΔSH|
Plugging these into the engine efficiency formula gives:
e=1−TC|ΔSC|TH|ΔSH|
If all of the processes for the engine are reversible, then the entropy change of the full system (engine and both reservoirs) is zero, which means that the entropy change of the reservoirs are equal in magnitude, which gives:
e=1−TCTH
This was the same result we got for the Carnot cycle, which makes sense, because that cycle allows for constant-temperature reservoirs and reversible processes to coexist (other engines require heat be supplied-to and/or accepted-by a region that keeps changing temperature to stay infinitesimally close to the temperature of the engine).
Now consider what happens to the efficiency if there are irreversible heat exchanges with one or both of the thermal reservoirs (i.e. they have temperatures differing from that of the engine by a finite amount). The entropy of the engine itself still doesn’t change for a cycle, but the entropy of the closed system must get larger. The entropy change of the cold reservoir is positive (heat is going in), and for the hot reservoir it is negative, so to end up with a net positive, the former must exceed the latter. When this happens, the magnitude of the negative second term in the efficiency grows, causing the efficiency to drop. The upshot is that the efficiency given for the Carnot cycle is the maximum possible attainable efficiency for the two reservoirs provided, and as soon as irreversible heat exchanges are introduced, that efficiency declines.
Why Do Systems Head Toward Equilibrium at All?
There is a danger at this point of falling into the following circular reasoning:
- Closed systems head toward equilibrium because their entropy must increase toward its maximum.
- Entropy increases because heat flows from hotter regions to cooler ones.
- Heat flows from hotter regions to cooler ones because they always head toward equilibrium.
The question we need to answer to get out of this ugly infinite loop is why systems head toward equilibrium at all. Why can't the hotter subsystem get even hotter while the colder subsystem gets even colder? Energy is still conserved in this case, so it doesn't seem to violate any fundamental laws of physics, other than the second law of thermodynamics, which we only derived by assuming that systems do head toward equilibrium.
It's actually a very vexing question, and we will not be able to answer it rigorously in this class, but the general idea is not hard to grasp, and is quite elegant. The crux of the matter lies in the idea of bridging the microscopic goings-on of many particles to the macroscopic quantities we can measure. We first saw this in the kinetic theory of gases (Section 5.5), when we related pressure and temperature to the random motions of particles in a gas.
With a mole of gas containing more than 1023 particles, it's safe to say that we can't account for all of them at once. We therefore need to account for them with some sort of "overview" that can't distinguish between exact situations. An accounting of every gas particle's position and momentum tells us everything there is to know about the physical state of the system, and we call this the microstate of that system. Clearly there are many different microstates that will result in the same average kinetic energy of a particle (which is proportional to the temperature), and these average quantities define what we have called the thermodynamic state, which is also called the macrostate of the system. The following is therefore clear: Every macrostate is associated with many possible microstates which we cannot distinguish from each other because we can't account for the motions of every one of ~1023 particles. Let's do an exercise to see how this view of thermodynamic states leads to the fact that closed systems must evolve toward equilibrium...
We enclose a mole of a gas in a container which includes an airtight barrier that divides it in two. At the beginning, the barrier is in place, and all of the gas is confined to one side of the container. Then the barrier is removed, and the gas is allowed to expand into both chambers for a long period of time, after which the barrier is replaced.
- Clearly waiting a long time allows the gas in the chamber to come to equilibrium before the barrier is replaced. What does this tell us about the amount of gas in each chamber? Is this answer exact?
Most people would claim that there is an equal amount of gas in each chamber, but would then admit that this is an approximation, because it would be folly to assume that a bunch of particles bouncing around randomly are divided exactly in half. We certainly couldn't tell if, in a collection of 1023 particles, there is an imbalance of 2 or 3... Or for that matter, 2 or 3 billion (109), which would still only account for a vanishingly-small percentage discrepancy – the pressure difference, for example, would not be measurable if one side got a billion particles more than the other.
Clearly the key to defining the macrostate is defining the tolerances to which we can measure, and these tolerances will be based on percentages, not absolute numbers. We can see how this works more clearly by talking about situations with numbers we can deal with more easily. From now on, we will need to keep in mind that we assume that individual particles bounce around in a random fashion.
- If we were to attach a tiny flag to one of the gas particles and wait for awhile as it moves around in the chamber, what would be the probability that it would be found on the right side of the chamber?
Given the assumption of "random motion," we are forced to conclude that the probability of finding a specific particle in a specific half of the chamber is 12.
- Suppose there is a total of 10 particles in the entire gas. If we let this gas move through both sides of the chamber for a long time and then replace the barrier, what is the probability that the gas will be divided exactly in half?
Now our discussion takes a mathematical turn. To compute the probability, we need to know how many ways there are to arrange the particles such that they split evenly, and divide that number by all the ways that the particles can split. The numerator is found by computing a combination, which is often stated as "n-choose-r." In this case, this counts the number of unique ways we can select 5 particles out of 10 to place in one side of the container. We will not go into the details of this calculation, but will rather state the result:
n-choose-r=(nr)=n!(n−r)!r!
Plugging in our specific numbers here gives:
10-choose-5=(105)=10!5!5!=252
The total number of ways to arrange the 10 particles is easy to compute. Every particle can go into one of two sides, so for one particle the number is 2. For two particles, the second particle has two choices for each of the first particle's two choices, giving a total of 4. Then the third particle gets two choices for each of the first four, giving 8, and so on. When we reach n particles, there is a total of 2n ways to arrange them. For this example, we therefore get that the probability of seeing the 10 particles split exactly in half is:
P(5:5)=252210=2521024=0.246
There is less than a one-fourth probability that we will see this gas split exactly in half.
- The problem with 10 particles is that we can tell at a glance if they are divided evenly between the two chambers (it doesn’t require any detailed examination to determine this). This is not a fair model for equilibrium, given what we discussed earlier. So let’s include a margin for error. Let’s say that we’ll only recognize that the gas is not in equilibrium if the discrepancy from equilibrium is more than 10%. So for example, our blurry vision allows us to only distinguish distributions that are skewed by more than 60%-40%. So if there are 6 particles on one side of the barrier and 4 on the other, we don’t immediately notice the difference, and we declare the gas “evenly-distributed” in accordance with equilibrium. That is, we define our macrostate to be defined by this 60-40 tolerance. What is the probability we will find the gas in equilibrium under this definition?
Now there are more states that fall under our "roughly half-and-half" requirement than was true in the exact case. We have to account for the 10-choose-4 and 10-choose-6 results now, and add them into the probability calculation:
probability(10particles,10%margin)=P(5:5)+P(6:4)+P(4:6)=(105)1024+(106)1024+(104)1024=0.646
Not surprisingly, the likelihood of seeing an "equilibrium" goes up greatly as our ability to distinguish detail gets worse. But we won't let it get any worse from here. Let's see what happens if we keep this 10% margin for distinguishing microstates but increase the number of particles.
- Using the same 10% margin-of-error definition of equilibrium as we used above, what is the probability of finding a 20-particle gas in equilibrium? Repeat the calculation one more time after doubling the particle number again to 40.
For 20 particles, the 10% margin encompasses distributions of (8:12), (9:11), (10:10), (11:9), and (12:8), giving:
probability(20particles,10%margin)=P(8:12)+P(9:11)+P(10:10)+P(11:9)+P(12:8)=(208)+(209)+(2010)+(2011)+(2012)220=0.737
For 40 particles, the 10% margin encompasses distributions ranging from (16:24) to (24:16). Sparing the reader the math, the result is:
probability(40particles,10%margin)=0.846
Notice that keeping the same percentage margin, the likelihood that we will not be able to distinguish the macrostate from the exact 50-50 distribution gets larger as the number of particles grows. From this example with a very small particle number, it's not difficult to imagine that this probability becomes indistinguishable from 1 when the particle number approaches the enormous number of 1023, even if we make the percentage margin significantly smaller.
So what have we learned here? We found that a macrostate is simply a result of not being able to distinguish microstates, and that the macrostate associated with the equilibrium state (the one where the gas is divided 50-50) includes an absurdly large percentage of all the possible microstates. We state it this way:
The macrostate associated with equilibrium is the one that includes the largest number of microstates.
At last we are in a position to explain why systems head toward equilibrium. Naturally the particles "don't know anything" about what they need to do to get the state to equilibrium, but they don't have to. All they need to do is move randomly, and as they pass through all the possible microstates, eventually the system evolves through the weird, rare microstates and then will spend virtually all of its time in one of the vast majority of microstates associated with equilibrium. From this point on, every time we look at it, it looks the same as before (even though the microscopic state has changed), so we declare it to be at equilibrium.
An analogy might help here. Suppose we have a cookie sheet with 100 pennies on it, all with heads facing up. Clearly this is a highly-ordered state, and the macrostate of "all heads" has only one microstate. Now we rap on the bottom of the cookie sheet, and some pennies randomly flip over. We did not hit it hard, so we can still tell that the pennies are not evenly-distributed between heads and tails, but it is clearly more disordered than before. If we keep hitting the sheet, eventually enough pennies flip between heads and tails that we estimate half of them to be heads and half to be tails. No matter how many more times we hit the sheet from now on, our estimate doesn't change, because the probability that a large number of coins will randomly flip to one variety is very small. In other words, the distribution of heads and tails reaches equilibrium.
We noticed that as we hit the sheet, the state of the pennies became more "disordered," and the equilibrium state was reached when this disorder reached its maximum. In this way, entropy is thought of as a measure of disorder of a system, and the second law of thermodynamics is merely a statement of probability – microstates are far, far more likely to randomly evolve into new microstates that are associated with an equilibrium macrostate than any others. Without getting too technical about how we count the number of microstates using positions and momenta of particles, the entropy of a system's macrostate is defined in terms of the logarithm of the number of microstates available to that macrostate (represented by Ω below, called the system's multiplicity):
S=kBlnΩ
To see that this makes sense, consider the case of two systems at equlibrium being combined into one. If system A has ΩA possible microstates, and system B has ΩB possible microstates, then how many microstates are possible for the combined system? Well, every individual microstate of system A can be combined with every individual microstate of system B to create a new unique microstate for the combined system, so the combined system's total number of available microstates is the product of the multiplicities of the two individual systems:
Ωcombined=ΩA⋅ΩB
Plugging this into the entropy definition above and using the property of the logarithm gives:
Scombined=kBln[ΩA⋅ΩB]=kBln[ΩA]+kBln[ΩB]=SA+SB
This confirms that entropy is an extensive state function with this definition.




