2.2: Force
- Page ID
- 19095
This page is a draft and is under active development.
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Overview
With thermal and bond energies, we could infer changes in the energy of a system through changes in observable properties, the indicators, such as temperature for the change of thermal energy, mass in phase changes, and number of moles in chemical reactions. In the mechanical systems introduced in this chapter, we infer changes in energy by looking at changes in position and speed. Mechanical energies we describe can exchange energy with each other or with the thermal and bond energies. In Chapter 1, we labeled the energy transferred into or out of a physical system due to a difference in temperature between the physical system and its surrounding environment as heat, Q. In this chapter, we introduce another type of energy transfer, which is given the label work, W.
Heat has to do with a temperature difference between two systems, while work has to do with a force applied to a system by another system over some distance. Before discussing work explicitly, we will introduce a basic description of force. We will come back to a more detailed overview of forces in Physics 7B. For right now, we just need a few fairly simple ideas related to force.
Force is a Vector
In general terms, a force is any push or pull between two objects. Variables such as temperature and mass are known as scalars, since there is only a quantity (or magnitude) associated with them, but not direction. Others variables, such as force, velocity, and acceleration, are known as vectors. Vectors have a magnitude (how large is the force?) and direction (which way does the force point?). We will not study vector mathematics in great detail until Physics 7B, but we need to understand the basics in order to understand how energy is transferred through work. Both direction and magnitude affect the amount of energy that one physical system transfers to another physical system. So we need to explore vectors a little bit further. A vector is typically represented by either a bold face, A, or an arrow over the symbol, \(\overrightarrow{A}\).
One way to represent vector quantities is to simply draw an arrow pointing in the direction the vector points (think of the direction of a pull or push for a force), and let the length of the arrow represent the magnitude of the vector (how hard is the push for a force). Shown below are several forces represented in this way with arrows:
Figure 2.2.1: Graphical representation of force vectors.
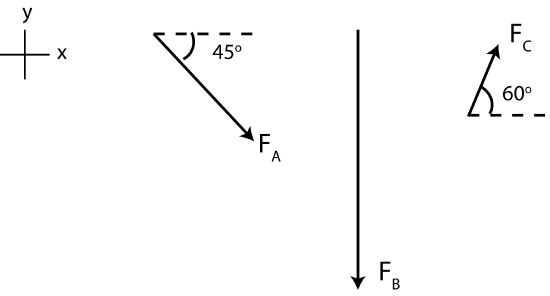
In the above examples, force \(\overrightarrow{F}_A\) points in a direction 45˚ below the +x axis, or we can say it points Southeast. Force \(\overrightarrow{F}_B\) is about twice the magnitude of \(\overrightarrow{F}_A\) since the length of the arrow is double, and it points in the –y direction, or South. Force \(\overrightarrow{F}_C\) is about half the magnitude of \(\overrightarrow{F}_A\) and points in a direction 60˚ above +x axis, or Northeast.
Force is the agent of interactions of TWO OBJECTS
Forces are the agents of interactions between two “objects”. (The quotes around the word “object” signify that it is being used in a general way that includes matter in the form of gases or liquids as well as matter in the solid phase. Sometimes it might even be a single atom or electron. We will omit the quotes from now on, but remember we are using the word object in this more general sense.) Just as there cannot be an interaction involving only one object, there cannot be a force involving only one object.
We normally say, “the force on (name of an object) by (name of another object)” to make clear which two objects are involved in the interaction. For example, we could say, “the force on ball by bat”, or symbolically \(\overrightarrow{F}_{\text{on ball by bat}}\). Generally, a force applied on object A by object B can be expressed in this notation:
\[\overrightarrow{F}_{\text{on A by B}} \]
To realize that this is something you already know and actually does make sense think of the following: use the word “push” in a sentence that refers to you actually pushing. What did you have to say? Did you name an object that you pushed on? Who did the pushing? Can you push without pushing on something? Remember that sometimes it might be something pretty squishy, such as air (which is still a “something,” still an "object"). Can an object be pushed unless there is “something” pushing on it? This is what we mean when we say that force is the agent of an interaction of two objects. There simply cannot be an interaction without there being two objects. And there cannot be a force without there being two objects.
Two Types of Force
Let us consider the example of the force on ball by bat. Does the force by the bat continue to act on the ball after the bat is no longer touching the ball, or does the force act only while the ball and bat are in contact? Recall that force is an agent of interaction, so another way to ask the question is whether the ball and bat continue to interact after they are no longer in contact. The answer is they interact only while in contact. Thus, the force the bat exerts on the ball (and, likewise, the force that the ball exerts on the bat) acts only while the two objects are in contact. Consequently, we call this type of force a contact force.
Some forces act even when the objects are not touching, some even when extreme distances separate the objects, and these are referred to as long-range forces. Think about the force of gravity. The Earth pulls down on all objects near its surface. Note that we have two objects: the Earth and the object being pulled down. We know from everyday experience that the gravitational force of the Earth on an object is present whether the object is touching the Earth or not. Apparently the interaction between the Earth and a nearby object is unlike the force between the bat and the ball. The interaction and the force, the agent of the interaction, continue to exist even when there is no direct contact. The gravitational force is a long-range force. The force of gravity between our sun and each the planets in our solar system does indeed get weaker as the distance between the sun and the particular planet increases, but it is definitely still there. The gravitational force is truly long-range.
There are also non-contact forces that act between objects that are not touching, but “die off” or “go to zero” as soon as the objects get more than a little distance apart. Most of the forces that hold atoms together into molecules and hold the particles of solids and liquids together are like this. The interaction and the agent of the interaction, the force, exists, even though the particles are not touching, but the force decreases to zero in magnitude pretty fast as the particles begin to separate just a little bit from each other. We will see examples of this behavior in Chapter 3 when we study the forces between neutral atoms or molecules. Sometimes this kind of force is said to be a short-range force.
Balanced and Unbalanced Forces
There is one last important idea that we will need to use, but is also part of our common experience with pushes and pulls. We can easily imagine two people pushing on a table from opposite sides. If person A pushes harder than person B, the table moves. If both people push with the same strength but in opposite directions, the table does not move. In the first case, we say the forces applied on the table (one object) by the two objects (the two persons) were unbalanced, and as a result, the table moved. In the second case, the two objects applied equal and opposite forces on the table and the table did not move. We say the forces applied by the two persons were balanced. The figure below provides a few examples of balanced and unbalanced forces on an object using the graphical representation of a vector.
Figure 2.2.1: Graphical representation of balanced and unbalanced forces
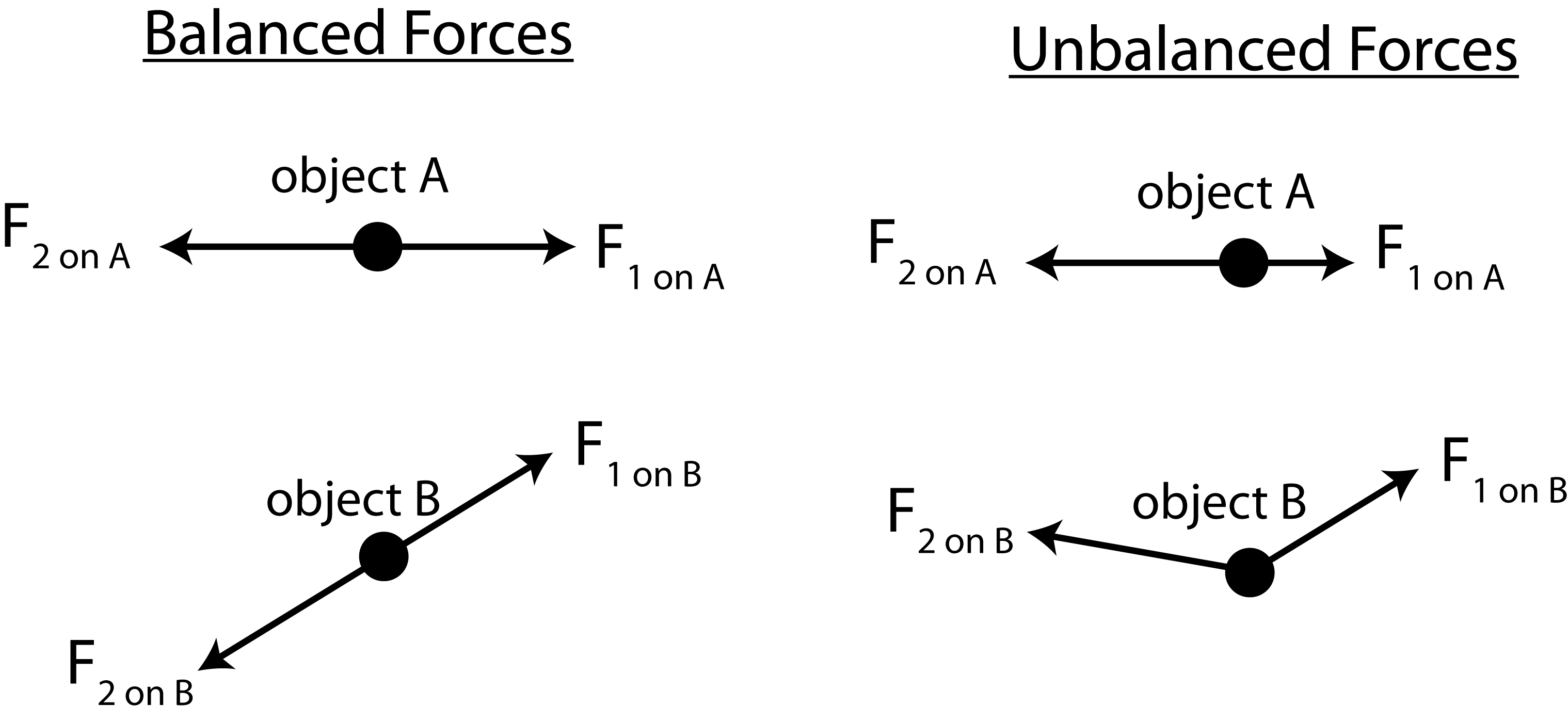
Note, you can have forces of the same magnitudes but still be unbalanced. Picture a scenario of two people pushing a table with the same strength and in the same direction, the table will clearly move. For the unbalanced forces in the figure above, can you guess which direction the object will move? The reason it is important to consider the total force acting on an object, is that it is precisely the total force that matters when considering the work done on our object. Once we know the total force, we will be able to calculate work and figure out how the energy of the object changes due to this total force.


