2.3: Work
- Page ID
- 19096
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Definition of Work
Work, \(W\), is a transfer of energy from one physical system to another via a force acting between the two through a distance. Only the part of the force that acts parallel to the displacement contributes to work. The general algebraic expression for work done along a path \(s\) from point A to B is:
The "\(\cdot\)", known as the dot product, in the equation above means that only the component of force that is parallel to the path contributes to work. When the force is constant along some displacement, \(\Delta x\), Equation \(\ref{workDef.int}\) simplifies to:
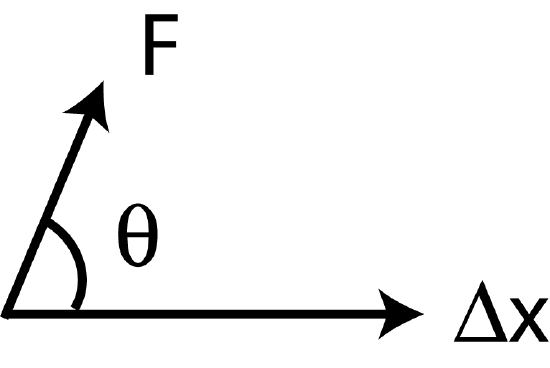
\[ W = | \overrightarrow{F}|| \overrightarrow{\Delta x} |\cos\theta\]
where \( |\overrightarrow{F}|\) is the magnitude of the force, \( |\overrightarrow{\Delta x}| \) is magnitude the displacement vector, and \(\theta\) is the angle between these two vectors as shown in the figure below. The term, \(|\overrightarrow{F}|\cos\theta\), determines the amount of the force that points in the direction of displacement.
Figure 2.3.1: Force and displacement resulting in work.
When Does Work Happen?
In order to accomplish work on an object there must be a net force applied on the object, and the object must move in the direction of the net force. If either of those conditions are not met, then there is no work. For example, if an object is traveling freely with no forces acting on it (such as a comet moving at constant speed in outer space far from other objects), there is no work being done on the object despite it moving through a distance. The reverse is also true: if an object has forces acting on it, but is not moving (as in the example of two people pushing on a table with equal but opposite forces), there is also no work being done on the table. What matters is the net force, not the individual ones. There is one last way for no work to be done. Imagine someone carrying a weight across a room while walking at a constant speed. Your intuition may be tempted to tell you that there is a force being exerted through a distance, and therefore work is being done, but as is often the case in physics, your intuition would be wrong! The force you exert while carrying an object is entirely up, but the displacement while walking is completely horizontal. The best way to improve your intuition about work is to work through examples, apply the definition, and see where it leads you.
Like heat, work is a scalar (i.e., has no direction associated with it) and is measured in the SI unit of energy, joules. A joule is equivalent to a newton·meter, or J = N·m, since a newton is the SI unit of force.
Consider a box being pushed horizontally along a frictionless surface as shown in the figure below.
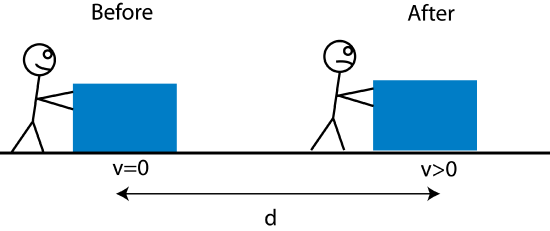
The person exerts a force on the box, and we observe the box moving with an increasing speed along the surface. This force results in work being done on the box, since the force is in the same direction as the displacement d, and there are no other horizontal forces acting on the box. The work being done implies that the energy of the box must be increasing. From Equation 1.2.1, we obtain \(\Delta E_{tot}=W\). The next question we want to ask is what type of energy is changing? The physical property we observe increasing is the speed of the box. The energy associated with speed of objects is known as kinetic energy, KE, where speed is its indicator.
In another example, a person lifts a ball vertically.

In this example we assume that the speed of the ball is zero before and after it is lifted. The person does work on the ball, since a force by the hand on the ball is exerted in the same direction as the displacement d on the ball. Thus, the energy of the ball must have increased in this interval. What type of energy is this? The only physical characteristic of the ball that changed is its height, since the speed remained at zero. The energy associated with height is known as gravitational potential energy, PEg, where height is its indicator.
Another system we will study intensively in this course is the spring-mass system. In the figure below a mass attached to a spring (spring-mass system) is mounted to a wall. When there is no force acting on the spring-mass ("before" in the figure), we say that the spring-mass system is in its equilibrium position. In the particular interval shown in the figure, a horizontal force is applied on the spring-mass displacing the spring-mass by a distance d from equilibrium.
Again, we assume that the speed of the mass remained zero, while the person holds the mass in place when stretched. Work is being done since the force, \( \overrightarrow{F}\), is in the same direction as the displacement d. The physical characteristic that changes in this particular interval is the displacement from equilibrium of the spring-mass system. We call the energy associated with this change, the spring-mass potential energy, PEsm, where displacement from equilibrium is its indicator.
Note, the indicators for both potential energies introduced here, PEg and PEsm, depend on the position of the physical system. We will look at these three energies in greater detail in the coming sections.



