11.2: Electric Force

Last updated
Save as PDF

Page ID: 78802

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Electric Charge

Electric charges are measured in Coulombs, abbreviated C. The fundamental charge, \(e\) is given by:

\[e\equiv 1.602 \times 10^{−19} \text{ C}\]

The electron, \(e^{-}\), has a charge of \(q=-e=-1.6\times 10^{-19}\;\text{C}\). The proton, \(p^{+}\), has a charge with the same magnitude but it's positive, \(q=+e=1.6\times 10^{-19}\;\text{C}\). All atoms, molecules, or charged macroscopic objects get their charge from either an excess or deficit of electrons compared to the number of protons they have: a charge of "e" is thus considered fundamental, as all observed particles or objects with charge have some integer multiple of this value. For example, if a macroscopic object has an excess of \(6.24\times 10^{19}\) electrons, then that object has a charge of -10 C.

Electric charge is conserved, it cannot be created out of thin air or disappear forever. For example, when you charge an object by rubbing it with a cloth, then the amount of charge that you add (or remove) to the object is the amount of charge that gets removed (added) from the cloth. The way charges get transferred between objects highly depends on the physical properties of those objects. Two distinct categories are conductors, objects where charges are free to move, and insulators, objects where charge is locked in place.

Electric Force

An electric force is an interaction between two electric charges. It is one of the fundamental forces in nature, which we will later combine with magnetism to describe the electromagnetic force. The force depends on the sign of the charges, the magnitude of the charges, and the distance between them. The figure below shows forces for the three possible pair combinations of charges, emphasizing that the electric force, like all other forces, is a pairwise interaction.

Figure 11.2.1: Forces Between Charges

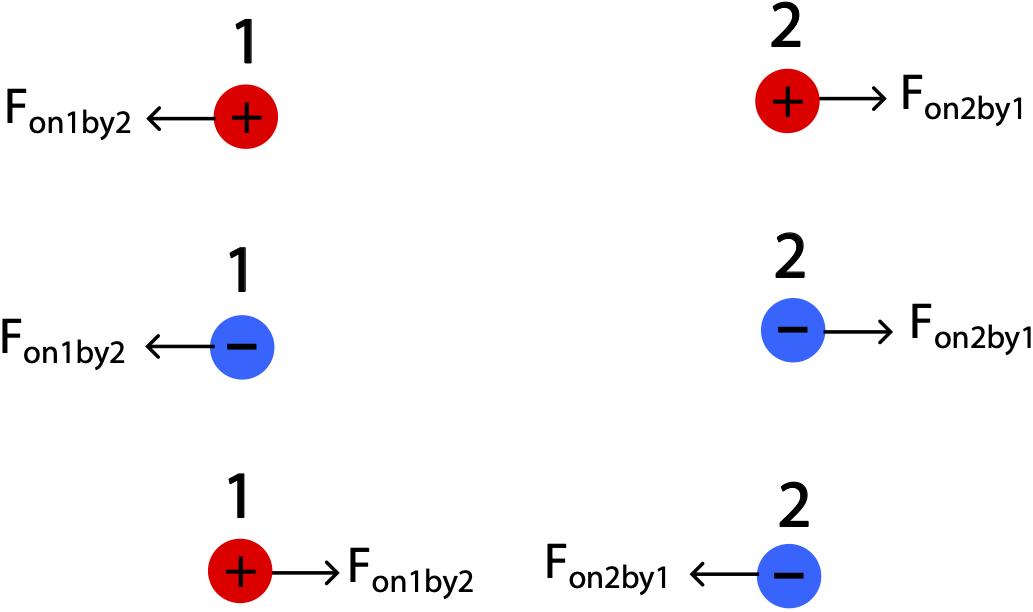
The forces are governed by Newton's third law, such that the force of charge 1 by charge 2 is equal in magnitude but opposite in direction to the force on charge 2 by charge 1. We see from the figure that when both charges are the same, the force wants to push them apart. When the two charges have opposite sign, the electric force wants to bring them together. This is a fundamental property of the electric force: like charges repel and opposite charges attract.

The magnitude of the electric force between two charges \(q_1\) and \(q_2\), with their centers separated by a distance \(r\), is given by the following equation:

\[F_{\text{on}q_1\text{by}q_2}= \Big|\dfrac{kq_1q_2}{r^2}\Big|;\; k=9 \times10^9 \dfrac{\text{ Nm}^2}{\text{C}^2}\]

The constant \(k\) converts force to the proper units of Newtons. The force increases linearly with the magnitude of each charge, but decreases as the inverse of the distance squared. Thus, the force become weak quickly as the charges separate. Newton's third law guarantees that the force exerted on \(q_2\) by \(q_1\) has the same magnitude as the force above but will point in the opposite direction.

The absolute value is placed there to insure that we are calculating the magnitude of the force regardless of the signs of the charges. However, force is a vector, so we also need to consider the direction of the force. Let is distinguish the two interacting charges, as one being the charge that generates the force, the source charge. The other charge that feels the force is the test charge. We then define a vector that points radially (along the distance separating the two charges) away form the source charge at the location of the test charge. The vector that specifies the direction is \(\hat{r}\), where the "hat" above the "r", means it is a unit vector, which has no magnitude (and thus no units). It is a vector that specifically specifies the direction away from the source charge.

Figure 11.2.1: Direction of Electric Force

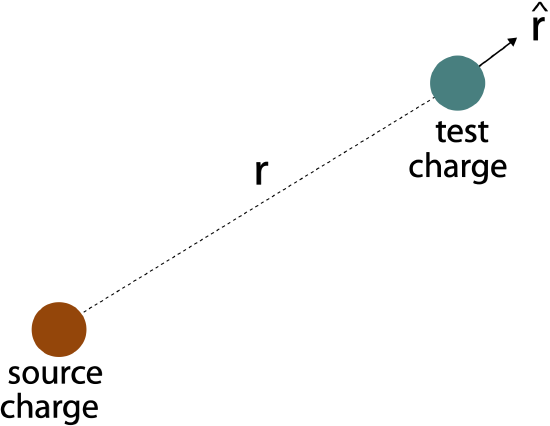
We then write down the force vector in the following way, known as Coulomb's Law, which describes an interaction between point charges:

\[\vec F_{\text{on} q_1 \text{by} q_2}=\dfrac{kq_1q_2}{r^2}\hat r\]

Let us now check that this equation is consistent with properties of interacting charges. From the above equation you can see that whether both \(q_1\) and \(q_2\) are both positive or both negative, the quantity \(q_1q_2\) will be positive, so the force vector points along the radial unit vector. Thus, the force points away from the source charge. This force is then repulsive, since the two charges repel each other. When the two charges have opposite signs, then the quantity \(q_1q_2\) is a negative, so the force vector points in the opposite direction of the radial unit vector (toward the source charge). Therefore, the two charges are drawn toward each other, and the force is attractive.