6.1: Background Material
( \newcommand{\kernel}{\mathrm{null}\,}\)
Text References
Using Parallax
One of the challenges for today's lab is determining how far away an image is from the viewer. We already know that things look larger when they are closer, and smaller when they are far away. But when light is reflected or refracted on its way from the object to the viewer, the size of the image seen is affected, so we can't rely on this.
While there is no way to determine an image's distance from us without knowing its actual and apparent size, and the path that the light had to follow to get to us, there is nevertheless a way to compare the relative distances of two images, using something called parallax. Consider viewing two images aligned with one another, with one being farther away than the other. We can determine which one is closer simply by changing the angle of perspective so that they are no longer aligned.
Figure 6.1.1 Changing Perspective to Exploit Parallax
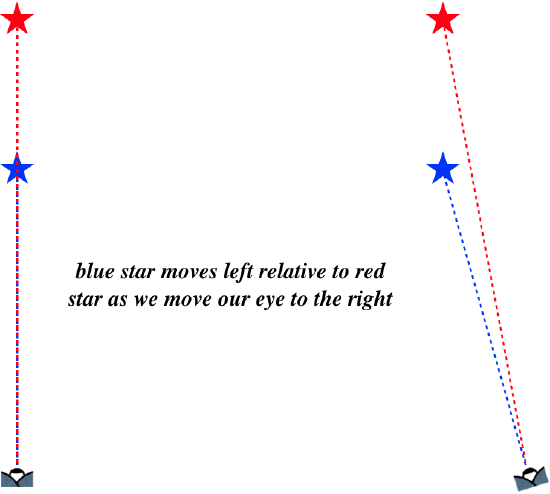
As we change our eye position, the change in relative positions of the images reveals which is closer – it moves in the opposite direction as our eye relative to the other object. So how can we use this to locate an image when the light follows a reflected or refracted path? We compare position of an image from the altered path with a "reference" image that comes from an unaltered path. Let's look at a simple example with a plane mirror.
Start by placing a vertical rod in front of a vertical plane mirror, such that when we look in the mirror, the top of the rod's reflection reaches the upper edge of the mirror. Next place another rod behind the mirror so that its top extends beyond the top of the mirror. If the two rods are placed such that the line joining them is perpendicular to the plane of the mirror, then looking straight into the mirror (along the line joining the rods) will give the appearance that the image of the rod in the mirror is continued by the image of the rod above the mirror.
Now what do we we see if we move our eye right or left? If the rod placed behind the mirror happens to be at the same place as the image of the rod in front of the mirror, then they remain aligned at the top of the mirror – parallax does not cause one to move side-to-side differently from the other. But if the rod we see above the mirror and the image in the mirror move relative to each other, then we know that the rod behind the mirror is not the same distance away as the image in the mirror, and we can tell which one is closer by the relative directions that they move (the closer one moves the opposite direction as our eye motion).
Figure 6.1.2 Reflection and Rod Behind Mirror the Same Distance Away

Figure 6.1.3 Reflection Closer than Rod Behind Mirror

Figure 6.1.4 Reflection Farther than Rod Behind Mirror

We know from our studies of geometrical optics how to find where an image is if we know where the object is, and the sort of path the light has to follow, but this parallax trick gives us a way to experimentally determine this. We just move the rod behind the mirror until it remains aligned with the reflection, and wherever we move this rod to is the location of the image. We make adjustments to the position of the "test rod" by noting that if it moves the same way relative to the reflection as our eye moves, then it is too far, and it is too close if it moves the other way relative to the reflection.
Snell's Law Without a Laser
It is likely that we have seen visual evidence of refraction of light when goes from one region to another with a different index of refraction, using lasers. But this phenomenon has been understood in its present state for over 1000 years (first explained by a Persian scientist, with Snell eventually getting credit for work he did around 1600), and certainly none of them had lasers to work with. To be clear, we are talking again about confirming this law experimentally – the various mathematical proofs (like the one using Huygens's Principle) are not what we are talking about here.
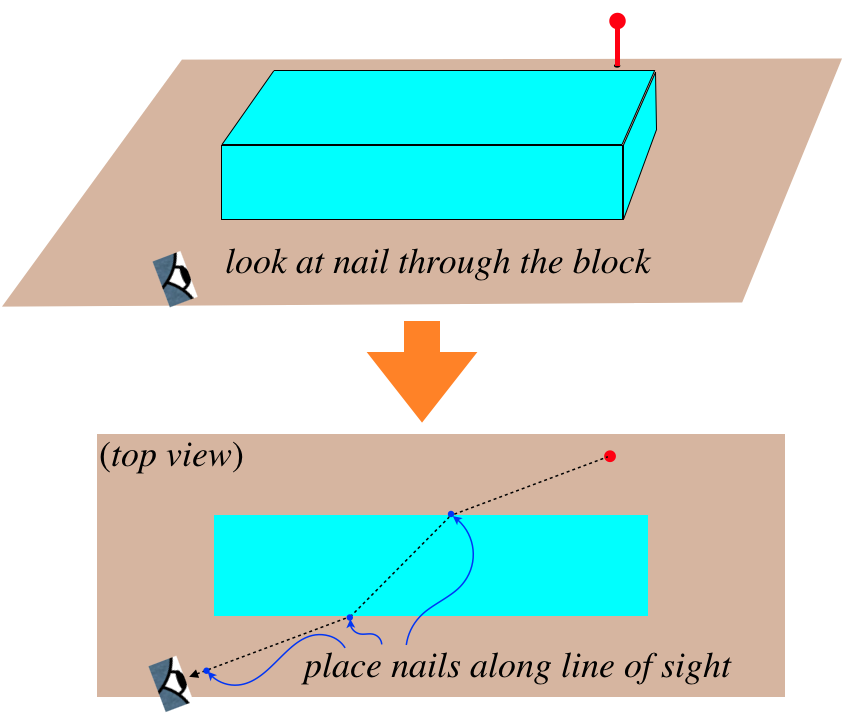
Given that we cannot see rays like we do laser beams, we need to somehow define them another way. Naturally two points define a line, so if we position our eye so that two vertical rods are aligned, then we can be sure that the ray that enters our eye is the one that passes through both of them. If we add more such rods in alignment, the ray passes through all of them on its way to our eye.
In our experiment we will be using a rectangular prism of some unknown transparent substance, and we can trace the path of a light ray from a nail to the prism, then from the other side of the prism to our eye by placing nails in line with our sight of the original nail.
Figure 6.1.5 Using Nails to Trace a Ray