1.5: Standing Waves
( \newcommand{\kernel}{\mathrm{null}\,}\)
Interference Patterns
We found that interference occurs between two identical waves, but we didn't mention what the source of two identical waves might be. We will find that most of the time the two waves are actually the same wave, where one part of it has been diverted somehow, so that it behaves like a separate wave. When we witness the interference created in such a situation, it is often in the form of an interference pattern. This is a recognizable pattern of intensity that repeats itself in space or in time, or in both. We will see lots of these patterns in the sections to come, but as usual we will start with a simple (but important) one-dimensional example of an interference pattern, called a standing wave. [Actually, standing waves occur in 2 and 3 dimensions as well, though we will confine our discussion to those of the 1-dimensional variety.]
Alert
The moniker "standing wave" puts yet another strain on our definition of what it means to be a wave. It does satisfy the wave equation (as does any superposition of waves), but although the wave equation yields a wave velocity, this waveform does not propagate at all. It is better to think of standing waves as what they are – interference patterns.
All interference patterns are formed from multiple identical waves, and like so many other interference patterns, this is accomplished through multiple versions of the same wave. In the case of the standing wave, these two versions are the result of wave reflections off two endpoints. That is, a single wave bounces back-and forth between two endpoints, and as it crosses itself during the journey, the standing wave interference pattern is formed from the superposition – the two waves that are interfering only differ in their directions of motion.
Wave Reflection & Transmission
Before we delve into the details of standing waves, we first need to look at the phenomenon that makes them possible – wave reflection. The mathematics of wave reflection can become quite involved and we will not delve into it here, but the bottom line is that waves reflect off sudden changes in the medium. We have found that the medium is best characterized by the speed of waves that pass through it, and in fact it is correct to say that a wave reflects when it encounters a region of the medium where the wave speed changes.
At this point one might ask why the wave doesn't simply continue in the direction it was going, but at a different speed. It does! But it also reflects. That is, the wave splits into two parts, called the reflected wave and the transmitted wave. Of course, energy is conserved during this schism, so the energy in the original wave is greater than the energies in either of these waves. The amount of energy that goes to each wave is determined mathematically by a process known as "matching boundary conditions" at the point of reflection, but as mentioned earlier, we will not make a close examination of this process here (this topic is explored in courses on quantum mechanics, such as Physics 9D).
The requirement that the speed of the wave changes at the point of reflection in the medium doesn't distinguish between the wave is coming from a faster medium to a slower one, or from a slower one to a faster one. It turns out that the wave will partially transmit and partially reflect, no matter which direction it is going. But there is an observable phenomenon that distinguishes these two possibilities. Suppose a pulse of a wave on a string consists of just a single bump (like half a sine function) that lies on the top half of the string. If this wave reaches a point in the medium where it speeds up (the string's linear density goes down), then the reflected pulse remains in the top half of the string. But if the pulse encounters a point in the medium where it slows down (the string's linear density goes up), then the reflected pulse flips to the bottom half of the string. The transmitted wave never flips over.
Figure 1.5.1 – Reflection and Transmission (Slow-to-Fast Medium)

Figure 1.5.2 – Reflection and Transmission (Fast-to-Slow Medium)
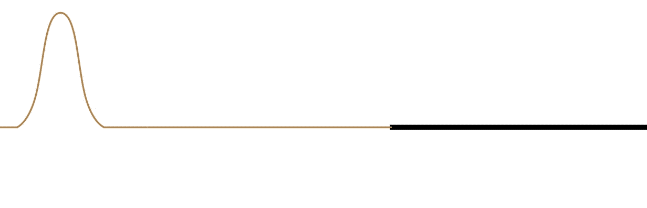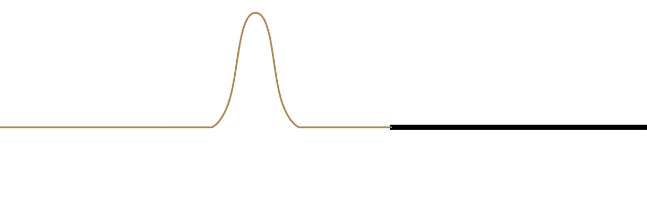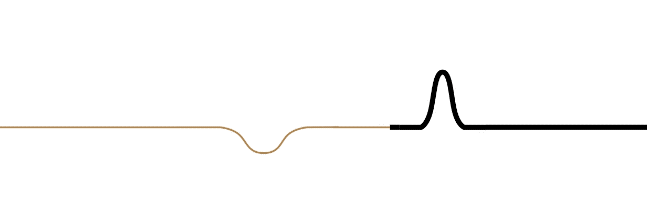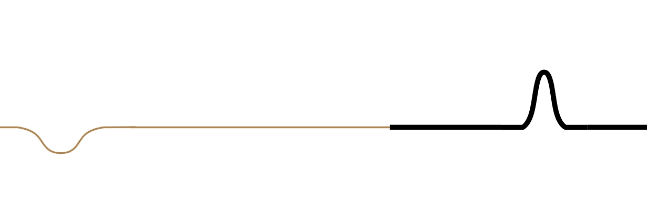
It should also be noted that the reflected wave in both cases reflects its wave form along -x\leftrightarrow +x. This is not obvious in the case of a symmetric pulse, but if the wave is asymmetric, then it becomes apparent.
Figure 1.5.3 – Reflection of an Asymmetric Wave (Fast-to-Slow Medium)
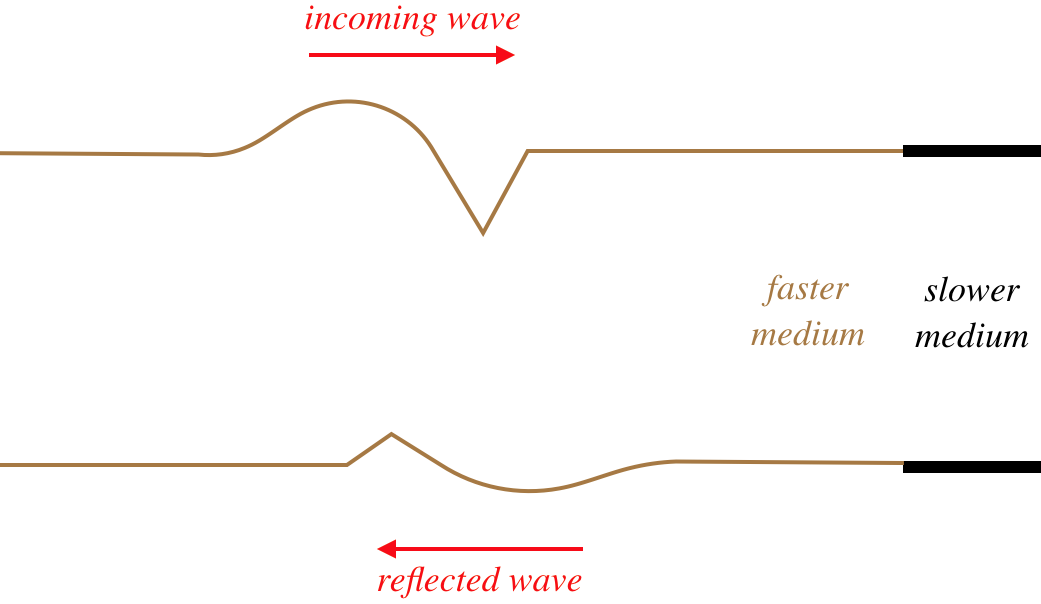
The leading edge of the incoming waveform is the leading edge of the reflected waveform. While there is some loss of amplitude for the reflected wave compared to its incoming counterpart (some of the energy is taken by the transmitted wave), the wavelength of the reflected wave is the same as the incoming wave. This is because the velocity of the reflected wave is the same as the incoming wave. The wavelength of the transmitted wave will not match the wavelength of the incoming wave, however. The time span between the front and rear of the waveform striking the new medium is the same time as it takes for the full waveform to be transmitted, so the periods of the incoming, transmitted, and reflected waves are all the same, but since the velocity is different for the reflected and transmitted waves, the result is different wavelengths for these waves (\lambda will be longer in the faster medium).
Reflection without Transmission
In order to discuss standing waves, we need to completely confine the wave between two endpoints – no energy can be allowed to escape via transmission. We can make such a confinement simply by cutting off the medium at the endpoints. The wave will reflect off this sudden absence of medium, and all of the energy of the incoming wave returns in the reflected wave. But does the wave flip over or stay upright in such a case?
In fact both of these results are possible, because the edge of the medium can react in one of two ways. If the edge of the medium is held fixed (i.e. not allowed to exhibit the displacement that the wave provides every other point in the medium), then the reflected wave flips over. If the edge of the medium is free to displace, then the reflected wave does not flip over.
Figure 1.5.4 – Reflection off a Fixed End
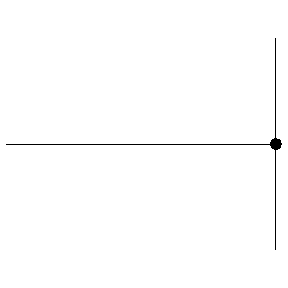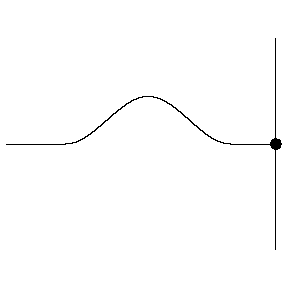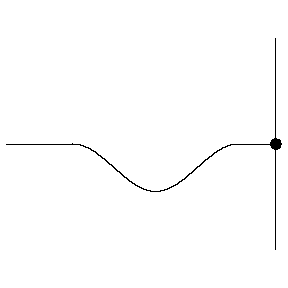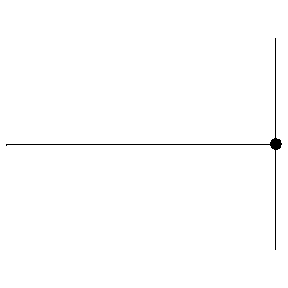
Figure 1.5.5 – Reflection off a Free End
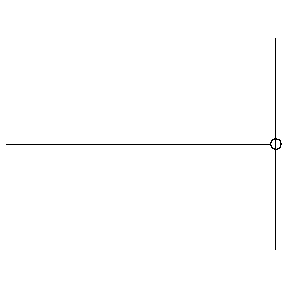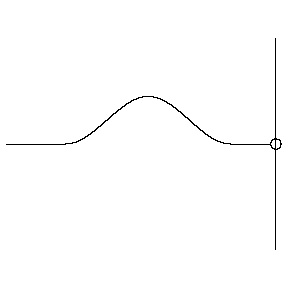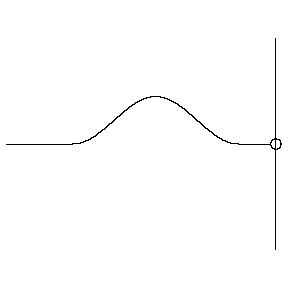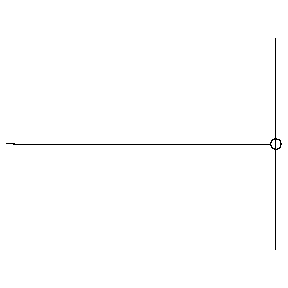
Explaining this result is quite tricky from a perspective of forces on the end of string, and even after figuring that out, it's hard to extend it to other types of waves (this phenomenon applies to all waves, though sometimes determining what is meant by "fixed" and "free" can be tricky). But there is a nice way to use an imaginary model to achieve this result. It goes like this:
Suppose we model a single wave hitting the end of the medium with two waves, moving in opposite directions through the point that is the end of the medium and passing each other. Clearly the second wave doesn't exist, since there is no medium beyond the end, but its emergence from the passing point is seen as the "reflected wave," while the other wave vanishes past the passing point. With this model, we first see that they must have the same basic waveform, and that the leading edge of one wave must correspond to the leading edge of the other. But now we ask how the imaginary wave (i.e. the second wave, before it emerges as the reflected wave) must be oriented for the passing point to be fixed or free. For the passing point to remain stationary, the superposition of the two waves at that point must result in total destructive interference. This can only happen if the second wave is inverted compared to the first wave, so when it emerges as the reflected wave, it has been flipped over. If the passing point moves freely, the two waves cannot interfere destructively, so the second wave emerges upright. Note that this analysis tells us that the free end displaces an amount equal to twice the amplitude, since the waves are identical and the interference is constructive.
As often as we use harmonic waves, it is useful to put the phenomenon of reflected waves in that context. When we flip over a sine or cosine wave, the result is identical to shifting that wave by a phase of \pi:
flip\;wave\;function:\;\;\;A\cos\left(\frac{2\pi}{\lambda}x\pm\frac{2\pi}{T}t+\phi\right)\;\rightarrow\; -A\cos\left(\frac{2\pi}{\lambda}x\pm\frac{2\pi}{T}t+\phi\right)=A\cos\left(\frac{2\pi}{\lambda}x\pm\frac{2\pi}{T}t+\phi+\pi\right)
The inversion of a reflected wave after coming off a fixed end or a slower medium is therefore often referred to as a phase shift of \pi.
Standing Wave Mathematics
Now we know that we can get a wave to bounce back-and-forth between two ends of a medium, and the waves going each way are identical. If conditions for these waves are just right, their superposition results in a standing wave.
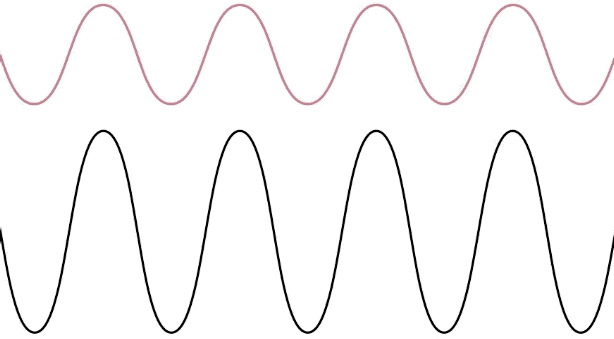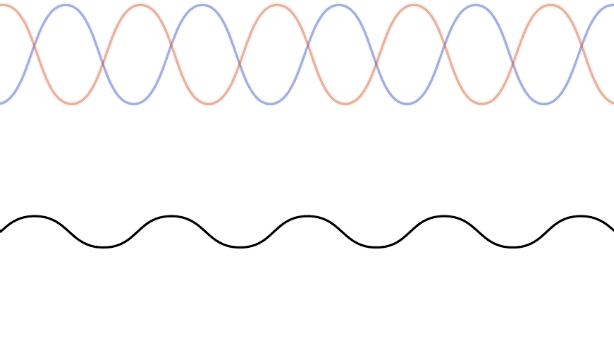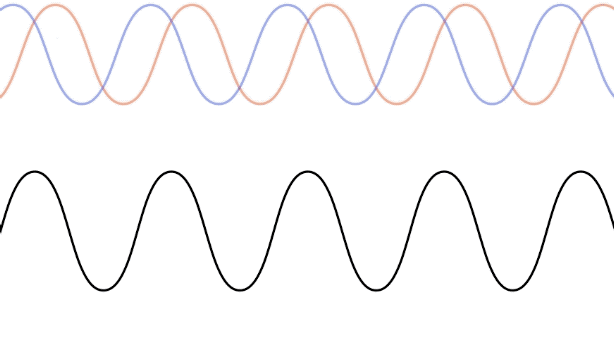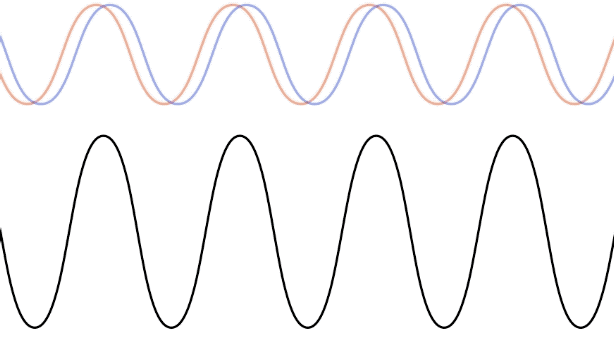
Let's see how this result occurs mathematically. This requires superposing two wave functions with the wave wavelength (wave number) and period (angular frequency) that are moving in opposite directions:
\begin{array}{l} right-moving\;wave:&&f_1\left(x,t\right)=A\cos\left(kx-\omega t+\phi_1\right) \\ left-moving\;wave:&&f_2\left(x,t\right)=A\cos\left(kx+\omega t+\phi_2\right) \end{array}
Recall that this standing wave occurs because a single wave is bouncing back-and-forth between endpoints in the medium. The endpoints must either each be free (no phase shift) or fixed (\pi phase shift). For the sake of getting an easy-to-read result, we'll assume that a fixed endpoint lies at position x=0. Because we are talking about a position where the wave reflects, and because the point is fixed, the two waves must be out of phase by \pi radians. Mathematically this means that the difference in their phase constants is \pi:
\phi_2-\phi_1=\pi
Plugging x=0 and \phi_2=\phi_1+\pi into the superposition of the two waves and setting the result equal to zero (that point remains fixed by our simplifying assumption), we get:
0=f_{tot}\left(0,t\right) = A\cos\left(0-\omega t+\phi_1\right) + A\cos\left(0+\omega t+\phi_1 + \pi\right)=A\cos\left(-\omega t+\phi_1\right) - A\cos\left(\omega t+\phi_1\right)\;\;\;\Rightarrow\;\;\;\cos\left(-\omega t+\phi_1\right)=\cos\left(\omega t+\phi_1\right)
We can solve this for \phi_1, which comes out to be: 0, \pm 2\pi\, \pm 4\pi\dots. We'll take the simplest solution of zero, which leaves us with the following wave function:
f_{tot}\left(x,t\right)=A\cos\left(kx-\omega t\right) - A\cos\left(kx+\omega t\right)
We can now apply the following trigonometric identity to get a simplified form of the standing wave function:
\cos\left(X-Y\right)-\cos\left(X+Y\right)=2\sin X \sin Y \;\;\;\Rightarrow\;\;\; f_{SW}\left(x,t\right)=2A\sin kx\sin\omega t = 2A\sin \left(\dfrac{2\pi x}{\lambda}\right) \sin\left(\dfrac{2\pi t}{T}\right)
All harmonic waves are collections of harmonically-oscillating points in a medium, that vary in total phase from one position to the next. Traveling waves satisfy this, but the amplitudes of these oscillators are all the same in this case. When interference occurs, the amplitude can vary from one position to the next as well (e.g. positions of destructive interference have zero amplitude, and positions of constructive interference have very large amplitudes), and this is evident in this result for the interference pattern we call a standing wave. This formula can be written as a collection of harmonic oscillators all with the same a period (and therefore the same sine function), but with different amplitudes at different positions:
It is not hard to visualize this wave – it is a sine function along the x-axis, which remains in place ("standing") as its displacement at various positions oscillates with time. That is, it is exactly like the standing wave depicted in Figure 1.5.6, with the left end being the origin. There are several things to note about this standing wave:
- There are fixed points that occur at specific positions on the standing wave (when the sine function of position vanishes), called nodes. These are separated by a distance equal to one half the wavelength of the traveling waves. We will say that the "wavelength" of the standing wave equals the wavelength of the traveling waves that are forming it.
- The maximum displacement of the standing wave only occurs at specific positions, called antinodes, which are also separated by a distance of one half wavelength.
- The maximum displacement of the standing wave (2A) occurs when the sine functions of time and position both equal 1, and it is twice the amplitude of the traveling waves that compose it. This is referred to as the "amplitude" of the standing wave.
- The period of oscillation of the standing wave (the time it takes to get back to where it started) is the same as the period of the traveling waves that compose it (T).
- This one-dimensional function cannot be written in the form f\left(x\pm vt\right), but it is a solution of the wave equation. The reason is that the ambiguity of the sign of \pm v is washed away in the square of v in the wave equation. We originally described a wave as a phenomenon that transports energy from one position to another, and a standing wave clearly does not do this, so it is probably better described as a special time-varying interference pattern.
Note that we could have insisted that the end of the medium at the origin is free rather than fixed. This would result in no phase shift for the reflected wave, and it is left as an exercise to show that this results in a standing wave function with two cosine functions replacing the two sine functions in Equation 1.5.7.
Standing Wave Harmonics
The formula for a standing wave is still rather abstract, in that it really only restricts the behavior of the standing wave at a single point (the origin), and assumes that we know the wavelength and period. Here we will consider a different restriction, one that is more useful for physics applications. We will define a distance between two endpoints, and insist that a standing wave forms between them. We also need to specify if the ends are held fixed or are free. If an end is fixed, it must be a node of the standing wave, and if it is free, it must be an antinode, so this greatly restricts the standing waves that can be formed. In particular, it puts very specific restrictions on the possible wavelengths a standing wave can have.
Let's start with the longest possible wavelength that a standing wave can have if its two ends are separated by a distance L. There are three possibilities in terms of the node/antinode endpoints: Both ends can be fixed (nodes), both ends can be free (antinodes), or there can be one of each type at the two ends. Note that in the first two cases, the distance between the two ends must equal one-half wavelength, while in the third case the distance between the ends is one-quarter wavelength (again, we are looking specifically at the longest possible wavelengths to satisfy these conditions).
Figure 1.5.7 – Longest Wavelength Standing Wave – Both Ends Fixed
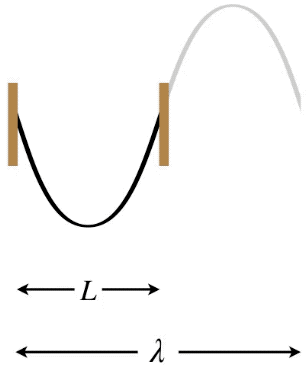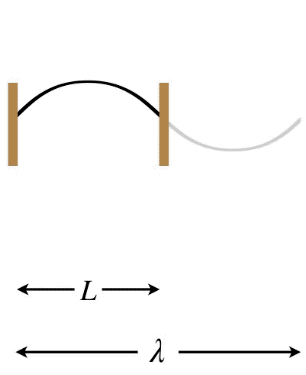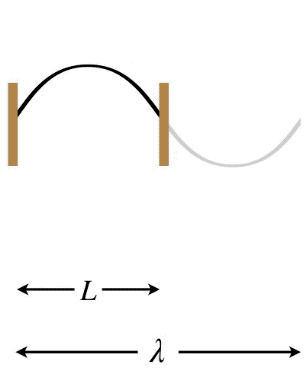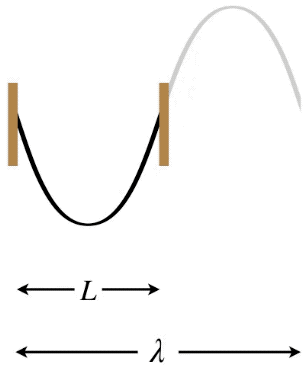
Figure 1.5.8 – Longest Wavelength Standing Wave – Both Ends Free
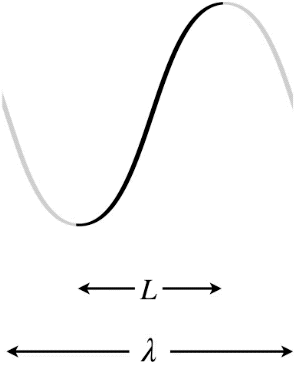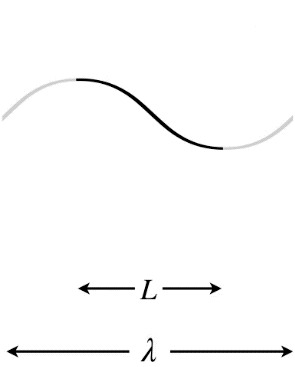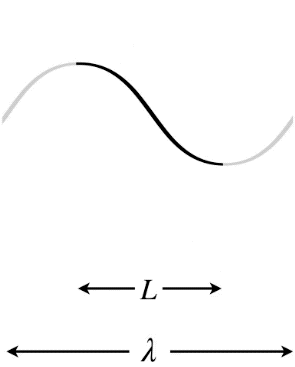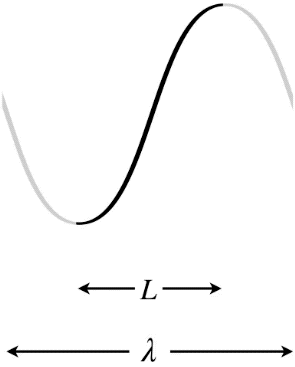
Figure 1.5.9 – Longest Wavelength Standing Wave – One End Free, One End Fixed

In the Figures above, the dark curves indicate the extent of the medium (i.e. that which is actually vibrating). The gray portions are only added to show the actual wavelength \lambda of the standing wave and how it relates to the length L of the medium.
These are not the only standing waves possible for the given length L. An infinitude of additional standing waves are possible with shorter wavelengths as well, but only certain wavelengths will work. We can characterize these by the number of nodes or antinodes present. The set of standing waves allowed for a given length of medium are called the harmonics of the system. The harmonic with the longest possible wavelength is called the fundamental harmonic, and the rest are numbered up from there according to frequency.
Speaking of frequency, it must be noted that the frequency of oscillation of a standing wave changes from one harmonic to the next. As we have already seen, the wavelength of the standing wave equals the wavelength of the the two opposite-moving traveling waves, and the period (or frequency) of the standing wave matches the traveling wave periods as well. If we consider a shorter-wavelength standing wave (one with more antinodes), then the wavelength of the traveling waves that make it must also be shorter. But the medium is unchanged, so the speed of those traveling waves must remain the same. This can only be true if the frequency of the traveling wave has gone up, which means the frequency of the standing wave must also go up.
We define the n^{th} harmonic as that harmonic with a frequency that is n times as great as the fundamental harmonic. Let's see what that means for the three possible endpoint conditions. We'll start with both ends fixed. For the fundamental harmonic, we found that the wavelength was double the length of the medium. The next shortest wavelength would include a single node between the two endpoints, and as allowable standing waves get shorter and shorter, we simply keep adding nodes, one at a time (this can be described as fitting an additional half-wavelength between the endpoints each time).
Figure 1.5.10 – Harmonics, Both Ends Fixed
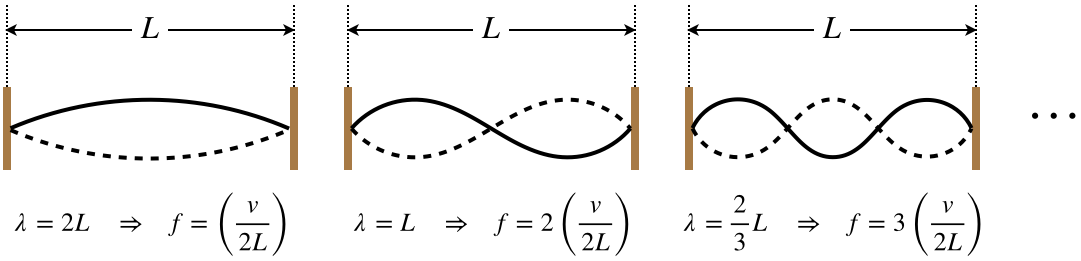
The pattern for this case is clear: The n^{th} possible standing wave has a frequency of n times the fundamental harmonic, which means that the each time we add an antinode, we get the next-highest harmonic, and the number of antinodes equals the order of the harmonic. Mathematically we summarize it this way (v is the speed of the traveling wave on the string):
\lambda_n = \dfrac{2L}{n}\;\;\;\Rightarrow\;\;\; f_n=n\left(\dfrac{v}{2L}\right)\;,\;\;\;\;\;n=1,\;2,\;3,\;\dots
If we look at both ends free, we find that the same pattern emerges, which should be clear from the fact that the wavelength of the fundamental harmonic is the same when both ends are free or fixed. The only difference between the two cases are that we count the number of nodes to get the harmonic in the both ends free case, not antinodes, as we did for the case of both ends fixed.
When only one end is free, we get a different result when it comes to counting harmonics. We still squeeze additional half wavelength between the endpoints for the next possible wave, but the frequencies of the harmonics have a different relationship to the fundamental.
Figure 1.5.11 – Harmonics, One End Fixed, One End Free
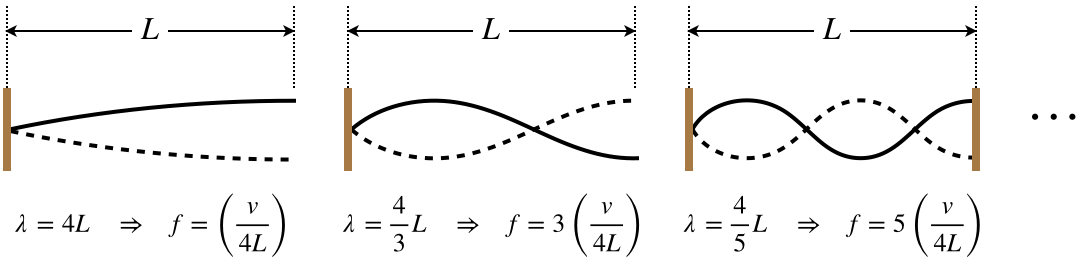
Notice that in this case each time a half-wavelength is added, the frequency jumps an amount equal to two fundamental harmonics. So for the case of one end fixed and the other end free, the allowed standing waves include no even-numbered harmonics. Mathematically:
\lambda_n = \dfrac{4L}{n}\;\;\;\Rightarrow\;\;\; f_n=n\left(\dfrac{v}{4L}\right)\;,\;\;\;\;\;n=1,\;3,\;5,\;\dots
Example \PageIndex{1}
Two boards with nails separated by different distances are combined with uniform strings that have different lengths and masses, to form one-string guitars.
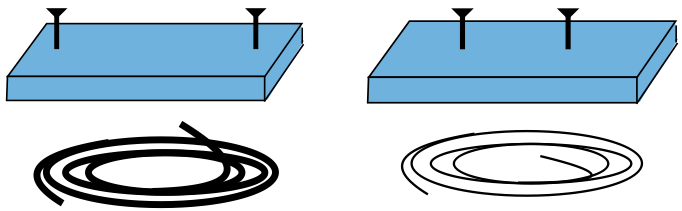
Show that these guitars make tones of the same pitch (as determined by their fundamental harmonics) when the following quantity \alpha is the same for both:
\alpha = \dfrac{FL}{md^2}\;,\nonumber
where F is the tension in the string, L is the length of the string, m is the mass of the string, and d is the distance separating the nails.
- Solution
-
The frequencies of the fundamental harmonics must be equal, which means:
f_A=f_B\;\;\;\Rightarrow\;\;\;\dfrac{v_A}{\lambda_A}=\dfrac{v_B}{\lambda_B} \nonumber
With both strings exhibiting their fundamental harmonics, they both have the same relationship between their wavelengths at the nail separations – in both cases the nail separation is half a wavelength:
\lambda_A=2d_A\;,\;\;\;\lambda_B=2d_B \;\;\;\Rightarrow\;\;\; \dfrac{v_A}{d_A}=\dfrac{v_B}{d_B}\nonumber
The speed of the traveling waves that create the standing wave is determined by the tension and the string density. The string is uniform, so its density is the ratio of the string's mass and its length. Therefore:
\mu = \dfrac{m}{L} \;\;\;\Rightarrow\;\;\; v=\sqrt{\dfrac{F}{\mu}} = \sqrt{\dfrac{FL}{m}}\nonumber
Plugging this in above gives:
\dfrac{1}{d_A}\sqrt{\dfrac{F_AL_A}{m_A}}=\dfrac{1}{d_B}\sqrt{\dfrac{F_BL_B}{m_B}} \;\;\;\Rightarrow\;\;\; \dfrac{F_AL_A}{m_Ad_A^2} = \dfrac{F_BL_B}{m_Bd_B^2} = \alpha \nonumber
Example \PageIndex{2}
Since the time of ancient Rome, commanders of armies have known that it is prudent to have the troops break stride in their march when crossing a wooden bridge. This is because if the troops march in a synchronized cadence, they produce a periodic coordinated jolt to the bridge, which could excite one of its natural harmonic frequencies, causing a standing wave to develop in the bridge.
- If a marching army does create a standing wave in the bridge, what aspect of this standing wave (A, f, T, λ) would be directly responsible for causing the bridge to break apart? Explain.
- Suppose a platoon comes upon a wood & rope bridge that is supported only at its two ends. The commander stops the company short of the bridge and shakes the nearest end of the bridge, testing to see if it seems strong enough to hold the troops. The bridge ripples all the way down its length, with the pulse reflecting off the other side and returning, for a round-trip time of about 2.5s. Find the frequency of the fundamental harmonic standing wave for this bridge.
- The commander decides the bridge is sturdy, and makes the tragic decision to order the company to march on. Their marching pace and spacing is such that a standing wave forms in the bridge, and the ropes break when the center of the bridge dips well below its usual point as two outer parts of the bridge surge upward. Find the marching pace of the company in steps per second.
- Solution
-
a. The bridge breaks apart when various components are stretched and separated so far that they can no longer hold together. This deformation of the bridge is a direct result of the amplitude of the standing wave. Put another way, the violence with which the bridge shakes is a measure of the energy put into it, and the energy in the standing wave is a function of its amplitude.
b. Call the length of the bridge L and the speed of the wave v. The time it takes the wave to travel two lengths of the bridge is given as 2.5s, and in terms of the distance traveled and speed of the wave, we have:
2.5s = t = \dfrac{2L}{v} \nonumber
For the fundamental harmonic, the length of the bridge (which is fixed at both ends) is one-half wavelength, so plugging in a half wavelength for L gives:
2.5s = \dfrac{2\left(0.5\lambda\right)}{v} = \dfrac{\lambda}{v} = \dfrac{1}{f} \;\;\;\Rightarrow\;\;\; f=0.40Hz\nonumber
c. The description of the standing wave makes it clear that it has three antinodes, which means it is the 3rd harmonic. The two ends of the wave are fixed, so the third harmonic occurs at three times the fundamental frequency, or 1.2Hz. For the footfalls to excite this harmonic, they need to match this frequency, so the marching pace is 1.2 steps per second.
Alert
If you are a musician, you likely have heard of overtones. At the simplest level (like one-dimensional standing waves with both ends fixed or free), these are synonymous with harmonics. But in the one-dimensional case when one end is free, or in the case of two-dimensional standing waves (like those produced by a membrane on a drum), these definitions diverge. We will not go into the details of these divergences, and the rare times we refer to the "first overtone," we will mean simply the next highest allowable harmonic.
Energy In Standing Waves
Let’s consider the case of a second harmonic standing wave on a string between two fixed ends. We know the following things to be true:
- Between the endpoints, there is exactly one full wave moving right and an identical full wave moving left at all times.
- Each of these waves contains an amount of energy that is proportional to the square of its amplitude.
- The standing wave has an amplitude twice as great as the amplitude of each individual traveling wave.
So the question is, doesn’t doubling the amplitude mean the standing wave has four times the energy of an individual traveling wave? If it does mean this, where does this extra energy come from, if there are only two such waves providing energy?
This apparent paradox stems from something we discussed earlier – it is dangerous to think of a standing wave in the same context as a traveling wave! This is especially true in the context of energy distribution. Let's consider the energy of a single particle in a medium as a harmonic wave passes through. Such a particle is following harmonic motion, so if it happens to be at the crest or the trough of the wave, then its kinetic energy is zero, while its potential energy is a maximum. Conversely, if it is at the middle, then it has its maximum kinetic energy and no potential energy. But no matter where it is in the phase of the wave, its energy is the same.
Now compare that with a particle in the medium of a standing wave. If the particle is at a node, then it never moves, and is never displaced from equilibrium, so its energy is zero. A particle at an antinode, on the other hand, has lots of energy. The amplitude of its harmonic motion is twice the amplitude that a particle on one of the two traveling waves would have, if the second wave wasn't there.
The bottom line is that the standing wave, when viewed as an interference pattern, clearly just redistributes the energy of the two traveling waves (which themselves distribute the energy uniformly), taking energy away from some regions of the medium and giving it to others. With some clever calculus, we can show that this works out exactly.
If the string has a linear density of \mu, then an infinitesimal segment of the string of length dx has a tiny mass of dm=\mu dx. A traveling wave has every such infinitesimal segment oscillating with the same amplitude, so every particle on the string contributes the same infinitesimal energy, and adding these contributions for a full wavelength gives:
E_{traveling\;wave}=\int\limits_0^\lambda \frac{1}{2}dm\;\omega^2A^2 = \int\limits_0^\lambda \frac{1}{2}\mu dx\;\omega^2A^2
The density of the string, the frequency of oscillation, and the amplitude of oscillation are the same for every particle in the string, so they do not vary with x, which makes the integral simple to perform:
E_{traveling\;wave}=\frac{1}{2}\mu\lambda\omega^2A^2
The segments of the string for a standing wave behave differently. They all vibrate harmonically (with the nodes exhibiting zero vibration), but they reach different maximum displacements. Put another way, a standing wave is a collection of an infinite number of harmonic oscillators, all with different amplitudes. So we need to write down the energy for each particle, and add them all up. The waveform of the standing wave gives us the amplitude (which we will call a\left(x\right)) of particle oscillation as a function of position x, so from Equation 1.5.7, we have:
Amplitude\;of\;medium\;at\;x = a\left(x\right) = 2A\sin \left(\dfrac{2\pi x}{\lambda}\right)
Recall that A is the amplitude of the two traveling waves that are interfering. The energy of this tiny piece of the string is:
dE = \frac{1}{2}dm\;\omega^2\big[a\left(x\right)\big]^2
Putting in dm=\mu dx and a\left(x\right) and integrating over the full wavelength of the wave, we get:
E_{standing\;wave}=\int\limits_0^\lambda \frac{1}{2}\mu dx\;\omega^2\left[2A\sin \left(\dfrac{2\pi x}{\lambda}\right)\right]^2
Making the substitution u\equiv\frac{2\pi x}{\lambda} leaves an integral that is easy to look up, and gives the following answer:
E_{standing\;wave}=\dfrac{\mu\lambda\omega^2A^2}{\pi}\int\limits_0^{2\pi}\sin^2u\;du = \mu\lambda\omega^2A^2
Comparing this with the answer for the traveling wave, we see that it is twice as much – the energy content of the standing wave equals the sum of the energies of the two traveling waves that interfere to create it. If we want to write the energy contained in a single wavelength of a standing wave in terms of the standing wave's "amplitude" (the amplitude of the harmonic motion located at an antinode), we have:
\mathcal A = 2A \;\;\;\rightarrow\;\;\; E_{standing\;wave}=\frac{1}{4}\mu\lambda\omega^2\mathcal A^2


