5.1: Background Material

Last updated
Save as PDF

Page ID: 28053

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Text References

Non-Ideal Springs

We found the potential energy function for a spring by computing the work done by that spring. This assumes that the spring is "ideal," which means that it perfectly obeys Hooke's law. It turns out that many real springs don't closely approximate this behavior. The springs used in this lab are no exception.

The spring used in this lab pulls its coils tightly together. That is, the pull of the spring is not zero when the spring is at its minimum length – the pull is balanced by the repulsive normal force between the coils that are in contact. If we hang a small weight from these springs, the coils don't separate. With no change in coil separation, the spring force doesn't change – the contact forces between them just get a bit smaller. Eventually, when we add sufficient weight, the coils do separate, causing the spring force to increase (and of course the contact force between coils vanishes, as they are no longer in contact). But the force exerted on the spring does not exhibit Hooke's law, which means that the potential energy stored in the spring can not be computed in the usual way.

Figure 5.1.1 Coil Behavior for Our Non-Ideal Spring

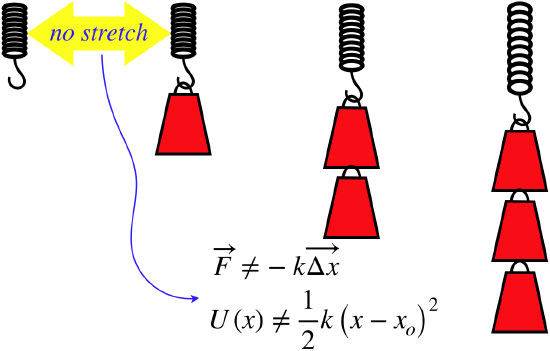
This doesn't mean we can't do anything with these springs, because we can still measure the displacement for various forces, which means that we can still compute the work done on the spring by stretching it. Of course, we need to know how the force changes as a function of the displacement to do the work integral – we can't simply multiply the force by the displacement.

Figure 5.1.2 Graph of Applied Force vs. Spring Stretch

The graph above shows how the spring behaves when certain forces are applied to it (in our experiment, we will do this by hanging weights). Imagine applying force \(F_A\) first, and noting the amount that the spring stretches \(x_A\). When we reduce the force to \(F_B\), naturally the spring stretch decreases (to \(x_B\)). As long as the coils don't touch each other, this follows a linear relationship, as we would expect for any spring. But when we reduce the force to the point where the coils are in contact (\(F_C\)), then every applied force from there down to zero produces the same stretch – zero.

When we store potential energy in a spring, we do this by doing work on the spring, and for a perfect spring, this work happened to equal the potential energy function \(\frac{1}{2}kx^2\) that we are so familiar with. But this is not such a spring, so to determine the potential energy stored in the spring, we must do a new calculation of the work done on it, using the function \(F(x)\) that we will determine experimentally.

Gravitational Potential Energy of Extended Objects

When an object changes heights, its gravitational potential energy changes, which is proportional to its change in height. When the object is not a point mass (i.e. it has extension in space), different parts of the object can be at different heights. How do we measure the change in potential energy, when there are so many points to choose from? What happens if the object rotates as it rises? The answer (which we will proved later in the course) is that this potential energy is computed using the change in height of the object's center of mass. Keeping this in mind for the spring, which actually changes length during its journey will be useful.