2.2: Effects of Force
- Page ID
- 18388
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Newton's Second Law
We have built some tools for analyzing situations where forces act on objects (force phrase, FBDs), and we know that there can only be accelerations when forces are present (first law). But we still are not yet able to describe the motion of an object under the influence of one or more forces. That’s because the first law only tells us qualitatively what is happening. In physics we seek to develop quantitative models, and that’s where the second law comes in. It is really just a more detailed description of the first law, or alternatively, the first law is just a special case of the second law.
We know that force is related not to velocity (because the first law says that constant velocity exists in the absence of force), but rather the change of velocity. More specifically, the rate of change of the velocity – the acceleration. Newton defined force in the simplest possible fashion in terms of acceleration – with a linear relationship. He knew that pushing equal amounts on two objects of different masses resulted in different changes of motion, so he stated that the relationship between force and acceleration as a simple proportionality:
\[ \text{acceleration of object} = \dfrac{\text{force acting on object}}{\text{mass of object}} \]
The idea is that for a given force, the reaction of the object (in the form of an acceleration) is inversely-proportional to the amount of mass the object possesses. Let’s take a moment to mention units:
\( \left[ F \right] = \dfrac{kg \cdot m}{s^2} = \; \text{"Newtons"} \; \left( N \right) \)
There is much more detail lurking in here. First of all, acceleration and force are both vectors, while mass is a scalar, so the second law is actually a vector equation:
\[ \overrightarrow a = \frac{\overrightarrow F}{m} \]
This means that the acceleration experienced by an object is just a scaled vector of the force exerted on the object. That is, the acceleration and the force always point in the same direction (mass is never negative). Of course, the scaling also changes the units.
ALERT
Most people first encounter Newton's second law expressed as \( \overrightarrow F = m \overrightarrow a\). While this is mathematically equivalent to what is above, it is very dangerous to write this way, as it encourages a very common misconception. We write it as we do above to emphasize the interpretation: "the effect on the motion (the acceleration) results from the cause (the force), moderated by a property of the object experiencing the effect (the mass)." The danger of using the other expression is that it reads like, "the force of the object equals the mass of the object multiplied by the acceleration of the object." This turns the quantities of force and acceleration into properties of the object, rather than cause and effect, and this leads to subtle but important misconceptions.
We aren’t done modifying the second law to its proper form yet! We know from our discussion of force diagrams that a large number of forces can be on an object at the same time. Which force is the one that causes the acceleration? All of them. Do we figure out the accelerations of each force and then add them up? That makes no sense physically – objects do not experience lots of accelerations at once. Instead, we take all of the forces together and add them as vectors to create a single composite force we call the net force, and that is what goes into the equation:
\[ \overrightarrow a = \dfrac{\overrightarrow F_{net}}{m} \]
Still not done! Suppose only a single force is acting on a specific point of an extended object? Remarkably, it doesn’t matter where the force acts on an object, if you measure the motion of the center of mass of the object (a quantity we will examine in more detail later on), it is the acceleration of that point that is determined by the force and mass.
Figure 2.2.1 – What Part of an Extended Object Accelerates According to the Second Law?
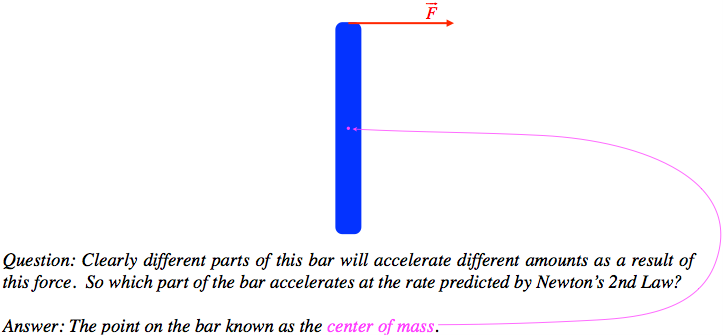
So finally we have arrived at the full-blown version of Newton's second law of motion:
\[ \overrightarrow a_{cm} = \dfrac{\overrightarrow F_{net}}{m} \]
Now perhaps the main point of the free-body diagram is clear: The diagram facilitates our ability to add force vectors (all of which are on the object, not by it), giving us the net force acting on it. We use the usual tools for vector addition to obtain this net force, perhaps expressing it in terms of its components in some coordinate system. Then we divide this vector by the mass of the object, and we have the acceleration of its center of mass, which could also be expressed in terms of its components. Then the acceleration is used to describe the object's motion as we have used it in kinematics.
Example \(\PageIndex{1}\)
A driver steps on the brake pedal of her car, slowing the car down, and her body experiences an acceleration as a result. Which of the following forces does Newton’s 2nd Law include when determining her acceleration?
- normal force by driver’s foot on the brake pedal
- friction force by the car tires on the road
- friction force by the road on the car tires
- all of these
- none of these
- Solution
-
(e) One must be very precise when it comes to identifying forces, as ultimately they must be plugged into a mathematical formula. It is not enough that a force sets off a chain of events that leads to an acceleration, it must be the direct effect of that acceleration in order to be the force that is featured in the second law. In addition to being a direct force, it isn't even sufficient to isolate the correct interaction – the specific "twin" from the third law force pair must be identified. That is, the force must be on the object in order to accelerate it. The problem asks what force slows down her body. The normal force on the brake pedal affects the motion of the brake pedal. The friction force on the road affects the motion of the road. The friction force on the tires (which are part of the car's system) affects the motion of the car system. While parts of the car system (namely tension by the seatbelt, friction by the car seat, and normal force by the steering wheel do slow her down, and the friction force on the tires slows down the car, this chain of events does not mean that the friction force slows her down. If you plug the friction force on the tires and her body's mass into the second law, the acceleration you calculate for her will not be correct.
Example \(\PageIndex{2}\)
A boy throws a ball straight up, and catches it when it returns. Which pair of diagrams best represents the directions of the net forces experienced by the ball when it hits the peak of its flight (i.e. when it isn’t moving), and while the boy is catching it (i.e. not after he has caught it)?
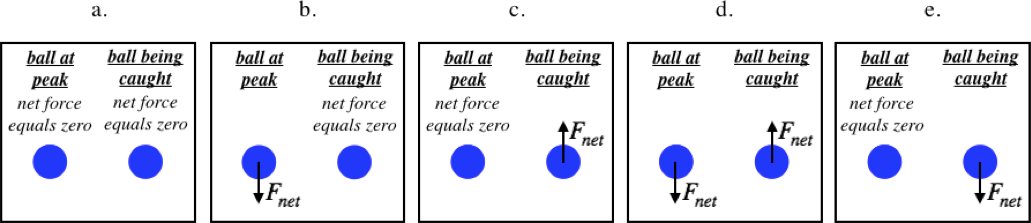
- Solution
-
(d) Gravity is always acting on the ball, no matter where it is. When it reaches its peak, there are no other forces on it (the boy’s hand is no longer in contact with it), so the gravity force is the net force, and it points down. When the ball is in the process of being caught, there is a force up on it by the boy’s hand, and since the ball is moving downward and is slowing, it is accelerating upward, which means the force from the boy's hand exceeds the force of gravity and the net force is upward.
Combining Newton's Second and Third Laws
We already saw in the case of the tug-o-war how the second and third laws work together: Each participant exerts an equal tension force on the other. These forces don't cancel because according to the second law, it is only the forces on the system that cause it to accelerate, and these two forces act on different systems. One individual feels this tension force on them, and if it is the only force, it will accelerate them forward (i.e. they will lose). To counter this, this person pushes the ground forward with their feet. But this is a force on the ground, which can only affect the acceleration of the ground, not the person, according to the second law. But now the third law comes to the rescue – when the person pushes on the ground, the ground pushes back equally, and this force is on the person. This opposes the pull of the rope, and if it is stronger than the rope's pull, the net force on the person is backward, and that person wins.
Another question that can be very confusing at first about the third law is this:
Another Puzzling Question: If the gravity force on a rock by the earth is equal and opposite to the gravity force on the earth by the rock, then why doesn't the earth accelerate upward when a rock is dropped to the ground?
As you might have guessed from the title of this section, it is the second law that comes to the rescue here. The answer is that the earth does accelerate up toward the rock! It feels the same net force that the rock feels, thanks to the third law. But when it comes to the acceleration, we need to divide this net force by the mass of the accelerated object, and since the mass of the earth is so much greater than that of the rock, it experiences a much, much smaller acceleration – so much smaller that it is imperceptible.
Finally, for a complete combination of all three of Newton's laws of motion, consider this: You are floating by yourself, untethered and weightless in outer space, mere feet from the hatch to the space station. To get there, you think of the idea of grabbing your own space suit and pulling yourself toward the hatch, and naturally it doesn't work (how you made the space program with such nutty ideas is a mystery). Why doesn't this work? Clearly you can exert a force on your space suit, which should result in an acceleration of that object, right? Well, in this case the relevant "system" is your entire body (you can remove your space suit and accelerate it to the hatch if you like, but that is not advisable). The system of your entire body includes your hand, which is doing the pulling, and experiences the third-law-pair force of the space suit pulling on it. If you draw the free-body diagram of your body and include the force on your suit as well as the force on your hand (both are acting on the system), then they clearly cancel. This had better be the case, because if it wasn't, it would mean that objects can just accelerate themselves, which violates Newton's first law of motion!
A Summary of Concepts Related to Newton's Laws
Much of what we have discussed in this section and the one before it will be repeated below, but putting all of these idea in one place may help the reader consolidate the ideas into a cogent "big picture."
- Force is not a quantity contained within an object.
- Forces are push or pull interactions between two objects. If one looks at the two individual forces that make up the interaction, then those two forces are always equal in magnitude and opposite in direction (Newton’s 3rd Law).
- To avoid confusion, we learned the all-important “force phrase,” which reminds us that the individual forces that make up the interaction force pairs always act on one object and by another.
- Forces are the cause of accelerations. It is impossible to have one of these without the other. This means that forces (if the vectors don't all cancel each other out) speed up, slow down, or change the direction of an object’s motion. And conversely, if an object’s motion slows down, speeds up, or changes direction, then it must be experiencing a (net) force. (Newton’s 1st Law)
- Forces are vectors, which is to say that they have magnitude and direction.
- The force vector that causes an object to accelerate is the net force on that object, that is, the vector sum of all of the individual forces exerted on the object. A net force is a combination of one or more real forces, but is not itself a type of force.
- Only the forces on an object can contribute to its acceleration (i.e. added together to give the net force), never the forces by it. Forces by an object only affect the motions of the other objects that they act on.
- The amount of net force on an object is proportional to the amount of acceleration it experiences, and the constant of proportionality is the mass, a measure of how much stuff is present in the object. (Newton’s 2nd Law)
- The fact that net force and acceleration are proportional means that as vectors, they must point in the same direction, since mass is never negative.
- Mass is sometimes called “inertia,” which can be loosely thought of as resistance to acceleration. But this must not be confused with resistance to motion – the smallest net force will cause an acceleration of the largest mass. If a mass at rest doesn’t start to move when a small individual force acts on it, it is because there is another force balancing it out, causing zero net force, not because the inertia of the object cannot be overcome.
- The part of the object that experiences the acceleration described in Newton’s 2nd Law is the center of mass of the object, not the point on the object where the force is acting.
- A useful tool for analyzing forces is the force diagram, which consists of isolating an object (which is why it is called a “free body diagram”), followed by drawing in all the force vectors acting on it. Careful use of the force phrase helps us avoid putting incorrect forces on this diagram.


