2.3: Types of Forces
( \newcommand{\kernel}{\mathrm{null}\,}\)
Gravity
We already know something about gravity from our study of free-fall and projectile motion. We know that the acceleration is the same for objects of different masses. While we have used this as a model, it is a big step to claim that gravity fundamentally follows this rule. We know that a feather will experience the same acceleration due to gravity as a stone, if air resistance is removed. Now how do we put air resistance back into our model so that the reduced acceleration of the feather makes sense?
The effect of reduced acceleration is easy to show with a FBD of two objects that are identical except for mass and are falling through the air at the same speed. For these two objects the air resistance forces are equal, and the gravity force is greater on the heavier object. The net forces on the two objects are therefore different, giving the following accelerations:
a(heavy)=Fgravity(heavy)−Fairm(heavy)a(light)=Fgravity(light)−Fairm(light)g=Fgravitym}⇒a(heavy)=g−Fairm(heavy)a(light)=g−Fairm(light)
So the reason the heavier mass accelerates more is simply that the effect that the air resistance force has on it is smaller. Care must be taken not to draw quick conclusions, because it is possible to draw an incorrect conclusion about a single force by not paying attention to a second force that is present. One simple result comes out of the free-fall case without air resistance:
Fgravity=ma, a=g ⇒Fgravity=mg
Alert
It is important to understand that here g has a different meaning than it had when we were discussing motion involving gravity-caused acceleration. Here the g is a physical constant, which we use to determine the gravity force on an object with mass m. It does not mean that the object is accelerating at 9.8ms2! When an object experiences no other force than gravity, the object's acceleration just happens to equal this constant, but the constant is present regardless of the state of acceleration of the object.
Tension
When we model problems that involve tension forces exerted by strings or ropes, we usually assume that the string or rope has no mass. Not to do so brings in some challenging (but interesting!) complications that are generally not the focus of that problem. For example, imagine two people having a tug-o-war, where one person is winning, and is therefore accelerating the other. A FBD of just the rope shows two forces on it (if we ignore gravity), one in each direction. With one of the people winning, not only do both people accelerate, the rope does as well. This means that there is a net force on the rope, and therefore one person is pulling on the rope harder than the other person.
By assuming that the rope is massless, the mass-times-acceleration for the rope is just zero, which means there is no net force on it, despite the fact that it is accelerating. With no net force on it, the two combatants are pulling on it with equal force, which means that essentially the force one person exerts on it is transmitted through the rope to act on the other person. That is, the rope becomes no different than a case of the two people clasping hands and pulling on each other. This allows us to use ropes as an idealized means of allowing the “by” object to exert a force “on” another object from a distance. Without this device, we would either have to devise examples in an awkward manner, or overly-complicate problems by including accelerating massive ropes.
Alert
Occasionally ropes will be used as a conduit for expressing third-law pairs (“tension force on A by B,” where neither A nor B is the rope), but this is dangerous, because ropes can also transmit the force around a pulley, in which case the Newton's third law pair of forces are clearly not in opposite directions.
Pulleys are another aspect of tension we should say a word about. If a pulley experiences friction as it rotates, or has some mass (so that its rotation requires the acceleration of some mass), then the tension force is not transmitted around it unaffected. We will actually look at the case of pulleys with mass later in the course, but for now we idealize them as we do ropes – no friction and no mass.
Normal (Contact) Force
What makes the contact force different from some others is that it is nothing more than a “balancer.” This means that its magnitude is determined not by independent criteria but rather by the details of the contact. For example, if a block rests on a level tabletop, then the zero acceleration of the block means that the net force on the block is zero. The Earth exerts a gravity force downward on the block, so there must be a balancing force upward to result in zero net force. The only other force available here is the contact force, so its magnitude adjusts to equal the force of gravity on the block. If we now tie a string to the block and pull up on it with a force less than the weight of the block, it maintains contact with the tabletop, and still remains stationary. This time for the forces to balance, the amount of contact force necessary to create balance is reduced by the amount of tension force the string provides.
The primary place where this feature of contact force comes up in problems is when a scale (like one you stand on in your bathroom) is involved. We are used to thinking of a scale as something that measures weight, but this is not the case – it measures contact force! For proof, just imagine pushing a scale against a vertical wall, rather than standing on it.
Kinetic Friction
Probably the most complicated and difficult to understand of the forces we have mentioned so far is friction. The microscopic mechanism is not even that well understood, partly because it has two different modes. This first of these modes comes from the fact that the two surfaces can be highly irregular. The second mode involves adhesive bonds that are formed between the surface molecules for each of the objects involved. Note that the fundamental force involved in both cases is electrical in nature, but it is repulsive in the first case and attractive in the second.
Both of these modes lead to two different forms of friction. The first we will discuss involves two surfaces rubbing across each other. This is called kinetic friction. One might imagine a number of contributing factors that affect the amount of rubbing friction force that might exist between two objects, but for our macroscopic model we boil those factors down to just two. The first is another force – the normal force between the surfaces. The harder the surfaces are pushing against each other, the deeper the surface irregularities mesh, and the more molecules are brought together to bond. Experimentally, we find that the friction force grows roughly linearly with this normal force. All the remaining factors we lump into a single unitless constant that multiplies the magnitude of the normal force, known as the coefficient of kinetic friction:
fk=μkN
It is important to note that having the two objects moving while in contact does not ensure that kinetic friction is occurring – the surfaces need to be sliding across each other. For example, a ball rolling across a floor that is not slipping in any way is not experiencing kinetic friction.
Static Friction
The second form of friction is a little harder to grasp, though we are all aware of it. Instead of being a force that exists while two surfaces are sliding across each other, this type of friction is a reaction force that attempts to prevent two surfaces from sliding across each other. This force, known as static friction, is responsible for the phenomenon we experience when we try to slide something and fail until we make enough effort to get it sliding – with any smaller force the object stays put.
Static friction is very similar to contact force, inasmuch as it is merely a balancer. If you push on something hard enough that it begins to slide, then static friction no longer applies, but if it doesn’t start sliding, then it is because the static friction force balances that push, resulting in a zero acceleration. Unlike contact force, however, static friction has a maximum – if other forces are sufficiently great, the sliding will begin, and the friction force shifts from static to kinetic. This maximum is also lumped into a constant, but the relation between the friction force and the contact force is now an inequality:
fs≤μsN
The most common place that we encounter friction (kinetic or static) is for an object on a horizontal plane, such as a table on a floor or a plate on a table. When the surface is horizontal, the zero vertical acceleration means that the contact force equals the weight, which means that the friction force is directly proportional to the weight. Put another way, “Heavy things are hard to slide across the floor.” But this jump is not a good one to make, since not all surfaces are horizontal (and acceleration is not always zero, e.g. in an elevator). The magnitude (or maximum magnitude) of the friction force is determined by the contact force – not by the gravitational force, and certainly not by the mass of the object.
A phenomenon we are all familiar with is that for the same two surfaces in contact, the coefficient of static friction is greater than the coefficient of kinetic friction. That is, it is more difficult to get an object sliding across a surface than it is to keep it sliding across it. This can be understood conceptually by thinking about the two microscopic modes we discussed earlier. When the surfaces are sliding across each other, the irregularities don’t have time to settle into each other, and the molecular bonds are being broken and re-formed, and in the period before re-forming there is no force.
This phenomenon is the main culprit behind what many people mistakenly refer to as "inertia." The physical concepts involved are insidiously subtle: Someone pushes an object across a floor, accelerating it from rest, and notices that it is harder to get it going than to keep it going. Then they try to push a bigger object and finds it even more difficult to get started. They draw the conclusion that the greater mass of the second object means it "has more inertia to be overcome" to get it going. Indeed, these people may have even heard of the "law of inertia," and know that mass is related to inertia.
We now have the tools to debunk this analysis. The "law of inertia" is Newton's first law. This law says that the object being pushed "wants" to remain stationary, but the law does not provide for a minimum force necessary to overcome the object's "desire" to stay in place. The effect of a push on the object is determined by Newton's second law, and no matter how large the mass is, or how small the net force is, a non-zero acceleration will result. The correct explanation for this apparent inertia phenomenon is this: For an object on a horizontal surface, the normal force equals the gravity force. The gravity force is proportional to the mass of the object (it equals mg), so the normal force is proportional to the mass. The maximum static friction force is proportional to the normal force, so it too is proportional to mass. Therefore the amount of force required to get something sliding on a horizontal surface happens to be proportional to the object's mass. But this is not an intrinsic property of mass - there are many important steps between the amount of mass and this thing people call "inertia." It is dangerous to jump to quick conclusions without a careful analysis.
Application: Anti-Lock Brakes
The fact that the coefficient of kinetic friction is greater than the coefficient of static friction for the same surfaces has its greatest application in an invention called “anti-lock brakes.” When a tire is rolling perfectly over the road surface, the surface of the tire is not sliding across the surface of the road, which means that if any friction is involved, it is static friction. If you apply the brakes, the tires’ rotation will slow down until the static friction maximum is exceeded, at which point the tires will stop turning and the tires will slide across the road surface. The friction force on the tires goes down when this occurs, because the kinetic friction is smaller than the maximum static friction. So an ABS system automatically releases the breaks briefly so that the tires again turn, restoring perfect rolling and allowing the return of static friction. This would be like trying to push a heavy cardboard box across a floor in extremely short bursts – as soon as the box starts sliding (and gets easier to push), you stop and start over. Before the invention of ABS systems, drivers were told to "lightly pump their brakes" in slippery situations to create this same effect. ABS systems do the pumping for us, with a much greater frequency than we could manage, and to great effect.
Air Resistance (Drag)
Air resistance is sometimes referred to as “air friction,” but although it has dissipative qualities similar to those of friction (as we will see when we study energy), the mechanism by which it functions is quite different. Air resistance occurs because of countless collisions between the microscopic particles that comprise the atmosphere and a macroscopic object moving through it. There can be no collisions without motion, so unlike friction there is no “static air resistance.” In this class we really won’t deal with air resistance in a rigorous mathematical way, primarily because fluid dynamics is an especially complicated subject (this is why we simplify projectile problems by assuming no air resistance). But we can determine a few characteristics that make sense:
- cross-sectional area – Anyone who has ever put their hand out the window of a moving car knows that the air pushes it back with greater force when the palm faces forward than when it faces downward. The difference is the cross-sectional area, and that is important because the greater this value is, the more atmospheric particles per second can hit the hand. Obviously if the area is doubled, the number of particles hitting the object per second is doubled, so the drag force is directly proportional to the cross-sectional area.
Alert
"Cross-sectional area" is not the same as "surface area." The surface area of one's hand doesn't change when it is rotated from a palm-forward position to a palm-downward position when the hand is held out the window. What matters is the area perpendicular to the relative velocity of the incoming particles that comprise the air.
- speed – Returning to the common experience of holding a hand out of a moving car window, we know that the faster the car is going, the greater the force is on our hand. In this case the exact mathematical relationship is not as obvious as it was for cross-sectional area. In fact, it can depend upon the relative air speed differently for different air speeds (or more accurately, whether the air flow is orderly or turbulent).
- air density – Density is a measure of how many particles you find in a given small region of space. If the air is very dense, then there are more particles that can strike the cross-sectional area than if the air is less dense. So the drag force is directly proportional to the density of the air.
We will not write down or have use for a specific equation for air resistance, but we can use the facts above to draw some conclusions. Imagine you have just jumped out of a plane, and the Earth’s gravity begins accelerating you downward. This acceleration results in your speed getting greater and greater, and as it does, the air resistance force upward on your body also gets greater. Of course, your downward acceleration is determined not by gravity alone, but rather by the net force on your body, which is reduced as the air resistance (which opposes gravity) grows. Eventually you end up going fast enough that the air resistance force equals your weight, and you stop accelerating. The speed at which this happens is known as terminal velocity. Notice that when you pull your ripcord and your parachute deploys, you increase your effective cross-sectional area, and to achieve the same amount of drag force, not so much speed is required. This is good, because it allows you to hit the ground with a speed that is not … um… terminal.
Elastic (Spring) Force
To close out the section on details of forces, we'll look at one not yet mentioned. Actually, it can fall under the categories of both tension and contact force (and is therefore both attractive and repulsive), but it has the nice feature that we can deal with it a bit more precisely mathematically. It is called the elastic or spring force. The characteristic feature of this force is that it acts in a restoring fashion (and is therefore a type of restoring force), meaning that there exists an equilibrium status, and any deviation from this equilibrium leads to a force acting to return the object to the equilibrium state.
Figure 2.3.1 – Elastic Restoring Force
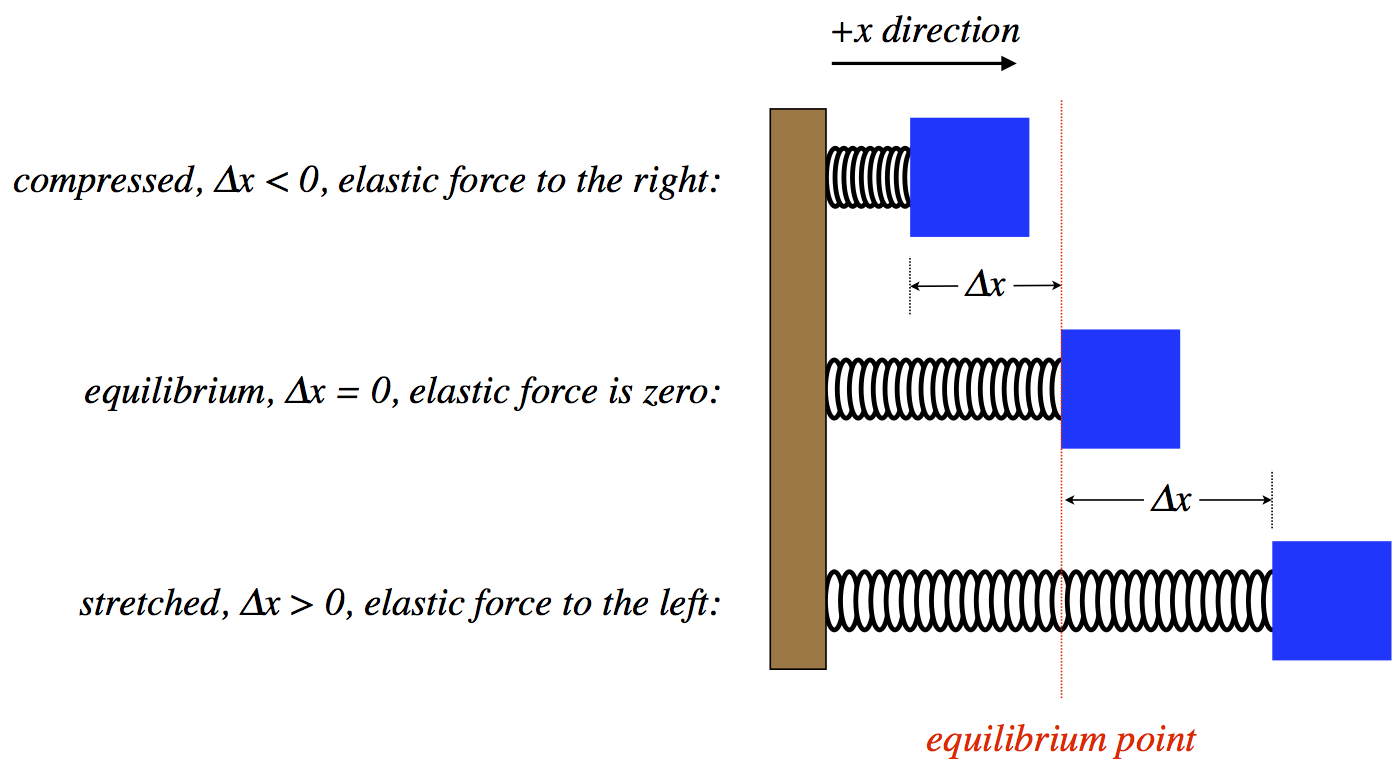
In particular, the elastic force is proportional to the separation of the object from its equilibrium position:
This force always points from the point to which the object is displaced back to the equilibrium point. The constant k is known as the spring constant, and has units of Newtons per meter. It is a measure of how “stiff” the spring is (i.e. how difficult it is to stretch or compress). As always, it is important to keep in mind that this is a model for the spring force. Actual springs typically deviate from this behavior, in some cases significantly. But the usefulness of this model in physics cannot be overstated. Indeed this model has found its way into literally every corner of physical theory.
While Equation 2.3.5 describes the elastic force well, there is actually a nice way to express it in a compact manner as a vector equation. Treating displacement from the equilibrium as a vector, we see that the direction of the force is in exactly the opposite direction, regardless of whether the spring is stretched or expanded. Accordingly, we can write:
→Felastic=−kΔ→x
This equation is commonly known as Hooke's law.
Alert
Note that the usage of the "Δ" in Hooke's law is different from how we have used it up to this point – here it refers to a difference in positions, rather than a difference of after and before.


