2.1: Properties of Force

Newton's First Law

We now understand how to handle motion in all its forms, but really we haven’t done much in the way of physics, because we haven’t explained what causes these different motions. In ancient times, Aristotle made the observation that eventually all things seem to come to rest, which led him to conclude that a stationary condition was “natural” for everything (well, everything on Earth – heavenly bodies never seemed to stop moving). He stated that keeping things moving requires constant pushing or pulling, or it would eventually settle into a state of rest.

This is a very intuitive way of describing the nature of things, and most people even today see the world this way. It wasn’t until nearly 2000 years after Aristotle that a genius born on Christmas day would overturn that long-held belief. His name was Isaac Newton, and he claimed that in fact nature behaved in precisely the opposite manner. Newton claimed that it was not natural for objects to be at rest unless they were already at rest. If they were already moving, then it was natural for them to continue moving. He claimed that it was the fact that objects on Earth could not escape pushes and pulls that accounted for them always coming to rest.

But Newton was more specific about this “natural state of motion.” He stated that the only type of motion that would continue indefinitely if undisturbed by pushes or pulls was constant velocity (speed and direction) motion. That is, any motion that involved changes of speed or direction requires a push or pull.

Newton's 1st Law of Motion

Objects at rest or in motion at a constant speed in a straight line will remain in that state unless acted upon by an external influence.

Definition of Force

What we have been calling “pushes and pulls” or “external influences” is called force in physics. Most people have an intuitive idea of what force is, and like so many other physics concepts, this intuition is likely wrong. We'll start by saying what force is not, then move on to its definition.

Alert

Force is not a quantity stored in, or possessed by, an object. Force cannot be transferred from one object to another, nor can one claim that one object “has” more force than another. This can be a hard notion to shake.

Definition: Force

Force is an interaction between two objects, which comes in the form of a push or a pull.

When this interaction occurs, each object is affected by the other, and there are always two objects involved. As you begin your exploration into the concepts related to forces, it is a good idea – at least for awhile – to adhere to a very strict structure of wording when describing a force. Doing so will help you avoid common pitfalls in understanding. After awhile it is okay to abbreviate the description some, but if confusion ever returns when talking about a force, returning to the phrasing should help:

The "Force Phrase"

"...\(\left<type\;of\;force\right>\) on \(\left<object\;experiencing\;force\right>\) by \(\left<object\;exerting\;force\right>\)..."

The only part we are not yet ready to fill in is the type of force. So let’s take a moment to catalog a few types of forces that we will be working with. We will add more as the quarter goes on, but we need something to get started with for the sake of discussion.

Types of Forces

According to Newton, forces are interactions that cause objects to vary from their natural state of motion, but we can best describe them as pushes or pulls. We have already talked about one way to get objects to speed up, slow down, and change direction, and that is gravity. Gravity is a type of force, but what is more, it is what is referred to as a fundamental force. Essentially a fundamental force is one that acts rather mysteriously at a distance. Other examples of fundamental forces you are familiar with from your experience are the forces due to magnetism and static electricity (there are also nuclear forces that are fundamental with which you do not have direct experience). Every other force we will discuss in this class requires some kind of contact between macroscopic objects. This goes back to our notion of physics being about constructing usable models. Ultimately every push or pull breaks down to one or more fundamental forces, but (other than gravity), these forces are between microscopic particles, and we want our model to give results in the macroscopic realm.

So let’s name some of the other (non-fundamental) forces we will be studying, so that we have some common language. We will not discuss details of the properties of these forces just yet – we are just establishing some language so that we can describe forces in physical situations.

• tension – a pulling (attractive) force transmitted via a rope or string
• contact or normal – a pushing (repulsive) force resulting from direct contact of two surfaces [“normal” means “perpendicular”, and is appropriate because this force always acts at right angles to the surfaces in contact]
• friction – a force that occurs due to rubbing or attempted rubbing of two surfaces, which opposes the relative motion or attempted relative motion
• air resistance or drag – a force similar to friction that comes about because the atmosphere impacts with and rubs across the surface of an object moving relative to it

There are one or two more modeled forces we can (and will) add, but these are sufficient for our purposed right now.

Newton's Third Law

As is implied by the name “first law,” Newton was not finished – he posited two other laws of motion as well. We’ll return to the second law shortly, but first we will discuss the third law. You have almost certainly heard it before:

Newton's Third Law

For every action there is an equal and opposite reaction.

This is an extremely unfortunate use of language, and this law has been misinterpreted for hundreds of years as a result. It is often heard quoted in movies to essentially express how natural it is to seek retribution. Something like, if someone hits you, you will hit them back afterward.

ALERT

The idea of a “reaction” as we understand it in common parlance is that it is a consequence of a previous action, but this is not the way that Newton means it.

Okay, then, so how does Newton mean it? Forces are interactions, and just as it is impossible for a single hand to clap, it is equally impossible for a single object to be the sole participant in a force interaction. So if one object experiences a force from another, there must be a reciprocal force also felt in the other direction at exactly the same moment, with precisely the same magnitude and in precisely the opposite direction (yes, of course forces are vectors). So for every force you can name, there exists an evil twin that acts in the opposite direction with equal magnitude. These "twins" are often called Newton’s third law force pairs. The easiest way to identify these pairs is to use the force phrase for one force and then reverse the "on" and "by" to describe its third law pair.

Example \(\PageIndex{1}\)

A block weighing 12lb travels in a circular path in a vertical plane. As the block does this, it slides along a frictionless circular track, and it is also attached to a string, the other end of which is attached to a fixed point at the center of the circle. When the block is at the bottom of its circular path, the contact force exerted on it by the track equals the tension force exerted on it by the string, and both are equal to 12lb. Which of the following forces is the Newton’s 3rd Law pair corresponding to the gravity force on the block?

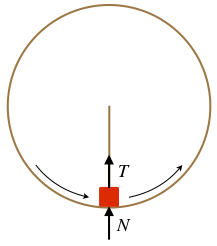
1. the normal force on the block
2. the tension force on the block
3. Either (a) or (b) can be considered a third law pair for the gravity force.
4. the sum of (a) and (b)
5. None of the above is a third law pair to the gravity force on the block.

Solution

(e) Don't let all the special information provided and coincidental numbers fool you! Just reverse the "on" and the "by" in the force phrase. The gravity force interaction is between the block and the earth, so the third law pair of the gravity force on the block by the earth is the gravity force on the earth by the block.

Now for a puzzler that gets to the heart of understanding the third law:

A Puzzling Question: When I push against the wall neither of us “wins” – I don't get the wall to move, and it doesn't get me to move. So it makes sense that the forces we exert on each other have to be equal-and-opposite. But if Newton’s Third Law applies to every interaction, how does anyone ever win, in say, a tug-o-war?

We’ll answer this question in a moment, but before we do, we'll need an extremely powerful tool for analyzing physical situations involving forces.

Free-Body Diagrams

Possibly our most powerful tool for analyzing forces and their effects on the motions of objects is the free-body diagram (or FBD for short). This is a diagram that consists of a single system (the "free-body," which can be a single object or a collection of objects with a collective fate), with arrows representing force vectors drawn on it. There are a few rules to drawing an accurate FBD:

• It must include only an isolated "system." This system can consist of one object or many, but the analysis that follows applies to the system as a whole, and nothing outside this system – whatever its role in the physics – is included in the diagram.
• The force vectors must be “real” forces. If you can’t name the force with one of the forces mentioned earlier, then you are probably trying to fix something that isn’t broken by inventing a force. Also, no forces calculated from aggregates of other forces should be included – just separate, physically-describable forces.
• Only forces on the system can be included – never forces by the system. If every vector is labeled using the force phrase, there is no way to go wrong here.
• For now, where the force vectors are located on the system is not important, so the entire system can be reduced to a single dot for simplicity. But later this quarter the location where the force acts will become important, so it might be a good idea to try to place the force vectors properly right away. Since the type of force and its basic nature are related to where it acts on an system, this will also help confirm that you are dealing with the right forces, and are not trying to invent a force that doesn't exist.

Okay, let’s return to the puzzling question... If two entities interact through (say) a tension force (this is fancy physics-speak for “two people have a tug-o-war with a rope”), and if they always experience the same force as the other person, how does one side ever “win?” Let’s draw a FBD to see if we can see why.

Figure 2.1.1 – Analyzing a Tug-o-War Using a FBD

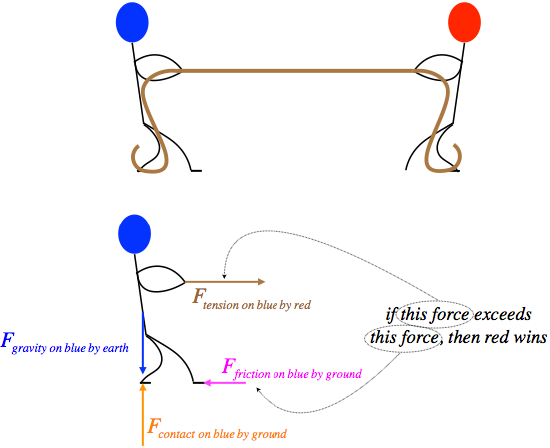
The reason the question is confusing is that we think that the two forces that are equal-and-opposite must always cancel out, but how exactly do forces “cancel?” They have to act on the same system. By drawing a careful force diagram in which we only include the forces on the system in question (in this case, the blue-headed stick figure), we see that in fact the force pairs that are equal and opposite are split ("tension on blue by red" is split from "tension on red by blue", and so on), and therefore cannot cancel each other. The real determining factor of whether an individual wins the tug-o-war is whether that individual receives a friction force from the ground that is greater than or less than the tension force, unbalancing the total horizontal force on them.

Does this mean the person is at the whim of the ground, that either decides to provide a big or small friction force? Of course not! The friction force on our feet by the ground is equal-and-opposite to the friction force our feet exert on the ground, and we do this by leaning back and sliding (or push our foot forward as if to slide it) across the ground. We can see that this is the case, because even the strongest human in the world cannot win a tug-o-war against a small child if the strong person is on ice or on some rolling device that doesn’t allow them to push horizontally (and thereby be pushed back the opposite way).