8.4: Coupled Oscillators and Normal Modes
( \newcommand{\kernel}{\mathrm{null}\,}\)
Multiple Springs
As the next step in our examination of small oscillation theory, we move from a single oscillator into combinations of oscillators. A very basic first step is to consider the effect of multiple springs on a single mass. We will keep the discussion basic by continuing to insist that the mass only moves in one dimension.
As a first case, consider the simple case of a mass attached to two different springs. We will call this case parallel springs, because each spring acts on its own on the mass without regard to the other spring.
Figure 8.4.1 – Two Springs in "Parallel"
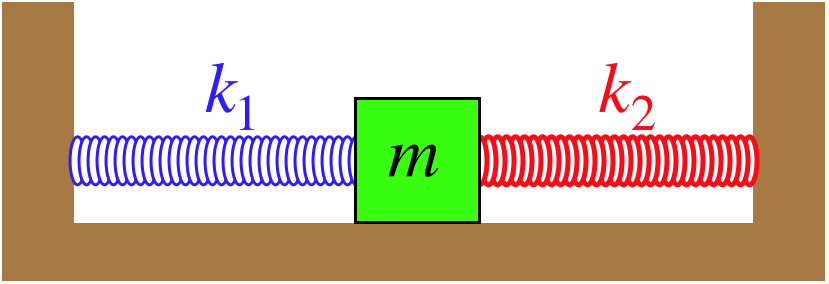
We will assume for simplicity that the mass is attached between the two springs when both are at equilibrium. This is not a necessary assumption, because if they are not at equilibrium, a new equilibrium point (where both springs are slightly stretched or slightly compressed) exists, not changing any of the analysis. Note that if we had placed both springs on the same side of the mass, then the physics would not be different from what we have here – instead of two forces in the same direction because one spring is compressed and the other expanded, the two forces would be in the same direction because both are stretched or expanded, and the magnitudes of the Hooke's law forces are the same in both directions.
This system behaves exactly like a single-spring harmonic oscillator, but with what frequency? To answer this, we basically need to find the single spring constant that is equivalent to these two springs. We can do this by displacing the mass a distance Δx and seeing what restoring force is the result for each case. As stated above, the forces by both springs are in the same direction, so:
two springs:|F|=k1Δx+k2Δxone "equivalent" spring:|F|=keqΔx
In order to be equivalent, these restoring forces must be equal, so we get a way of writing these two springs as a single equivalent spring:
keq=k1+k2
Simple enough, but now let's look at what happens if we connect the springs to each other. This configuration we call series, because the springs are in direct contact and therefore effect the mass by successive stretching. Note that in the parallel cases, the stretching was coincident rather than successive, and the resulting physical effect is different in the two cases.
Figure 8.4.2 – Two Springs in "Series"
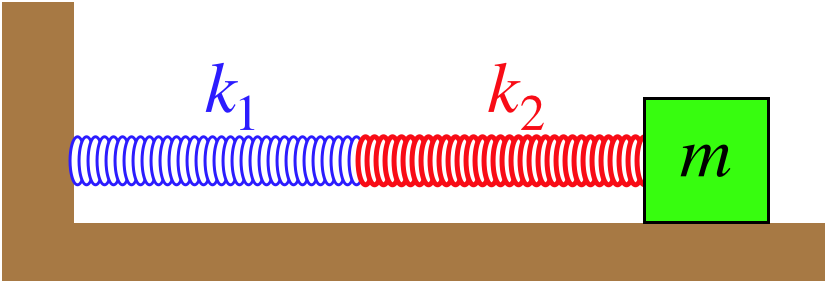
In this case, the springs are connected, which means that according to Newton's third law, whatever force is stretching or compressing one spring is also the force that is stretching or compressing the other, and this is also the force exerted on the mass. They have different spring constants, so the equal forces will stretch or compress them different amounts. If we are to combine them into a single equivalent spring, then the sum of the stretches or compressions will be the total displacement of the mass. We therefore have:
two springs:|F|=k1Δx1=k2Δx2one "equivalent" spring:|F|=keq(Δx1+Δx2)
Solving for Δx1 and Δx2 in terms of the force in the "two springs" equations and plugging them into the equivalent spring equation gives:
1keq=1k1+1k2
Coupled Oscillators
Our next step is to increase the number of masses. We already considered the case of two masses connected by a single spring in Section 8.2, but found that case to just be equivalent to one "reduced mass" on a single spring. Here we will introduce a second spring as well, which removes this simplification, and creates what is called coupled oscillators. Let's start with the simplest conceivable case – two identical masses connected with two identical springs to a single fixed point:
Figure 8.4.3 – Simple Coupled Oscillators
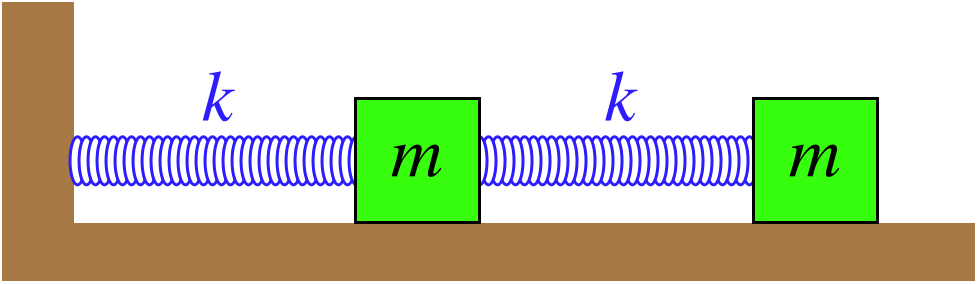
What makes this so much more complicated than the previous cases is that the "origin" for the second mass is moving, which complicates the measurement of the stretch or compression of the second spring. We begin by defining position variables for both blocks, and then use these variables to relate the forces on each. We actually have a great deal of freedom in defining how we measure the positions of the two blocks, and there is no reason to define a common origin for them, as long as we incorporate these variables into the dynamical equations correctly.
For this problem, we will define the origin of the left mass as its position when the left spring is at its equilibrium length, and the origin of the right mass as its position when both springs are at their equilibrium lengths. So if both blocks are at their origins, then there is no force on either block.
Figure 8.4.4 – Coordinates for Blocks

Now we need to make an accounting of the forces on each block according to the coordinates defined. The force on the right block is easy – it is determined only by the stretch or compression of the spring between the blocks. That stretch/compression is easily expressed in terms of the coordinates defined:
F2=−k(x2−x1)
Note that if both blocks move the same distance in the same direction from their origins, then x1=x2, and the force is zero because the spring between them isn't stretched. A bit of thought should also convince the reader that the sign on the force works out correctly for various positions for the blocks.
The force on the left block is only a little bit trickier, as there are two springs acting on it. The force on it by the spring between the blocks is the same as what we just found, but in the opposite direction, and the force on the left block by the left spring just follows the simple Hooke's law. The net result is therefore:
These two forces result in two differential equations when Newton's second law is applied in each case. Specifically, we have:
These coupled differential equations appear quite daunting to solve, but there is a trick for treating these systems, which we will examine next.
Changing Variables
It turns out that the system above for which we obtained coupled differential equations is a bit "ugly" inasmuch as the solution is not especially illuminating, so here we will examine a system with a bit more symmetry by adding another spring. To save space, we will include the two coordinate systems with the diagram.
Figure 8.4.5 – Coupled Oscillators With Three Springs
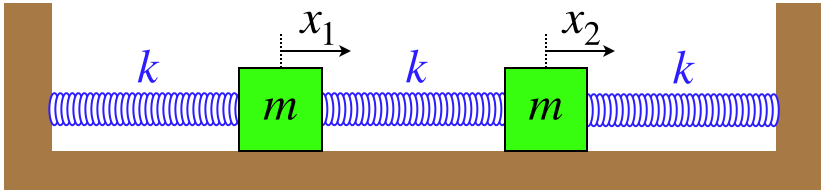
As before, we will define the origins of the two coordinate systems to be the equilibrium points, and as before, we need to express the net forces on each mass according to the positions. Clearly the equation for the force on the left mass is identical to the example above (Equation 8.4.6). We can work out the force for the second mass as we did before, but because of the symmetry of the situation, the equation for the net force on the right mass should look similar to that of the left mass:
left block:F1=−kx1+k(x2−x1)=−k(2x1−x2)⇒d2x1dt2+2kmx1−kmx2=0right block:F2=−kx2+k(x1−x2)=−k(2x2−x1)⇒d2x2dt2+2kmx2−kmx1=0
The symmetry in this physical system is reflected in these equations of motion, but we are no closer to a solution than before. Here is where our "trick" comes in. Add the two differential equations together to obtain a new equation:
d2x1dt2+d2x2dt2+2kmx1+2kmx2−kmx1−kmx2=0⇒d2(x1+x2)dt2+km(x1+x2)=0
If we define a new variable q1(t) (the reason for the subscript will soon become clear), a remarkable thing happens:
q1(t)≡x1(t)+x2(t)⇒d2q1dt2+kmq1=0
This new variable satisfies a differential equation that exactly describes harmonic motion with angular frequency equal to √km! It's not clear how to physically interpret this at the moment, so we will come back to it shortly, but at least we can write a solution for q1(t):
q1(t)=A1sin(ω1t+ϕ1),ω1=√km
This is not the only function we can find that has this property. Let's now subtract the two differential equations that we previously added:
d2x1dt2−d2x2dt2+2kmx1−2kmx2−kmx1+kmx2=0⇒d2(x1−x2)dt2+3km(x1−x2)=0
Again we define a new function q2(t) and get a result only slightly different from the previous one – the frequency of oscillation comes out to be greater by a factor of √3:
q2(t)≡x1(t)−x2(t)⇒d2q2dt2+3kmq2=0q2(t)=A2sin(ω2t+ϕ2),ω2=√3km
With these two solutions, we can now reconstruct the original functions, giving us the answer we were looking for:
x1(t)=12[q1(t)+q2(t)]x2(t)=12[q1(t)−q2(t)]
It should be noted here that the amplitudes of the two normal modes are free parameters, so the motions of the two blocks can essentially be any mix of the two q-function sinusoids. If one of the amplitudes is zero, then the blocks follow the simple harmonic motion of the remaining q-functions. While this looks like nothing more than a math trick that only works for a highly-symmetric problem, it actually displays a very fundamental principle used throughout physics.
Normal Modes
It turns out that the oscillatory motion described by the functions q1 and q2 can be observed in the physical system, given the proper circumstances. Suppose we displace both blocks in the same direction by the same amount, and release them from rest. In this configuration, the spring between them is neither stretched nor compressed, and the force each block feels will be caused only by the other spring attached to them. Since they have the same mass and were displaced equal amounts with identical springs, their motions will mirror each other, which means the center spring will never expand or compress. In this case, they will both oscillate like a single mass on a single spring – with a frequency equal to √km. This is exactly the frequency we found for q1. By displacing both blocks the same amount, we have set up the circumstances where the difference in their positions (measured by q2) never changes. By forcing q2 to remain constant, only the motion described by q1 is seen.
If we only want to witness the motion described by q2, we just need to set up an initial condition where the sum of the positions is unchanged. This corresponds to moving the blocks equal distances from their equilibrium points in opposite directions and releasing them from rest.
There are only two of these "special" modes of oscillation for this system, and these are called the system's normal modes. It turns out that these modes exist for every system, including those that are not symmetric (different masses, different spring constants, etc.). It also happens that there is a separate normal mode for every degree of freedom that the system possesses. By "degree of freedom" we mean essentially the number of variables we need to introduce in order to completely describe the evolution of the system. For example, if we added another block and another spring to the system above, then we would need another variable x3 to describe the motion of the third block, giving the system three degrees of freedom, and therefore three normal modes.
One useful way to think about normal modes is like unit vectors we use to describe the "vectors" that are the total motion of the system. Each mode is "orthogonal" to all the others, and when combined in proper proportions, they can build any of the complicated types of motion. Each mode has its own individual frequency (frequencies of different normal modes are sometimes equal to each other, typically due to a symmetry of the system).
Return to the "Simple" Coupled Oscillators
Armed with this idea of normal modes, let's take another shot at the system of coupled oscillators shown in Figure 8.4.3. We have our two differential equations that include x1 and x2 in Equation 8.4.7. Now we are looking for a pair of new coordinates, q1 and q2, that express the motions of the normal modes. In the highly-symmetric case that we just solved, we found that each of these normal mode functions was a simple combination of the individual object coordinates – q1 was the sum of x1 and x2, while (q_2\) was the difference. In this less-symmetric case, we need to assume that the combination is more complicated, so we'll write the following for a generic q (we'll see that the cases for the two separate modes come out automatically):
q(t)=α⋅x1(t)+β⋅x2(t),
where α and β are constants.
If we multiply the first differential equation in Equation 8.4.7 by α, the second by β, and add them together, we get:
d2dt2[αx1+βx2]+(2α−β)kmx1+(β−α)kmx2=0
The quantity in square brackets is just q. We are looking for a normal mode equation, so ultimately this needs to look like the equation for a simple harmonic oscillator with the angular frequency associated with this mode:
d2qdt2+ω2q=0
If we compare these last three equations, we see that the second derivative is already where we want it to be. To get the rest of the differential equation where it needs to be, we need:
(2α−β)kmx1+(β−α)kmx2=ω2q=ω2(αx1+βx2)
Collecting terms gives:
[(2α−β)km−ω2α]x1+[(β−α)km−ω2β]x2=0
The two masses do not have to always be at their origins at the same time, which means that the coefficients of x1 and x2 must each equal zero, giving:
(2α−β)km=ω2α⇒βα=2−mkω2(β−α)km=ω2β⇒αβ=1−mkω2
Now we can multiply these last two equations together to eliminate α and β, leaving us with a quadratic equation to solve for ω:
1=(2−mkω2)(1−mkω2)⇒ω=√3±√52√km≈1.62√kmor0.62√km
We see that the quadratic equation gives us two different possible frequencies – one for each normal mode. If we plug each of these frequency solutions back into Equation 8.4.20, we can determine the ratio of α and β for each normal mode, which gives us q1 and q2. [Note that we can never determine exact values for α and β – we can only find their ratios. For example, even in the symmetric case we could have chosen q1=0.3x1+0.3x2 and q2=0.3x1−0.3x2 and everything would have worked out the same.]
βα=2−3±√52=1∓√52≈−0.62or+1.62
If we just choose α equal to +1, then we can put this all together to summarize the two normal modes:
mode 1:q1=(+1)x1+(−0.62)x2ω1=1.62√kmmode 2:q2=(+1)x1+(+1.62)x2ω2=0.62√km
How do we interpret these modes physically? Mode 1 involves the two masses being displaced in opposite directions from their equilibrium positions at their turnaround points (i.e. they are always moving in opposite directions). Their maximum displacements are in the ratios given, so if the mass between the two springs is 1cm from its equilibrium when it stops, then the other mass is 0.62cm from its equilibrium (in the opposite direction) when it stops at the same moment. Mode 2 is interpreted similarly, except that the masses are always moving in the same direction, and a 1cm amplitude for the mass between the two springs results in a 1.62cm amplitude for the other mass. The system's frequency in mode 1 is greater than it is for mode 2, which makes sense if one visualizes the motions of the two modes – the first has the two masses going in opposite directions, not displacing that far, while the second mode has the whole system stretching far away from the wall, then compressing toward the wall.
There is an obvious symmetry between the two modes, where the ratios of the amplitudes of the masses match the ratios of the normal mode frequencies. This comes from the fact that the masses and spring constants are equal – the reader should not be fooled into thinking that this is a general feature of normal modes of coupled oscillators.
Finally, it needs to be emphasized again that these two modes are not the only ways that the system can evolve – they are just the only ways that the system will repeat itself periodically if the initial conditions are set up just right. If the masses are started in some non-normal mode condition (e.g. they are separated from their equilibrium points by amounts that do not satisfy either of the allowed proportions), then the motion will be a mix of the two modes, and will look very complicated, and will not repeat with the simplicity that the normal modes repeat.
Coming Attractions
When one obtains more mathematical tools (namely the matrix methods learned in linear algebra), the method for solving for normal modes is not so clunky as it is shown to be here. Also, a deeper understanding of these modes becomes possible. As a quick preview of things to come, try the following:
- In the equations for the q's, treat the coefficients of the x's as though they are components of a vector.
- Take the dot product of the "vectors" q1 and q2. You will find that it vanishes for both of the examples above, and in fact this is a general feature of normal modes of all systems of oscillators.
This works no matter how many degrees of freedom are present – the 5 normal modes for a system of 5 blocks connected by springs form mutually-orthogonal 5-dimensional vectors. Indeed this mutual orthogonality is the origin of the use of the word "normal" in "normal modes."

