3.2: Position 4-Vector

World Lines as Vectors

World lines are collections of a continuous set of events in spacetime. Consider a straight world line that stretches from the origin to an event. This line has a magnitude (the spacetime interval between the origin and the event) and a direction (starting at the origin and ending at the event). We can therefore officially declare it to be a vector, and since it points from the origin and has units of length, it is a position vector. Clearly the magnitude of this position vector is quite different from others we have seen, thanks to the Minkowski "adjustment." Because this vector has four components (three for space and one for time), it is called the position 4-vector.

Figure 3.2.1 – Position 4-Vector of An Event

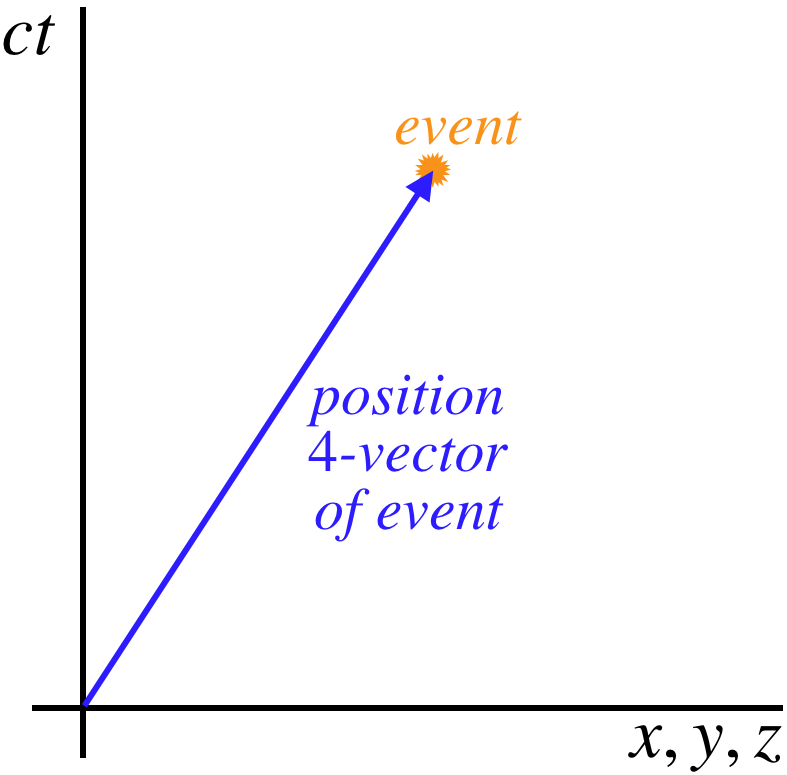
Traditionally, the components of this vector are expressed in a column matrix, with the time component being the first entry. [The entries of \(ct\), \(x\), \(y\) and \(z\) are typically numbered 0, 1, 2, and 3, respectively.] Another convention commonly followed is denoting a 4-vector with an upper-case letter (sometimes boldfaced) and no arrow over it, while 3-vectors (those we are accustomed to that exist in space without the time fourth dimension) are lower-case letters with the arrow above them. Here is a summary of conventions we will use here:

\[\text{position 4-vector:}\;\;\;\;\;X \leftrightarrow \left(\begin{array}{*{20}{c}} ct \\ x \\ y \\ z \end{array}\right) \text{ or } \left(\begin{array}{*{20}{c}} ct \\ \overrightarrow r \end{array}\right)\]

Alert

A note about the use of the double arrow rather than an equal sign in the expression above... The 4-vector of an event is an object that can be described by any of an infinite number of column matrices, depending upon the frame in which the components are measured. Therefore to call this vector "equal" to one specific set of components is not entirely accurate without somehow acknowledging the frame that that particular matrix represents. The double-arrow is a harmless-but-effective reminder of this important distinction between the 4-vector itself and its representation in a specific frame of reference. It is not "wrong" to use an equal sign (the distinction between the vector and its components is still implied), but we will use the double arrow here for pedagogical purposes.

Magnitude of the Position 4-Vector

Given what we already know about the length of world lines, we can make an important statement about the magnitude of the position 4-vector – it is equal to \(\Delta s\), which an invariant across inertial frames with coincident origins. This should not surprise us, as the event that it points to is agreed-upon by everyone.

We know that the square of the length of a vector is equal to the scalar product of the vector with itself, and applying that principle here shows us that we need to redefine how we do the scalar product. The usual "multiply like components and add the products" doesn't work, since the signs aren't right. Writing the scalar product in terms of matrices shows this:

\[X \cdot X = \left(ct \;\; x \;\; y \;\; z\right)\left(\begin{array}{*{20}{c}} ct \\ x \\ y \\ z \end{array}\right) = c^2t^2 + x^2 + y^2 + z^2 \ne \Delta s^2\]

We therefore make an adjustment to the definition of the spacetime scalar product of two vectors in matrix form by placing a square matrix between the vectors that takes care of the Minkowski metric:

\[X \cdot X = \left(ct \;\; x \;\; y \;\; z\right) \left(\begin{array}{*{20}{c}} 1 && 0 && 0 && 0 \\ 0 && -1 && 0 && 0 \\ 0 && 0 && -1 && 0 \\ 0 && 0 && 0 && -1 \end{array}\right) \left(\begin{array}{*{20}{c}} ct \\ x \\ y \\ z \end{array}\right) = c^2t^2 - x^2 - y^2 - z^2 = \Delta s^2\]

[The '\(\Delta\)' in \(\Delta s\) here represents the change from the origin, which is why there are no \(\Delta\)'s on the coordinates.]

Relating Two Frames

After our previous section on rotations, and showing here how the magnitude of the position 4-vector is invariant between frames of reference, it should be clear where we are going next. We already know that the orientation of a straight world line between two events is different in the spacetime diagrams of two different inertial observers (though it is a straight line in both frames), so we now make the claim that a Lorentz transformation linking two frames results in a sort of 4-dimensional "rotation" of the position vector.

Expressing this in matrix form is a simple matter of repeating the process we followed to get matrix Equation 3.1.6 from Equations 3.1.3, this time starting with Equations 2.2.9. The result is:

\[\left(\begin{array}{*{20}{c}} ct' \\ x' \\ y' \\ z' \end{array}\right) = \left(\begin{array}{*{20}{c}} \gamma_v && -\frac{v}{c}\gamma_v && 0 && 0 \\ -\frac{v}{c}\gamma_v && \gamma_v && 0 && 0 \\ 0 && 0 && 1 && 0 \\ 0 && 0 && 0 && 1 \end{array}\right) \left(\begin{array}{*{20}{c}} ct \\ x \\ y \\z \end{array}\right) \]

Thanks to the weirdness associated with including the time coordinate, this isn't exactly a rotation, as can be seen by comparing this equation to Equation 3.1.6, which has the two sine functions with different signs, while the corresponding elements in Lorentz transformation matrix have the same sign (not to mention the fact that the sine and cosine can never exceed a value of 1, while the corresponding elements in the Lorentz transformation matrix can and do exceed this value. Apparently "rotating" spatial coordinates into time coordinates (and vice-versa) is analogous to, but not quite the same as, rotating spatial coordinates into other spatial coordinates.