2.2: Lorentz Transformation
( \newcommand{\kernel}{\mathrm{null}\,}\)
Transformations Between Inertial Frames
When we first studied relative motion in Physics 9HA, we wrote down a way of translating between the values measured in the two frames. This set of equations was called the Galilean transformation equations. As sensible as these are, they clearly are not correct in light of what we now know about relativity. Most notably, the Galilean transformation assumes a universal time variable that is common to all frames.
So now we seek a new set of transformation equations to relate the spacetime coordinates of frames in relative motion. We will start with a couple of simplifying assumptions. First, the two frames in question share a spatial origin at the moment in time we will call t=t′=0 – we will define "event A" as occurring at this spacetime point. The effect of doing this is that distances and time intervals between this event and a second event are now just the spacetime coordinates themselves. For example: Δx=x−0=x and Δt′=t′−0=t′ .
For our second assumption, we will continue to define the relative motion as the primed frame moving at a speed v in the +x-direction relative to the unprimed frame.
In order to get a set of equations that gives us a translation between the (ct,x,y,z,) spacetime coordinates measured in one frame and the (ct′,x′,y′,z′,) spacetime coordinates measured in the other, we begin by noting that with motion only along the x-axis, the y and z coordinates will remain unchanged. For example, we know that lengths along those directions do not contract, so we would not expect the coordinates to be related in any way other than y′=y and z′=z. But what about the x and ct coordinates?
We start by assuming that the transformation is a linear one, not unlike the Galilean transformation (after all, the Galilean transformation does work for frames whose relative speed is low). This means that the primed values can be written as linear combinations of the unprimed values:
x′=J⋅x+K⋅ctct′=L⋅x+M⋅ct
Our goal is to determine the unknown constants J, K, L, and M that work for relativity. Let's start by defining "event B" viewed by the primed observer. Let's say that this event occurs at this observer's time t′, and takes place at the origin of the unprimed frame. Since the primed observer sees this frame moving in the −x′-direction for a time period of t′ after starting at the origin, the primed observer sees this event occur at the position x′=−vt′. Plugging x=0 (the event occurs at the unprimed origin) into the first equation above and comparing gives us the constant K:
x′=−vt′x′=0+K⋅ct}K=−(vc)(t′t)
Events A and B both occur at the origin of the unprimed frame, so the time span between them is the proper time, and the frame is inertial, so it is the spacetime interval. Therefore the time measured between these events in the primed and unprimed frames are related according to the usual time dilation formula:
t′=γvt
Plugging this in above gives us the constant K:
K=−(vc)γv
Using this same event B, we can obtain the constant M as well. Plugging in x=0 gives:
ct′=0+M⋅ct⇒M=t′t=γv
Recapping what we have so far:
x′=J⋅x−(vc)γvctct′=L⋅x+γvct
Now to determine the other two constants, define "event B" as occurring at the origin of the primed frame, x′=0. The unprimed observer will see this event occur at the position x=vt, which we can plug back in to get:
0=J⋅vt−γvvt⇒J=γv
To find the final constant L requires noting that the time measured in the primed frame for event B is now the proper time, and a bit more algebra than was needed for the previous constants (which is omitted here):
ct′=L⋅vt+γvctt=γvt′}L=−(vc)γv
Putting everything together gives us the Lorentz transformation equations:
ct′=γv[ct−(vc)x]x′=γv[x−(vc)ct]y′=yz′=z
The symmetry between the x and t variable is apparent, and shows the important difference between relativity and galilean physics – time is not universal and unaffected by the position of an event. Notice that when the velocity is very small compared to the speed of light (as it is in our everyday experience), then letting vc→0 changes the Lorentz transformation equations into the Galilean transformation equations.
Finally, it should be noted that these transformations can also be written in terms of changes in these variables from one event to another. In effect, this is hidden in the equations themselves, as event A simply has all the variables equal to zero.
These equations give the spacetime coordinates of an event in the primed frame given the spacetime coordinates of the same event in the unprimed frame. But what if we want to do the reverse – find the coordinates of the event in the unprimed frame from those in the primed frame? [This is called the inverse of this transformation.] It's actually quite easy to do – the only difference in perspectives between these two frames is the sign of the velocity. We get the inverse transformation by simply replacing the v everywhere in the equations with −v.
Example 2.2.1
We have said that the interval-squared Δs2=c2Δt2−Δx2−Δy2−Δz2 is an invariant, which means that it is the same in every inertial frame. Use the Lorentz transformation equations to show that this is true.
- Solution
-
We want to show that Δs′2=Δs2, which makes this a pure plug-in. Clearly the y and z changes are equal in both frames, so we will ignore them and deal with just the t and x changes:
Δs′2=c2Δt′2−Δx′2=(γv[cΔt−(vc)Δx])2−(γv[Δx−(vc)cΔt])2=γ2v[(c2Δt2−2vΔxΔt+v2c2Δx2)−(Δx2+2vΔxΔt+v2Δt2)]=γ2v[(1−v2c2)(c2Δt2−Δx2)]=Δs2
Revisiting Previous Results
After all that struggle with thought experiments and spacetime diagrams, only now do we have a simple, powerful tool for achieving the same results. Time dilation is downright trivial. If (unprimed) Ann sees two events occur at the same place (Δx=0) separated by a time interval Δt, then the time span that (primed) Bob measures between these events is:
cΔt′=γv[cΔt−(vc)Δx0]⇒Δt′=γvΔt
We can also look at simultaneity. Events that are simultaneous in Ann's frame (Δt=0) are not simultaneous in Bob's:
cΔt′=γv[cΔt0−(vc)Δx]≠0
Looking at this expression, we also see that Δt′ is negative (i.e. t2<t1) when Δx′ is positive (i.e. x2>x1). This means that for the two events that Ann sees as simultaneous, Bob sees the event with the greater x-value as occurring first (note that we are still assuming that Bob is moving in the +x-direction relative to Ann). So is Ann flies by Bob in a spaceship where she sees lights on the front and rear of her ship flashing in sync, Bob sees the light on the rear of her ship flashing ahead of the light on the front.
Reproducing length contraction is a bit more difficult to obtain from the Lorentz transformation equations. the reason is that the length that is measured by one observer depends upon different events than the length measured by the other observer. That is, the length of an object in a given frame is the distance between events located at both ends of the object that occur at the same time, and as just noted, events simultaneous in one frame are not simultaneous in the other. Nevertheless, we can get the length contraction result with some care.
Two events that are simultaneous at both ends of an object according to Bob gives:
0=cΔt′=γv[cΔt−vcΔx]⇒cΔt=vcΔx
Plugging this back into the transformation for the length measured by Bob gives the length contraction:
Δx′=γv[Δx−vΔt]=γv[Δx−v(vcΔx)]=γvΔx[1−v2c2]=Δxγv
Spacetime Diagrams with Two Observers
Whenever we compare what is seen by two observers in different reference frames, we do so by considering spacetime events, which are common to both. We also looked at how events can be expressed in a spacetime diagram in a specific frame. What we would like to do now is use a single spacetime diagram to depict how events are perceived in both frames at once.
To do this, we need to first choose one frame (we'll call it Ann's frame)to be the usual spacetime axes, then we need to plot the other frame's (Bob's) axes on that same diagram. This is not hard to do now that we have the lorentz transformation. We begin with the same assumption we made for the lorentz transformations – Ann and Bob have a common origin at time ct=ct′=0. This means that their spacetime axes have the same origin.
Next we'll plot Bob's time axis on Ann's spacetime diagram. But wait, what does "plot the time axis" mean? As we know already, even the time axis for Ann is a world line for an object at rest at the origin in Ann's frame. Bob's time axis represents the same thing – the world line of an object at rest at Bob's origin. We are assuming that Bob's frame is moving in the +x direction at a constant speed relative to Ann's frame, so Bob's time axis is a straight line starting at the origin with a slope of cv.
Figure 2.2.1 – Bob's Time Axis
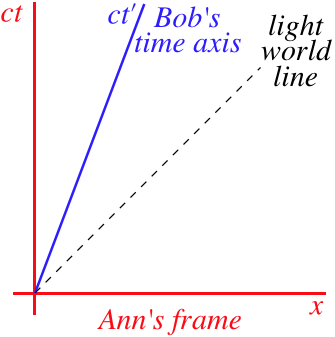
There is another way we can confirm this graph of Bob's time axis. The definition of anyone's time axis is the collection of points where the position on the x-axis remains a constant value of zero. If we plug x′=0 into the Lorentz transformation equations, we get:
0=γv[x−(vc)ct]⇒ct=(cv)x
So Bob's ct′ axis is a linear plot on Ann's axes (which are ct vs. x) intersecting with the origin with slope cv.
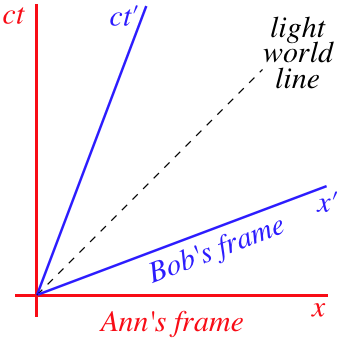
Okay, how do we plot Bob's x′ axis on Ann's spacetime diagram? The x′-axis isn't a world line (it has a slope less than that of light), so we can't use that argument again. We can throw together some logic for what the x′-axis should be, but it is simpler to use the lorentz transformation as we did in our confirmation of the time axis above. The x′-axis is defined as the set of points for which the time value ct′ remains a constant zero:
0=γv[ct−(vc)x]⇒ct=(vc)x
So Bob's x′-axis is a line on Ann's spacetime diagram that passes through the origin with a slope of vc. This is simply the line that is symmetrically-placed across the time world line from the ct′-axis:
Figure 2.2.2 – Bob's Frame in Ann's Spacetime Diagram
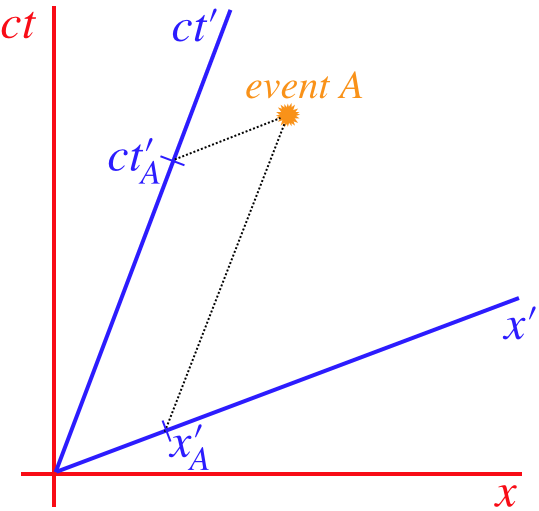
We know how to get the time and space coordinates using Ann's axes, but how do we do it with Bob, when the axes are not mutually perpendicular? Well, the points that make up Bob's time axis are the world line of an object at rest at the origin. An object at rest at x′=1m will be moving at the same speed in Ann's frame as the object at the origin, so it's world line will be parallel to the ct′ axis. This means that we can find the x′ position of an event by tracing a path back to the x′-axis parallel to the ct′ axis. Similarly, the ct′ coordinate can be found by tracing a straight line from the event parallel to the x′ axis back to the ct′ axis.
Figure 2.2.3 – An Event Recorded in Bob's Frame
It is important to note that the scaling of the unprimed and primed axes in this diagram are not equal. Keeping in mind that the ct′-axis is the world line of the primed frame's origin represented in the unprimed frame, then if we pick a point on the ct′-axis, the value of Δs from the origin to that point is the same for both frames. This means that the tick marks representing fixed units of distances on the primed frame are farther apart than those on the unprimed frame. Let's look at an example to make this clear:
Suppose the primed frame is moving at 0.8c relative to the unprimed frame. Then the slope of the ct′-axis is 54. Let's look at a point on the ct′-axis that is 4 units over on the x-axis from the origin, and 5 units up the ct-axis. This point on the ct′-axis needs to be marked Δs=√52−42= 3 units. So the tick-mark for 3 units on the ct′-axis is farther from the origin than the tick-mark for 5 units on the ct-axis is from the origin.
With this graphical tool, we can demonstrate all the previous results we have obtained – some easily, some with difficulty. Perhaps the easiest is simultaneity. Place any two events that are simultaneous in one of the two frames, and it becomes immediately apparent that they cannot be simultaneous in the other. What is more, it also clear which of the two events comes first in the frame in which they are not simultaneous.
The invariance of the speed of light is another result that is easy to see, at least for light traveling in the +x direction. The world line of a light beam moving in the +x direction must have a slope of +1, which needs to split both pairs of axes. For light traveling in the −x direction, it is not immediately obvious that the two axes again share the same world line. But extend the v=−c world line until it hits both axes, and it is easy to see that in both cases it intersects the same values on the ct and x-axes in both frames (it is perpendicular to the v=+c world line, so the symmetry is clear).


