6.4: Conversion Between Equatorial and Altazimuth Coordinates
- Page ID
- 6822
Whereabouts in the sky will a given star be at a certain time? This as a typical problem involving conversion between equatorial and altazimuth coordinates. We have to solve a spherical triangle. That is no problem – we already know how to do that. The problem is: which triangle?
The first problem, however, arises from the phrase “at a certain time”. In particular, if we want to know where a star is, for example, at 2002 November 24, at 10:00 p.m. Pacific Standard Time as seen from Victoria, whose longitude is \(123^\circ \ 25^\prime.0 \ \text{W}\), we need to know the local sidereal time at that instant.
The calculation might go something like this.
From the Astronomical Almanac we find that the local sidereal times at Greenwich at \(0^\text{h}\) \(\text{UT}\) on November 25 and 26, 2002, are
November 25: \(04^\text{h} \ 16^\text{m} 59^\text{s}\)
November 26: \(04 \ \ \ 20 \ \ \ 56\)
We want the local sidereal time at November \(24^\text{d} \ 22^\text{h} \ 00^\text{m} \ \text{PST}\)
= November \(25^\text{d} \ 06^\text{h} \ 00^\text{m} \ \text{UT}\)
By interpolation we find that the local sidereal time at Greenwich at that instant is \(10^\text{h} \ 17^\text{m} \ 58^\text{s}\) .
The longitude of Victoria is \(08^\text{h} \ 13^\text{m} \ 40^\text{s}\) , and therefore the local sidereal time at Victoria is \(02^\text{h} \ 04^\text{m} \ 18^\text{s}\) .
We have overcome the first obstacle, and we now know the local sidereal time (LST).
We’ll ask ourselves now what are the altitude and azimuth of a star whose right ascension and declination are \(α\) and \(δ\). We also need the latitude of the observer (= altitude of the north celestial pole), which I’ll call \(\phi\). The hour angle \(H\) of the star is \(\text{LST}\) − \(α\).
The triangle that we have to solve is the triangle \(\text{PZX}\). Here \(\text{P}\), \(\text{Z}\) and \(\text{X}\) are, respectively, the north celestial pole, the zenith and the star. That is, we solve the triangle formed by the star and the poles of the two coordinate systems of interest. I draw the celestial sphere in figure \(\text{VI.3}\) as seen from the west. I have marked in the hour angle \(H\), the codeclination \(90^\circ\) − \(δ\), the altitude \(\phi\) of the pole, the zenith distance \(z\) and the azimuth \(A\) measured from the north point westwards.
In triangle \(\text{PZX}\), we know \(\phi\), \(δ\) and \(H\), so we immediately find the zenith distance \(z\) by application of the cosine formula (equation 3.5.2) and the azimuth \(A\) from the cotangent formula (equation 3.5.5).
Problem. Show that the hour angle \(H\) of a star of declination \(δ\) when it sets for an observer at latitude \(\phi\) is given by \(\cos H = − \tan δ \tan \phi\). This will enable you now to find the Local Sidereal Time of starset, since \(\text{LST} = \text{hour angle plus right ascension}\), and then you can convert to your zone solar time.
Show also that the azimuth \(\text{A}\) of starset, westward from the north point, is given by \(\tan A = − \sin \phi \tan H\).
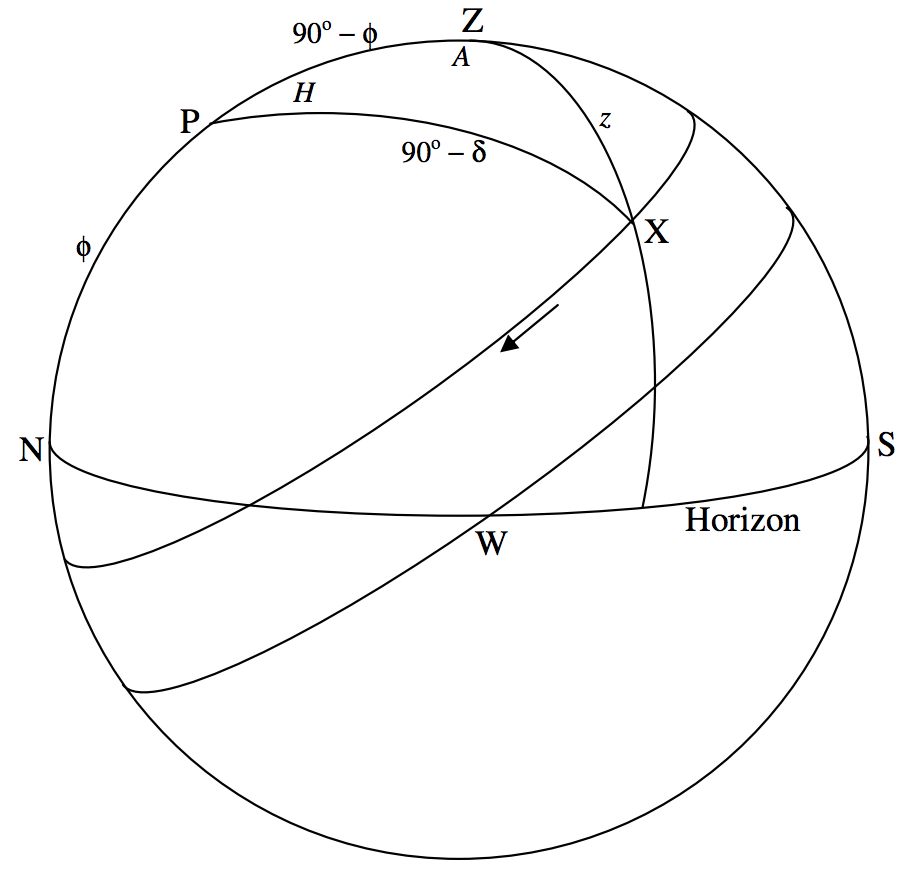
\(\text{FIGURE VI.3}\)