6.5: Ecliptic Coordinates
- Page ID
- 6823
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
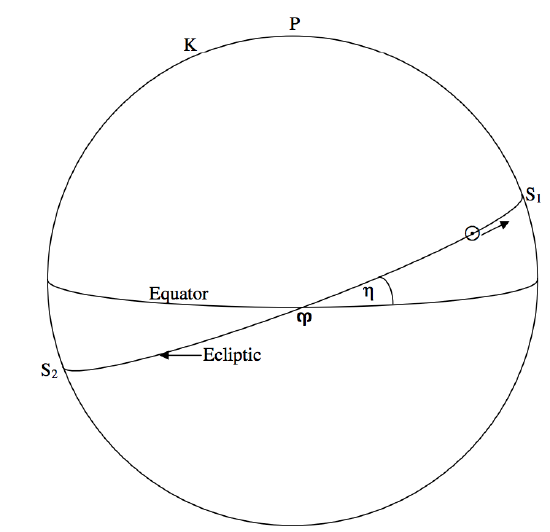
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In figures \(\text{VI.2}\) and \(\text{3}\) we were concerned mainly with the daily rotation of the celestial sphere. In figure \(\text{VI.4}\) we shall be concerned mainly with the annual motion of the Sun relative to the stars on the celestial sphere. In contrast to figures \(\text{VI.2}\) and 3, I have drawn the celestial equator, not the observer’s horizon, horizontally, and the north celestial pole, not the observer’s zenith, is at the top of the diagram. It is found that, for an observer on Earth, the Sun moves eastward relative to the stars during the course of the year, its right ascension continuously increasing; this apparent motion of the Sun relative to the stars is, of course, a consequence of the Earth revolving around the Sun.
\(\text{FIGURE VI.4}\)
Relative to the stars, it is found that, during the course of a year, the Sun moves eastward along a great circle that is inclined to the equator at an angle of about \(23^\circ .4\). This great circle is called the ecliptic, and it is the projection of the plane of Earth’s orbit on the celestial sphere. The angle between the ecliptic and the equator is called the Obliquity of the Ecliptic. The ecliptic crosses the equator at two points. The Sun reaches one of these points on about March 22 each year on its way north at which time the Sun’s declination changes from negative to positive. This point, the ascending node of the Sun’s path on the equator, is the First Point of Aries, which we introduced in Section 6.3. As mentioned there, and for reasons that will be explained in section 6.7, it is actually in the constellation Pisces rather than Aries. Nevertheless it is still known as the First Point of Aries and is denoted by the astrological symbol \(\Upsilon\) for Aries. It is the point from which right ascensions are measured. The instant of time when the Sun crosses the equator from north to south at the First Point of Aries is the March Equinox. Days and nights are of equal length all over the world on that date (“equinox” = “equal night”), and that date marks the first day of Spring in the northern hemisphere. For that reason it is also called the “vernal equinox” (Latin verna = “spring”) – but that is hardly fair to southern hemisphere astronomers, for it marks the beginning of the southern autumn.
About three months later, on or near June 21, the Sun reaches the point \(S_1\) at the June Solstice (called by those who live in the Northern hemisphere, the summer solstice). The declination of the Sun is then at its highest point, \(+23.4\) degrees. At that instant the rate of change of the Sun’s declination is zero, which explains the origin of the word “solstice”, which implies that the Sun is momentarily standing still. The Sun is then in the constellation Gemini. After a further three months, the Sun has descended back to the equator on its way south, at the September equinox (the “autumnal equinox” for northerners) on or near September 23, when the Sun is in the constellation Virgo. And after a further three months the Sun reaches its most southerly declination at the December solstice (“winter solstice” to northerners) on or near December 21, when the Sun is in the constellation Sagittarius.
Also drawn in figure \(\text{VI.4}\) is the North Pole of the Ecliptic, \(\text{K}\), which is in Draco. The South Pole of the Ecliptic is in Dorado.
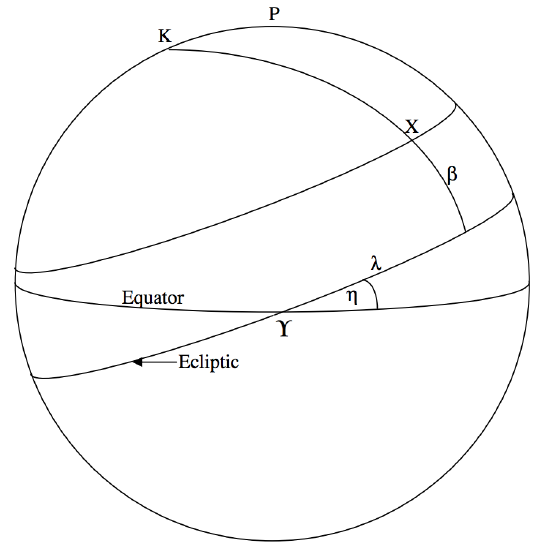
The ecliptic and its pole K form the basis of the ecliptic coordinate system, illustrated in figure \(\text{VI.5}\). The ecliptic longitude \(λ\) and the ecliptic latitude \(β\) of a star \(\text{X}\) are shown in figure \(\text{VI.5}\), which should be self explanatory. In order to convert between equatorial and ecliptic coordinates, the triangle to solve is triangle \(\text{PKX}\). The arc \(\text{KX}\) is \(90^\circ − β\) and the angle \(\text{PKX}\) is \(90^\circ − λ\). What are the arc \(\text{PK}\), the arc \(\text{PX}\) and the angle \(\text{KPX}\)?
[Answers: \(\text{PK} = η\) \(\text{PX} = 90^\circ − δ\) \(\text{KPX} = 90^\circ + α]\)
\(\text{FIGURE VI.5}\)


