7.21: Zeeman effect
- Page ID
- 8922
When a hot gas which is emitting or absorbing spectrum lines is placed in a magnetic field, the lines become split into several components. This is known as the Zeeman effect, discovered in 1896 by the Dutch spectroscopist P. Zeeman.
If we start by thinking of an atom with zero nuclear spin, it will be recalled that every energy level except those with \(J = 0\) is degenerate. That is, there are \(2J + 1\) wavefunctions, or eigenstates, or just states, each described by a quantum number \(M\), which goes from \(−J\) to \(+J\), and each of these states has exactly the same energy. When the atom is placed in an external magnetic field, this degeneracy is removed, and each state has a slightly different energy. This happens to both levels involved in the formation of a line (unless one of the levels has \(J = 0\)), with the result that the line that joins the two levels is split up into a number of components. It will be recalled that a line joins two levels. In a similar manner a (Zeeman) component joins two states. Just as a multiplet is the totality of lines joining two terms, so a line is the totality of components joining two levels. In the absence of a magnetic field, all the states within a level have the same energy, and all the components that make up a line have the same wavelength. A term is described by \(LS\). Its multiplicity is \(2 \text{min} \left\{ L , S \right\} +1\) and its statistical weight is \((2L +1)( 2S +1)\). A level is described by \(LSJ\). Its degeneracy and statistical weight are \(2J + 1\). A state is described by \(LSJM\). It is not degenerate; its statistical weight is \(1\).
In sections 9 ,10, and 11 of this chapter, I went to some trouble to persuade you that an electron is not a hard, spinning sphere that moves in a circular orbit around a nucleus. Rather I described electrons in terms of wavefunctions that describe the probability amplitude, and quantum numbers were eigenvalues of certain operators and were restricted to certain values as a result of boundary conditions. What model we use to describe the behaviour of atoms depends on our purpose, and, if our purpose was to obtain expertise in the intricacies of quantum mechanical calculations, we would have to become heavily involved in the algebra of kets, operators and eigenfunctions. Our present purpose, however, is to become acquainted in a rather descriptive way with spectroscopy, and in describing Zeeman phenomena without the intention of performing quantum mechanical calculations. It will be convenient to revert to a model of an electron, if not as a hard, spinning, orbiting particle, at least as an entity that possesses the attributes of orbital and spin angular momentum and consequently also of magnetic moment.
In particular, we recall that an orbiting electron has an orbital angular momentum \(\sqrt{l(l +1)}\hbar\), where \(\hbar=h/(2\pi )\) has the value \(1.055 \times 10^{−34} \text{J s}\). Now, if we take the magnetogyric ratio of an orbiting electron to be \(e/ (2m)\), the magnetic moment of an orbiting electron is \(\sqrt{l(l+1)}\cdot \dfrac{e \hbar}{2m}\). (Those who object to this simple treatment - and there are some rather obvious objections - will have no alternative but to do a proper quantum mechanical derivation, though the result is the same.) In any case, the quantity \(\dfrac{e\hbar}{2m}\), a unit of magnetic moment, is called the Bohr magneton, and its value is \(9.274 \times 10^{−24} \ \text{N m T}^{−1}\) or \(\text{A m}^2\). I shall use the symbol \(\mu_B\) to indicate the Bohr magneton. Thus the orbital angular momentum of an electron is \(\sqrt{l(l +1)}\hbar\) and its magnetic moment is \(\sqrt{l(l+1)}\mu_B\) The magnetogyric ratio of an orbiting electron (not taking into account the contribution to angular momentum and magnetic moment from its spin) is \(\mu_B / \hbar = e/ (2m) = 8.794 \times 10^{10} \ \text{C kg}^{-1}\), or, if we agree to express angular momentum in units of \(\hbar\) and magnetic moment in units of Bohr magnetons, the magnetogyric ratio of an orbiting electron (still taking no account of the contributions of spin) is \(1\). The spin angular momentum of an electron is \(\sqrt{s(s+1)}\hbar\), where \(s =1/2\), and its magnetic moment is (very close to) \(2\sqrt{s(s+1)}\hbar\), so that its magnetogyric ratio is just \(e/m\), or, in units of \(\mu\) and \(\hbar\), it is \(2\). (The exact value of the magnetogyric ratio, in units of \(\mu_B / \hbar\), is a little more than \(2\), and is one of the most precisely-known of the fundamental physical constants. Its value in the year 2000 is given as 2.002 319 304 374.)
In discussion of the Zeeman effect, we shall need to know the magnetogyric ratio of the atom in a given level, since this determines the way in which the levels are split in a magnetic field. The ratio of the magnetic moment in units of \(\mu_B\) to the angular momentum in units of \(\hbar\) is known as the Landé splitting factor, and is generally denoted by the symbol \(g\). It is the magnetogyric ratio in units of \(e/(2m)\), or \(8.794 \times 10^{10} \ \text{C kg}^{-1}\). The magnetogyric ratio, or Landé splitting factor, of an atom in a given level depends on the angle between the vectors \(\textbf{L}\) and \(\textbf{S}\) and hence on their resultant \(\textbf{J}\), and , though I do not do it here, it is not difficult to show that, in the case of \(LS\)-coupling, the Landé splitting factor has the value
\[g = 1 + \dfrac{J(J+1) + S(S+1) - L(L+1)}{2J(J+1)}. \label{7.21.1} \tag{7.21.1}\]
(This formula is calculated using the approximate value \(2\) for the magnetogyric ratio of the electron rather than the more accurate \(2.00232\). More accurately, it should be written
\[g = 1 + 1.00232 \dfrac{J(J+1)+S(S+1)-L(L+1)}{2J(J+1)}. \label{7.21.2} \tag{7.21.2}\]
Formulas for the \(g\)-factor for other coupling schemes are available, but I do not give them here, since in practice the coupling between electron angular momenta in complex atoms is usually intermediate between idealized extremes, and the calculation has to be done numerically. In many of the lightest atoms, however, pure \(LS\)-coupling is a good approximation. The \(g\)-value can be found experimentally from observations of the Zeeman effect, and, in addition to Landé's interval rule mentioned earlier, this affords another good indication of how close a level is to \(LS\)-coupling.
Problem. The \(^5 \text{P}_1 - \ ^5 \text{D}_0^\text{o}\) line of \(\text{Fe}_\text{ I}\) at \(617.33 \ \text{nm}\) is often used to investigate magnetic fields in sunspots. The strongest line of the multiplet that includes this line is \(^5\text{P}_3 - \ ^5 \text{D}_4^\text{o}\). Calculate the \(g\)-factor for each of the four levels mentioned.
A small point to be made is as follows. From what we have said, the magnetic moment of an atom (excluding nuclear spin, if any) is of magnitude \(\mu = g\mu_B \sqrt{J (J +1)}\). (This follows from the definition of \(g\), which is the ratio of the magnetic moment in units of the Bohr magneton - i.e. \(\mu/\mu_B\) - to the angular momentum in units of \(\hbar\).) In vector form this must be written \(\boldsymbol{\mu} = −g \mu_B \textbf{J}\), where \(\textbf{J}\) is a dimensionless vector of magnitude \(\sqrt{J(J +1)}\) and the minus sign arises because of the negative electron charge, the magnetic moment and angular momentum vectors being oppositely directed.
When the Zeeman effect was first investigated, lines were observed to be split into just three components, and this was referred to as the normal Zeeman effect. Later, more complex patterns were observed, and this was referred to as the anomalous Zeeman effect. As we now understand it, the so-called "normal" Zeeman effect is merely the Zeeman effect observed on lines joining levels with spin \(S = 0\), which have a simpler Zeeman pattern than other lines. In addition to the Stern-Gerlach experiment, it was the study of "anomalous" Zeeman splitting that gave rise to the discovery of electron spin.
We are now in a position to start looking at how energy levels are split in the presence of a magnetic field. Let us consider, for example, a \(^1 \text{P}_1\) level (\(L, \ S, \ J = 1, 0, 1\)). The Landé factor is \(1\). (Note that for any level in which S = 0 and therefore in which \(J\) and \(L\) are necessarily equal, Equation \(\ref{7.21.1}\) (or \ref{7.21.2}) shows that \(g = 1\).)
The magnetic moment is \(\boldsymbol{\mu} = −g \mu_B \textbf{J} = −\mu_B \textbf{J}\). The energy of a magnet is a magnetic field is \(−\boldsymbol{\mu} \cdot \textbf{B}\), so in this case it is \(\mu_B \textbf{J}\cdot \textbf{B}\). But \(\textbf{J}\cdot \textbf{B}\) is equal to \(B\) times the component of \(\textbf{J}\) in the direction of \(\textbf{B}\), which is \(M\). Thus the energy of the state \(M\) in the magnetic field is \(\mu_B MB\). There are three values of \(M \ (−1, \ 0, \ 1)\). The splitting of the level into its three states is linearly proportional to the magnetic field \(B\), and the separation between adjacent states is \(\mu_B B\).
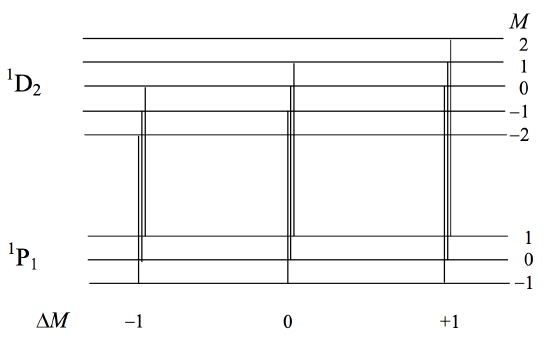
If we consider a \(^1 \text{D}_2\) level, again \(g = 1\), and the states have just the same spacing, except that this time there are five states, with \(M = −2 \) to \(+2\).
Now consider the line \(^1 \text{P}_1 − \ ^1 \text{D}_2\). This is the totality of all transitions connecting the three states in the one to the five states in the other. Not all transitions are possible, however, so there are not fifteen components to the line. Selection rules (to be dealt with in Section 7.24) limit the only possible transitions to those for which \(\Delta M = 0\) or \(\pm 1\). Figure VII.1 shows the energy levels of the eight states and the nine possible transitions that connect them.
It will be seen that the nine components are in three groups of three, and that, because the spacings in the two levels are the same (which in turn is a result of \(S = 0\)), all three lines in a given group have exactly the same wavelength (although I have drawn them slightly separated). Consequently, you will see in the spectrum apparently only three Zeeman components, the full
\(\text{FIGURE VII.1}\)
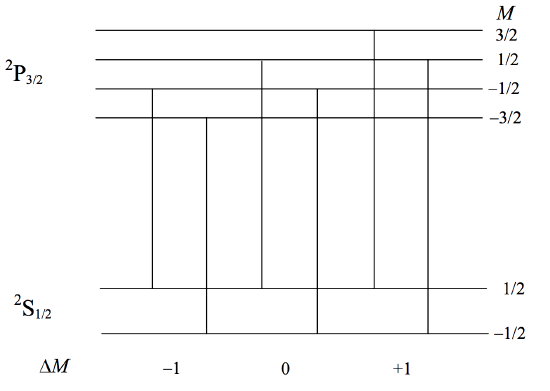
nine not being completely separated. This is what was called the "normal" Zeeman effect. However, as soon as \(S \neq 0\), the \(g\)-values of the two levels will be different, spacings of the states in the two levels will be different, all the components will be fully separated, and we see the "anomalous" Zeeman effect, although there is nothing really at all anomalous about it. In a sense, the "normal" Zeeman effect is exceptional. In figure \(\text{VII.2}\) I have drawn, schematically (with wavelength increasing linearly to the right), the Zeeman pattern for \(^2 \text{S}_{\dfrac{1}{2}} - \ ^2 \text{P}_{\dfrac{3}{2}}\). The splitting factors for the \(\text{P}\) and \(\text{S}\) levels are, respectively, \(2\) and \(4/3\). It happens that in this case all six Zeeman components are equally spaced, though this is not always the case; the exact pattern of Zeeman components varies from line to line
\(\text{FIGURE VII.2}\)


