13.10: The Transformer

We met the transformer briefly in Section 10.9. There we pointed out that the EMF induced in the secondary coil is equal to the number of turns in the secondary coil times the rate of change of magnetic flux; and the flux is proportional to the EMF applied to the primary times the number of turns in the primary. Hence we deduced the well known relation

$$\tag{13.10.1}\dfrac{V_2}{V_1}=\dfrac{N_2}{N_1}$$

relating the primary and secondary voltages to the number of turns in each. We now look at the transformer in more detail; in particular, we look at what happens when we connect the secondary coil to a circuit and take power from it.

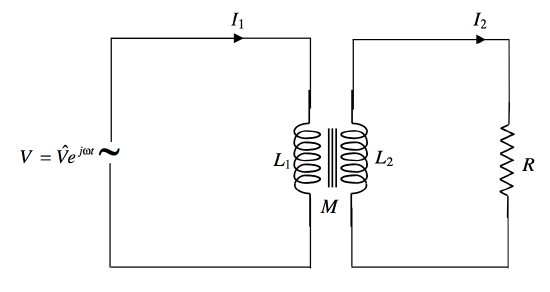
Figure $\text{XIII.12}$

In Figure $\text{XIII.12}$, we apply an AC EMF $V=\hat{V}e^{j\omega t}$ to the primary circuit. The self inductance of the primary coil is $L_1$, and an alternating current $I_1$ flows in the primary circuit. The self inductance of the secondary coil is $L_2$, and the mutual inductance of the two coils is $M$. If the coupling between the two coils is very tight, then $M=\sqrt{L_1L_2}$; otherwise it is less than this. I am supposing that the resistance of the primary circuit is much smaller than the reactance, so I am going to neglect it.

The secondary coil is connected to a resistance $R$. An alternating current $I_2$ flows in the secondary circuit.

Let us apply Ohm's law (or Kirchhoff's second rule) to each of the two circuits.

In the primary circuit, the applied EMF V is opposed by two back EMF's:

$$\tag{13.10.2}V=L_1\dot I_1 +M\dot I_2.$$

That is to say

$$\tag{13.10.3}V=j\omega L_1 I_1 +j\omega MI_2.$$

Similarly for the secondary circuit:

$$\tag{13.10.4}0=j\omega MI_1+j\omega L_2I_2+RI_2.$$

These are two simultaneous equations for the currents, and we can (with a small effort) solve them for $I_1$ and $I_2$:

$$\label{13.10.5}\tag{13.10.5}\left [ \dfrac{RL_1}{M}+j\left (\dfrac{\omega L_1L_2}{M}-\omega M \right )\right ]I_1=\left (\dfrac{L_2}{M}-j\dfrac{R}{\omega M}\right )V$$

and

$$\tag{13.10.6}\left [R+j\left ( \omega L_2-\dfrac{\omega M^2}{L_1}\right ) \right ]I_2=-\dfrac{MV}{L_1}.$$

This would be easier to understand if we were to do the necessary algebra to write these in the forms $I_1=(a+jb)V\text{ and }I_2=(c+jd)V$. We could then easily see the phase relationships between the current and $V$ as well as the peak values of the currents. There is no reason why we should not try this, but I am going to be a bit lazy before I do it, and I am going to assume that we have a well designed transformer in which the secondary coil is really tightly wound around the primary, and $M=\sqrt{L_1L_2}$ If you wish, you may carry on with a less efficient transformer, with $M=k\sqrt{L_1L_2}$ where $k$ is a coupling coefficient less than 1, but I'm going to stick with $M=\sqrt{L_1L_2}$. In that case, Equations $\ref{13.10.5}$ and 6 eventually take the forms

$$\tag{13.10.7}I_1=\left ( \dfrac{L_2}{L_1R}-j\dfrac{1}{L_1\omega}\right ) V = \left ( \dfrac{N_2^2}{N_1^2R}-j\dfrac{1}{L_1\omega}\right )V$$

and

$$\label{13.10.8}\tag{13.10.8}I_2=-\dfrac{1}{R}\sqrt{\dfrac{L_2}{L_1}}V=-\dfrac{N_2}{N_1R}V.$$

These equations will tell us, on examination, the magnitudes of the currents, and their phases relative to $V$.

Now look at the circuit shown in Figure $\text{XIII.13}$.

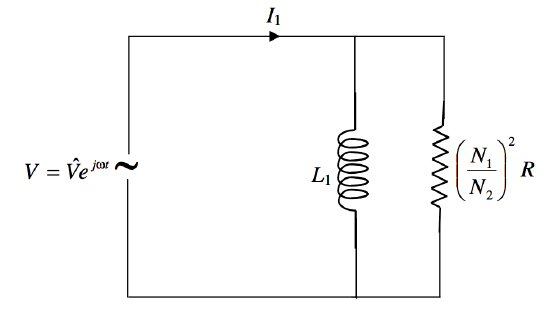
Figure $\text{XIII.13}$

In Figure $\text{XIII.13}$ we have a resistance $R(N_1/N_2)^2$ in parallel with an inductance $L_1$. The admittances of these two elements are, respectively, $(N_2/N_1)^2/R$ and $-j/(L_1\omega)$, so the total admittance is $\dfrac{N_2^2}{N_1^2R}-j\dfrac{1}{L_1\omega}$. Thus, as far as the relationship between current and voltage is concerned, the primary circuit of the transformer is precisely equivalent to the circuit drawn in Figure $\text{XIII.13}$. To see the relationship between $I_1$ and $V$, we need look no further than Figure $\text{XIII.13}$.

Likewise, Equation $\ref{13.10.8}$ shows us that the relationship between $I_2$ and $V$ is exactly as if we had an AC generator of EMF $N_2V/N_1$ connected across $R$, as in Figure $\text{XIII.14}$.

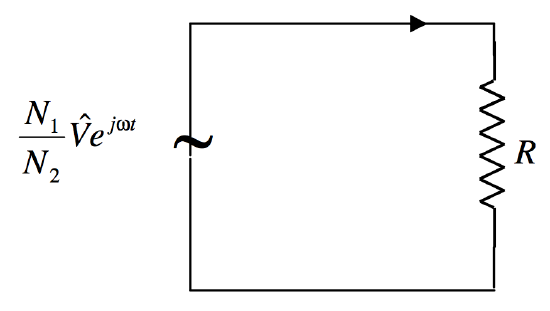
Figure $\text{XIII.14}$

Note that, if the secondary is short-circuited (i.e. if $R = 0$ and if the resistance of the secondary coil is literally zero) both the primary and secondary current become infinite. If the secondary circuit is left open (i.e. $R = \infty$), the secondary current is zero (as expected), and the primary current, also as expected, is not zero but is $-jV/(L_1\omega)$; That is to say, the current is of magnitude $V/(L_1\omega)$ and it lags behind the voltage by 90^o, just as if the secondary circuit were not there.