7.5: Magnetic Moment of a Plane, Current-carrying Coil

A plane, current carrying coil also experiences a torque in an external magnetic field, and its behaviour in a magnetic field is quite similar to that of a bar magnet or a compass needle. The torque is maximum when the normal to the coil is perpendicular to the 3 magnetic field, and the magnetic moment is defined in exactly the same way, namely the maximum torque experienced in unit magnetic field.

Let us examine the behavior of a rectangular coil of sides a and b, which is free to rotate about the dashed line shown in Figure $\text{VII.2}$.

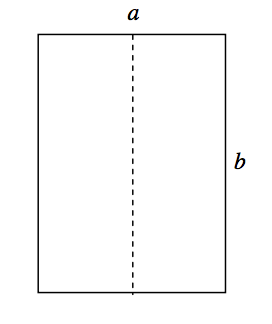
$\text{FIGURE VII.2}$

In Figure $\text{VII.3}$, I am looking down the axis represented by the dashed line in Figure $\text{VII.2}$, and we see the coil sideways on. A current $I$ is flowing around the coil in the directions indicated by the symbols $\bigodot$ and $\bigotimes$. The normal to the coil makes an angle $\theta$ with respect to an external field $B$.

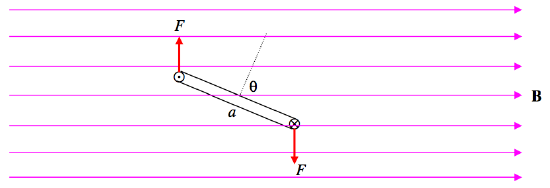
$\text{FIGURE VII.3}$

According to the Biot-Savart law there is a force $F$ on each of the b-length arms of magnitude $bIB$, or, if there are $N$ turns in the coil, $F = NbIB$. These two forces are opposite in direction and constitute a couple. The perpendicular distance between the two forces is $a \sin θ$, so the torque $\tau$ on the coil is $NabIB \sin θ$, or $\tau = NAIB \sin θ$, where $A$ is the area of the coil. This has its greatest value when $\theta = 90^\circ$, and so the magnetic moment of the coil is $NIA$. This shows that, in SI units, magnetic moment can equally well be expressed in units of $\text{A m}^2$, or ampere metre squared, which is dimensionally entirely equivalent to $\text{N m T}^{−1}$. Thus we have

$$\tau = p_mB\sin \theta,$$

where, for a plane current-carrying coil, the magnetic moment is

$$p_m = NIA.$$

This can conveniently be written in vector form:

$$\tau=\textbf{p}_m \times \textbf{B},$$

where, for a plane current-carrying coil,

$$\textbf{p}_m = NI\textbf{A}.$$

Here $\textbf{A}$ is a vector normal to the plane of the coil, with the current flowing clockwise around it. The vector $\tau$ is directed into the plane of the paper in Figure $\text{VII.3}$

The formula $NIA$ for the magnetic moment of a plane current-carrying coil is not restricted to rectangular coils, but holds equally for plane coils of any shape; for (see Figure $\text{VII.4}$) any curve can be described in terms of an infinite number of infinitesimally small vertical and horizontal segments.

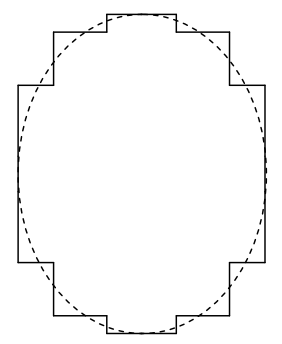
$\text{FIGURE VII.4}$

We understand that a magnet, or anything that has a magnetic moment, experiences no net force in a uniform magnetic field, although it does experience a torque. Furthermore, as in the case of an electric dipole in an electric field, a magnetic dipole situated in an inhomogeneous magnetic field does experience a net force. If the magnetic moment and the gradient of the magnetic field are in the same direction, the net force on the dipole is

$$\nonumber p_m\frac{dB}{dx}.$$

[$\text{N m T}^{-1} \times \text{T m}^{-1} = \text{N}.$]

See Section 3.5 for further details relating to a dipole in an inhomogeneous field.

An important historical experiment that readers may come across, using the force on a magnetic dipole in an inhomogeneous magnetic field, is the 1922 experiment of Stern and Gerlach, demonstrating the spatial quantization of the magnetic moment associated with electron spin.