9.3: Transformations between CM and lab frame
- Page ID
- 15054
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Even though the use of the invariant mass simplifies calculations considerably, it clearly does not provide all necessary information. It does suggest however, that a natural frame to analyze reactions is the center of mass (CM) frame. Often we shall analyze a process in this frame, and use a Lorentz transformation to get information about processes in the laboratory frame. Since almost all processes involve the scattering (deflection) of one particle by another (or a number of others), this is natural example for such a procedure, see the sketch in Figure \(\PageIndex{1}\). The same procedure can also be applied to the case of production of particles, such as the annihilation process discussed above.
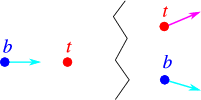
Before the collision the beam particle moves with four-momentum \[p_b=(p_{\mathrm{lab}},0,0,\sqrt{m_b^2 c^4+p_{\mathrm{lab}}^2c^2}) \nonumber \] and the target particle \(m_t\) is at rest, \[p_t=(0,0,0,m_t c^2). \nonumber \] We first need to determine the velocity \(v\) of the Lorentz transformation that bring is to the centre-of-mass frame. We use the Lorentz transformation rules for momenta to find that in a Lorentz frame moving with velocity \(v\) along the \(x\)-axis relative to the CM frame we have \[\begin{aligned} p'_{bx} &=& \gamma(v) (p_{\mathrm{lab}}- v E_{\mathrm{lab}}/c^2) \nonumber\\ p'_{tx} &=& -m_t v \gamma(v).\end{aligned} \nonumber \] Sine in the CM frame these numbers must be equal in size but opposite in sign, we find a linear equation for \(v\), with solution \[v = \frac{p_{\mathrm{lab}}}{m_t+E_{\mathrm{lab}}/c^2} \approx c\left(1-\frac{m_t}{p_{\mathrm{lab}}}\right). \nonumber \] Now if we know the momentum of the beam particle in the CM frame after collision, \[(p_f\cos\theta_{\mathrm{CM}},p_f\sin\theta_{\mathrm{CM}},0,E'_f), \nonumber \] where \(\theta_{\mathrm{CM}}\) is the CM scattering angle we can use the inverse Lorentz transformation, with velocity \(-v\), to try and find the lab momentum and scattering angle, \[\begin{aligned} \gamma(v)(p_f\cos\theta_{\mathrm{CM}} +vE'_f/c^2) &=& p_{f\mathrm{lab}} \cos\theta_{\mathrm{lab}}\nonumber \\ p_f\sin\theta_{\mathrm{CM}} &=& p_{f\mathrm{lab}} \sin\theta_{\mathrm{lab}},\end{aligned} \nonumber \] from which we conclude \[\tan\theta_{\mathrm{lab}} = \frac{1}{\gamma(v)}\frac{p_f \sin \theta_{\mathrm{CM}}}{p_f \cos\theta_{\mathrm{CM}} +v E'_f/c^2}. \nonumber \] Of course in experimental situations we shall often wish to transform from lab to CM frames, which can be done with equal ease.
To understand some of the practical consequences we need to look at the ultra-relativistic limit, where \(p_{\mathrm{lab}} \gg m/c\). In that case \(v\approx c\), and \(\gamma(v) \approx (p_{\mathrm{lab}}/2m_t c^2)^{1/2}\). This leads to \[\tan \theta_{\mathrm{lab}} \approx \sqrt{\frac{2m_t c^2}{p_{\mathrm{lab}}}} \frac{u \sin \theta_C}{u\cos\theta_C+c} \nonumber \] Here \(u\) is the velocity of the particle in the CM frame. This function is always strongly peaked in the forward direction unless \(u \approx c\) and \(\cos\theta_C\approx -1\).


