10.8: Medical Applications and Biological Effects of Nuclear Radiation
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe two medical uses of nuclear technology
- Explain the origin of biological effects due to nuclear radiation
- List common sources of radiation and their effects
- Estimate exposure for nuclear radiation using common dosage units
Nuclear physics is an integral part of our everyday lives (Figure \PageIndex{1}). Radioactive compounds are used in to identify cancer, study ancient artifacts, and power our cities. Nuclear fusion also powers the Sun, the primary source of energy on Earth. The focus of this chapter is nuclear radiation. In this section, we ask such questions as: How is nuclear radiation used to benefit society? What are its health risks? How much nuclear radiation is the average person exposed to in a lifetime?
Medical Applications
Medical use of nuclear radiation is quite common in today’s hospitals and clinics. One of the most important uses of nuclear radiation is the location and study of diseased tissue. This application requires a special drug called a radiopharmaceutical. A radiopharmaceutical contains an unstable radioactive isotope. When the drug enters the body, it tends to concentrate in inflamed regions of the body. (Recall that the interaction of the drug with the body does not depend on whether a given nucleus is replaced by one of its isotopes, since this interaction is determined by chemical interactions.) Radiation detectors used outside the body use nuclear radiation from the radioisotopes to locate the diseased tissue. Radiopharmaceuticals are called radioactive tags because they allow doctors to track the movement of drugs in the body. Radioactive tags are for many purposes, including the identification of cancer cells in the bones, brain tumors, and Alzheimer’s disease (Figure \PageIndex{2}). Radioactive tags are also used to monitor the function of body organs, such as blood flow, heart muscle activity, and iodine uptake in the thyroid gland.
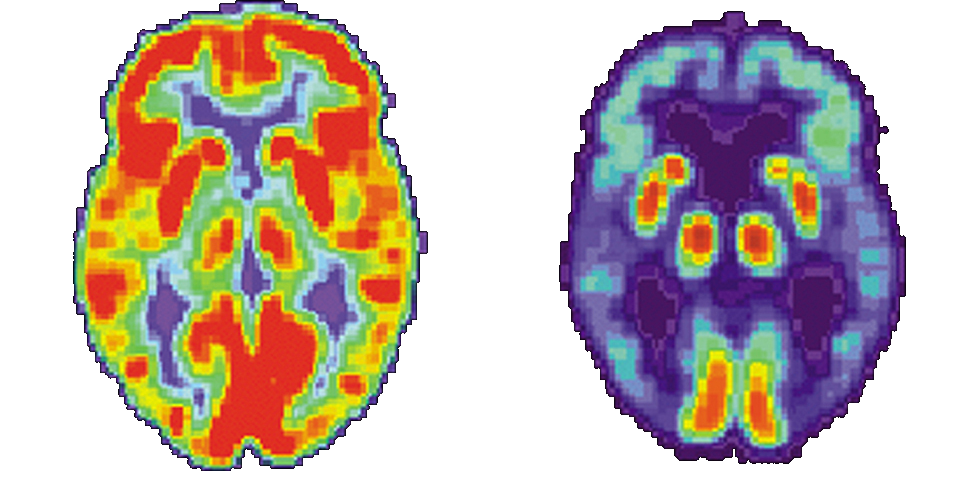
Table \PageIndex{1} lists some medical diagnostic uses of radiopharmaceuticals, including isotopes and typical activity (A) levels. One common diagnostic test uses iodine to image the thyroid, since iodine is concentrated in that organ. Another common nuclear diagnostic is the thallium scan for the cardiovascular system, which reveals blockages in the coronary arteries and examines heart activity. The salt TlCl can be used because it acts like NaCl and follows the blood. Note that Table \PageIndex{1} lists many diagnostic uses for ^{99m}Tc, where “m” stands for a metastable state of the technetium nucleus. This isotope is used in many compounds to image the skeleton, heart, lungs, and kidneys. About 80\% of all radiopharmaceuticals employ ^{99m}Tc because it produces a single, easily identified, 0.142-MeV \gamma ray and has a short 6.0-h half-life, which reduces radiation exposure.
| Procedure, Isotope | Activity (mCi), where 1mCi = 3.7 \times 10^7 Bq | Procedure, Isotope | Activity (mCi), where 1mCi = 3.7 \times 10^7 Bq |
|---|---|---|---|
| Brain scan | Thyroid scan | ||
| ^{99m}Tc | 7.5 | ^{131}I | 0.05 |
| ^{15}O (PET) | 50 | ^{123}I | 0.07 |
| Lung scan | Liver scan | ||
| ^{133}Xe | 7.5 | ^{198}Au colloid | 0.1 |
| ^{99m}Tc | 2 | ^{99m}Tc | 2 |
| Cardiovascular blood pool | Bone scan | ||
| ^{131}I | 0.2 | ^{85}Sr | 0.1 |
| ^{99m}Tc | 2 | ^{99m}Tc | 10 |
| Cardiovascular arterial flow | Kidney scan | ||
| ^{201}Tl | 3 | ^{197}Hg | 0.1 |
| ^{24}Na | 7.5 | ^{99m}Tc | 1.5 |
Diagnostic Uses of Radiopharmaceuticals
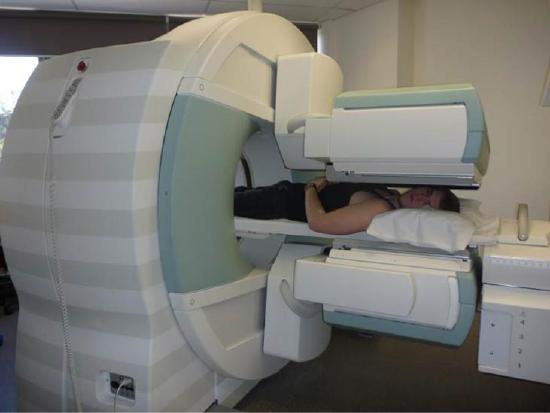
The first radiation detectors produced two-dimensional images, like a photo taken from a camera. However, a circular array of detectors that can be rotated can be used to produce three-dimensional images. This technique is similar to that used in X-ray computed tomography (CT) scans. One application of this technique is called single-photon-emission CT (SPECT) (Figure \PageIndex{3}). The spatial resolution of this technique is about 1 cm.
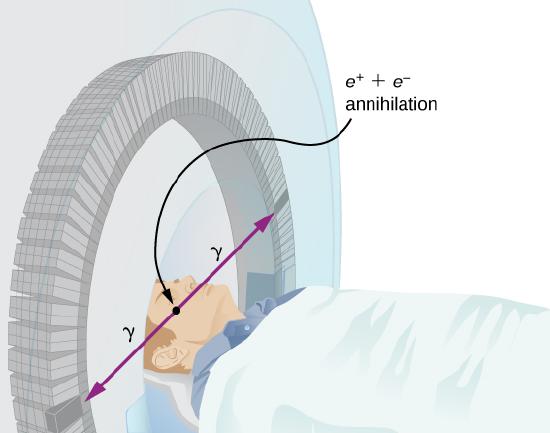
Improved image resolution is achieved by a technique known as positron emission tomography (PET). This technique use radioisotopes that decay by \beta^+ radiation. When a positron encounters an electron, these particle annihilate to produce two gamma-ray photons. This reaction is represented by
e^+ + e^- \rightarrow 2\gamma. \nonumber
These \gamma-ray photons have identical 0.511-MeV energies and move directly away from one another (Figure \PageIndex{4}). This easily identified decay signature can be used to identify the location of the radioactive isotope. Examples of \beta^+-emitting isotopes used in PET include ^{11}C, {13}N, ^{15}O, and ^{18}F. The nuclei have the advantage of being able to function as tags for natural body compounds. Its resolution of 0.5 cm is better than that of SPECT.
PET scans are especially useful to examine the brain’s anatomy and function. For example, PET scans can be used to monitor the brain’s use of oxygen and water, identify regions of decreased metabolism (linked to Alzheimer’s disease), and locate different parts of the brain responsible for sight, speech, and fine motor activity
Is it a tumor? View an animation of simplified magnetic resonance imaging (MRI) to see if you can tell. Your head is full of tiny radio transmitters (the nuclear spins of the hydrogen nuclei of your water molecules). In an MRI unit, these little radios can be made to broadcast their positions, giving a detailed picture of the inside of your head.
Biological Effects
Nuclear radiation can have both positive and negative effects on biological systems. However, it can also be used to treat and even cure cancer. How do we understand these effects? To answer this question, consider molecules within cells, particularly DNA molecules.
Cells have long, double-helical DNA molecules containing chemical codes that govern the function and processes of the cell. Nuclear radiation can alter the structural features of the DNA chain, leading to changes in the genetic code. In human cells, we can have as many as a million individual instances of damage to DNA per cell per day. DNA contains codes that check whether the DNA is damaged and can repair itself. This repair ability of DNA is vital for maintaining the integrity of the genetic code and for the normal functioning of the entire organism. It should be constantly active and needs to respond rapidly. The rate of DNA repair depends on various factors such as the type and age of the cell. If nuclear radiation damages the ability of the cell to repair DNA, the cell can
- Retreat to an irreversible state of dormancy (known as senescence);
- Commit suicide (known as programmed cell death); or
- Progress into unregulated cell division, possibly leading to tumors and cancers.
Nuclear radiation can harm the human body is many other ways as well. For example, high doses of nuclear radiation can cause burns and even hair loss.
Biological effects of nuclear radiation are expressed by many different physical quantities and in many different units. A common unit to express the biological effects of nuclear radiation is the rad or radiation dose unit. One rad is equal to 1/100 of a joule of nuclear energy deposited per kilogram of tissue, written:
1 \, rad = 0.01 \, J/kg. \nonumber
For example, if a 50.0-kg person is exposed to nuclear radiation over her entire body and she absorbs 1.00 J, then her whole-body radiation dose is
(1.00 \, J)/(50.0 \, kg) = 0.0200 \, J/kg = 2.00 \, rad. \nonumber
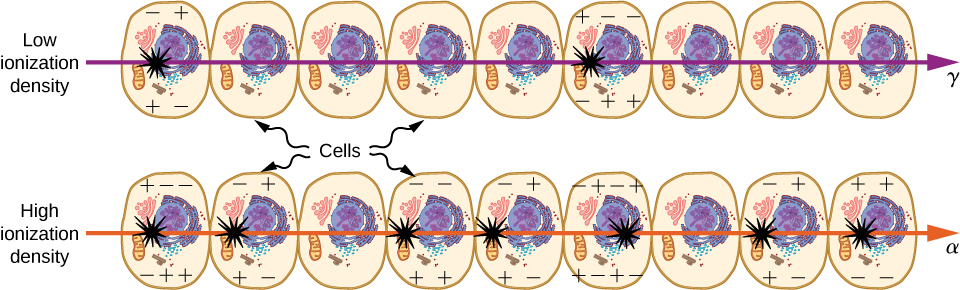
Nuclear radiation damages cells by ionizing atoms in the cells as they pass through the cells (Figure \PageIndex{5}). The effects of ionizing radiation depend on the dose in rads, but also on the type of radiation (alpha, beta, gamma, or X-ray) and the type of tissue. For example, if the range of the radiation is small, as it is for \alpha rays, then the ionization and the damage created is more concentrated and harder for the organism to repair. To account for such affects, we define the relative biological effectiveness (RBE). Sample RBE values for several types of ionizing nuclear radiation are given in Table \PageIndex{2}.
| Type and Energy of Radiation | RBE[1] |
|---|---|
| X-rays | 1 |
| \gamma-rays | 1 |
| \beta rays greater than 32 keV | 1 |
| \beta rays less than 32 keV | 1.7 |
| Neutrons, thermal to slow (<20 keV) | 2 - 5 |
| Neutrons, fast (1–10 MeV) | 10 (body), 32 (eyes) |
| Protons (1–10 MeV) | 10 (body), 32 (eyes) |
| rays from radioactive decay | 10–20 |
| Heavy ions from accelerators | 10–20 |
| [1] Values approximate. Difficult to determine. | |
A dose unit more closely related to effects in biological tissue is called the roentgen equivalent man (rem) and is defined to be the dose (in rads) multiplied by the relative biological effectiveness (RBE). Thus, if a person had a whole-body dose of 2.00 rad of \gamma radiation, the dose in rem would be (2.00 \, rad)(1) = 2.00 rem for the whole body. If the person had a whole-body dose of 2.00 rad of \alpha radiation, then the dose in rem would be (2.00 \, rad)(20) = 40.0 rem for the whole body. The \alpha rays would have 20 times the effect on the person than the \gamma rays for the same deposited energy. The SI equivalent of the rem, and the more standard term, is the sievert (Sv) is
1 \, Sv = 100 \, rem. \nonumber
The RBEs given in Table \PageIndex{3} are approximate but reflect an understanding of nuclear radiation and its interaction with living tissue. For example, neutrons are known to cause more damage than \gamma rays, although both are neutral and have large ranges, due to secondary radiation. Any dose less than 100 mSv (10 rem) is called a low dose, 0.1 Sv to 1 Sv (10 to 100 rem) is called a moderate dose, and anything greater than 1 Sv (100 rem) is called a high dose. It is difficult to determine if a person has been exposed to less than 10 mSv.
Biological effects of different levels of nuclear radiation on the human body are given in Table \PageIndex{3} The first clue that a person has been exposed to radiation is a change in blood count, which is not surprising since blood cells are the most rapidly reproducing cells in the body. At higher doses, nausea and hair loss are observed, which may be due to interference with cell reproduction. Cells in the lining of the digestive system also rapidly reproduce, and their destruction causes nausea. When the growth of hair cells slows, the hair follicles become thin and break off. High doses cause significant cell death in all systems, but the lowest doses that cause fatalities do so by weakening the immune system through the loss of white blood cells.
| Dose in Sv[1] | Effect |
|---|---|
| 0–0.10 | No observable effect. |
| 0.1–1 | Slight to moderate decrease in white blood cell counts. |
| 0.5 | Temporary sterility; 0.35 for women, 0.50 for men. |
| 1–2 | Significant reduction in blood cell counts, brief nausea and vomiting. Rarely fatal. |
| 2–5 | Nausea, vomiting, hair loss, severe blood damage, hemorrhage, fatalities. |
| 4.5 | Lethal to 50\% of the population within 32 days after exposure if not treated. |
| 5–20 | Worst effects due to malfunction of small intestine and blood systems. Limited survival. |
| >20 | Fatal within hours due to collapse of central nervous system. |
[1] Multiply by 100 to obtain dose in rem.
Sources of Radiation
Human are also exposed to many sources of nuclear radiation. A summary of average radiation doses for different sources by country is given in Table \PageIndex{4}. Earth emits radiation due to the isotopes of uranium, thorium, and potassium. Radiation levels from these sources depend on location and can vary by a factor of 10. Fertilizers contain isotopes of potassium and uranium, which we digest in the food we eat. Fertilizers have more than 3000 Bq/kg radioactivity, compared to just 66 Bq/kg for Carbon-14.
| Source | Dose (mSv/y)[1] | |||
|---|---|---|---|---|
| Australia | Germany | US | World | |
| Natural radiation – external | ||||
| Cosmic rays | 0.30 | 0.28 | 0.30 | 0.39 |
| Soil, building materials | 0.40 | 0.40 | 0.30 | 0.48 |
| Radon gas | 0.90 | 1.1 | 2.0 | 1.2 |
| Natural radiation – internal | ||||
| ^{40}K, {14}C, ^{226}Ra | 0.24 | 0.28 | 0.40 | 0.29 |
| Artificial radiation | ||||
| Medical and dental | 0.80 | 0.90 | 0.53 | 0.40 |
| TOTAL | 2.6 | 3.0 | 3.5 | 2.8 |
| [1] Multiply by 100 to obtain does in mrem/y. | ||||
Medical visits are also a source of nuclear radiation. A sample of common nuclear radiation doses is given in Table \PageIndex{5}. These doses are generally low and can be lowered further with improved techniques and more sensitive detectors. With the possible exception of routine dental X-rays, medical use of nuclear radiation is used only when the risk-benefit is favorable. Chest X-rays give the lowest doses—about 0.1 mSv to the tissue affected, with less than 5\% scattering into tissues that are not directly imaged. Other X-ray procedures range upward to about 10 mSv in a CT scan, and about 5 mSv (0.5 rem) per dental X-ray, again both only affecting the tissue imaged. Medical images with radiopharmaceuticals give doses ranging from 1 to 5 mSv, usually localized.
| Procedure | Effective Dose (mSv) |
|---|---|
| Chest | 0.02 |
| Dental | 0.01 |
| Skull | 0.07 |
| Leg | 0.02 |
| Mammogram | 0.40 |
| Barium enema | 7.0 |
| Upper GI | 3.0 |
| CT head | 2.0 |
| CT abdomen | 10.0 |
The Chernobyl accident in Ukraine (formerly in the Soviet Union) exposed the surrounding population to a large amount of radiation through the decay of^{137}Cs. The initial radioactivity level was approximately A = 6.0 \, MCi. Calculate the total mass of^{137}Cs involved in this accident.
Strategy
The total number of nuclei, N, can be determined from the known half-life and activity of ^{137}Cs (30.2 y). The mass can be calculated from N using the concept of a mole.
Solution
Solving the equation A = \frac{0.693 \, N}{t_{1/2}} for N gives
N = \frac{At_{1/2}}{0.693}. \nonumber
Entering the given values yields
N = \frac{(6.0 \, MCi)(30.2\, y)}{0.693}. \nonumber
To convert from curies to becquerels and years to seconds, we write
N = \frac{(6.0 \times 10^6 \, Ci)(3.7 \times 10^{10} Bq/Ci) (30.2 \, y)(3.16 \times 10^7 \, s/y)}{0.693} = 3.1 \times 10^{26} \nonumber
One mole of a nuclide ^AX has a mass of A grams, so that one mole of ^{137}Cs has a mass of 137 g. A mole has 6.02 \times 10^{23} nuclei. Thus the mass of ^{137}Cs released was
\[m = \left(\frac{137 \, g}{6.02 \times 10^{23}\right)(3.1 \times 10^{26}) = 70 \times 10^3 \, g = 70 \, kg. \nonumber \]
Significance
The mass of \ce{^{137}Cs} involved in the Chernobyl accident is a small material compared to the typical amount of fuel used in a nuclear reactor. However, approximately 250 people were admitted to local hospitals immediately after the accident, and diagnosed as suffering acute radiation syndrome. They received external radiation dosages between 1 and 16 Sv. Referring to biological effects in Table \PageIndex{3}, these dosages are extremely hazardous. The eventual death toll is estimated to be around 4000 people, primarily due to radiation-induced cancer.
Radiation propagates in all directions from its source, much as electromagnetic radiation from a light bulb. Is activity concept more analogous to power, intensity, or brightness?
- Answer
-
power


