7.3: The Heisenberg Uncertainty Principle
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Describe the physical meaning of the position-momentum uncertainty relation
- Explain the origins of the uncertainty principle in quantum theory
- Describe the physical meaning of the energy-time uncertainty relation
Heisenberg’s uncertainty principle is a key principle in quantum mechanics. Very roughly, it states that if we know everything about where a particle is located (the uncertainty of position is small), we know nothing about its momentum (the uncertainty of momentum is large), and vice versa. Versions of the uncertainty principle also exist for other quantities as well, such as energy and time. We discuss the momentum-position and energy-time uncertainty principles separately.
Momentum and Position
To illustrate the momentum-position uncertainty principle, consider a free particle that moves along the x-direction. The particle moves with a constant velocity u and momentum p=mu. According to de Broglie’s relations, p=ℏk and E=ℏω. As discussed in the previous section, the wavefunction for a free particle is given by
ψk(x,t)=A[cos(ωt−kx)−isin(ωt−kx)]=Ae−i(ωt−kx)=Ae−i(ωt−kx)=Ae−iωteikx
and the probability density |ψk(x,t)|2=A2 is uniform and independent of time. The particle is equally likely to be found anywhere along the x-axis but has definite values of wavelength and wave number, and therefore momentum. The uncertainty of position is infinite (we are completely uncertain about position) and the uncertainty of the momentum is zero (we are completely certain about momentum). This account of a free particle is consistent with Heisenberg’s uncertainty principle.
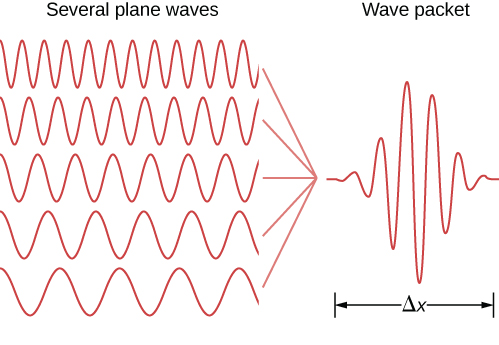
Similar statements can be made of localized particles. In quantum theory, a localized particle is modeled by a linear superposition of free-particle (or plane-wave) states called a wave packet. An example of a wave packet is shown in Figure 7.3.1. A wave packet contains many wavelengths and therefore by de Broglie’s relations many momenta—possible in quantum mechanics! This particle also has many values of position, although the particle is confined mostly to the interval Δx. The particle can be better localized (Δx can be decreased) if more plane-wave states of different wavelengths or momenta are added together in the right way (Δp is increased). According to Heisenberg, these uncertainties obey the following relation.
The product of the uncertainty in position of a particle and the uncertainty in its momentum can never be less than one-half of the reduced Planck constant:
ΔxΔp≥ℏ2.
This relation expresses Heisenberg’s uncertainty principle. It places limits on what we can know about a particle from simultaneous measurements of position and momentum. If Δx is large, Δp is small, and vice versa. Equation ??? can be derived in a more advanced course in modern physics. Reflecting on this relation in his work The Physical Principles of the Quantum Theory, Heisenberg wrote “Any use of the words ‘position’ and ‘velocity’ with accuracy exceeding that given by [the relation] is just as meaningless as the use of words whose sense is not defined.”
Note that the uncertainty principle has nothing to do with the precision of an experimental apparatus. Even for perfect measuring devices, these uncertainties would remain because they originate in the wave-like nature of matter. The precise value of the product ΔxΔp depends on the specific form of the wavefunction. Interestingly, the Gaussian function (or bell-curve distribution) gives the minimum value of the uncertainty product:
ΔxΔp=ℏ2
Determine the minimum uncertainties in the positions of the following objects if their speeds are known with a precision of 1.0×10−3m/s:
- an electron and
- a bowling ball of mass 6.0 kg.
Strategy
Given the uncertainty in speed Δu=1.0×10−3m/s, we have to first determine the uncertainty in momentum Δp=mΔu and then invert Equation ??? to find the uncertainty in position
Δx=ℏ2Δp.
Solution
- For the electron: Δp=mΔu=(9.1×10−31kg)(1.0×10−3m/s)=9.1×10−34kg⋅m/s, Δx=ℏ2Δp=5.8cm.
- For the bowling ball: Δp=mΔu=(6.0kg)(1.0×10−3m/s)=6.0×10−3kg⋅m/s, Δx=ℏ2Δp=8.8×10−33m.
Significance
Unlike the position uncertainty for the electron, the position uncertainty for the bowling ball is immeasurably small. Planck’s constant is very small, so the limitations imposed by the uncertainty principle are not noticeable in macroscopic systems such as a bowling ball.
Estimate the ground-state energy of a hydrogen atom using Heisenberg’s uncertainty principle. (Hint: According to early experiments, the size of a hydrogen atom is approximately 0.1 nm.)
Strategy
An electron bound to a hydrogen atom can be modeled by a particle bound to a one-dimensional box of length L=0.1nm. The ground-state wavefunction of this system is a half wave. This is the largest wavelength that can “fit” in the box, so the wavefunction corresponds to the lowest energy state. Note that this function is very similar in shape to a Gaussian (bell curve) function. We can take the average energy of a particle described by this function (E) as a good estimate of the ground state energy (E0). This average energy of a particle is related to its average of the momentum squared, which is related to its momentum uncertainty.
Solution
To solve this problem, we must be specific about what is meant by “uncertainty of position” and “uncertainty of momentum.” We identify the uncertainty of position (Δx) with the standard deviation of position (σx), and the uncertainty of momentum (Δp) with the standard deviation of momentum (σp). For the Gaussian function, the uncertainty product is
σxσp=ℏ2,
where
σ2x=x2−¯x2
and
σ2p=p2−¯p2.
The particle is equally likely to be moving left as moving right, so ¯p2=0. Also, the uncertainty of position is comparable to the size of the box, so σx=L. The estimated ground state energy is therefore
E0=EGaussian=¯p2m=σ2p2m=12m(ℏ2σx)2=12m(ℏ2L)2=ℏ28mL2.
E0=(ℏc)28(mc2)L2=(197.3eV⋅nm)28(0.511⋅106eV)(0.1nm)2=0.952eV≈1eV.
Multiplying numerator and denominator by c2 gives
Significance
Based on early estimates of the size of a hydrogen atom and the uncertainty principle, the ground-state energy of a hydrogen atom is in the eV range. The ionization energy of an electron in the ground-state energy is approximately 10 eV, so this prediction is roughly confirmed. (Note: The product ℏcℏc is often a useful value in performing calculations in quantum mechanics.)
Energy and Time
Another kind of uncertainty principle concerns uncertainties in simultaneous measurements of the energy of a quantum state and its lifetime,
ΔEΔt≥ℏ2
where ΔE is the uncertainty in the energy measurement and Δt is the uncertainty in the lifetime measurement. The energy-time uncertainty principle does not result from a relation of the type expressed by Equation ??? for technical reasons beyond this discussion. Nevertheless, the general meaning of the energy-time principle is that a quantum state that exists for only a short time cannot have a definite energy. The reason is that the frequency of a state is inversely proportional to time and the frequency connects with the energy of the state, so to measure the energy with good precision, the state must be observed for many cycles.
To illustrate, consider the excited states of an atom. The finite lifetimes of these states can be deduced from the shapes of spectral lines observed in atomic emission spectra. Each time an excited state decays, the emitted energy is slightly different and, therefore, the emission line is characterized by a distribution of spectral frequencies (or wavelengths) of the emitted photons. As a result, all spectral lines are characterized by spectral widths. The average energy of the emitted photon corresponds to the theoretical energy of the excited state and gives the spectral location of the peak of the emission line. Short-lived states have broad spectral widths and long-lived states have narrow spectral widths.
An atom typically exists in an excited state for about Δt=10−8s. Estimate the uncertainty Δf in the frequency of emitted photons when an atom makes a transition from an excited state with the simultaneous emission of a photon with an average frequency of f=7.1×1014Hz. Is the emitted radiation monochromatic?
Strategy
We invert Equation ??? to obtain the energy uncertainty ΔE≈ℏ/2Δt and combine it with the photon energy E=hf to obtain Δf. To estimate whether or not the emission is monochromatic, we evaluate Δf/f.
Solution
The spread in photon energies is ΔE=hΔf. Therefore,
ΔE≈ℏ2Δt⇒hΔt≈ℏ2Δt⇒Δf≈14πΔt=14π(10−8s)=8.0×106Hz,
Δff=8.0×106Hz7.1×1014Hz=1.1×10−8.
Significance
Because the emitted photons have their frequencies within 1.1×10−6 percent of the average frequency, the emitted radiation can be considered monochromatic.
A sodium atom makes a transition from the first excited state to the ground state, emitting a 589.0-nm photon with energy 2.105 eV. If the lifetime of this excited state is 1.6×10−8s, what is the uncertainty in energy of this excited state? What is the width of the corresponding spectral line?
- Answer
-
4.1×10−8eV; 1.1×10−5nm


