16.6: The Electromagnetic Spectrum
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Explain how electromagnetic waves are divided into different ranges, depending on wavelength and corresponding frequency
- Describe how electromagnetic waves in different categories are produced
- Describe some of the many practical everyday applications of electromagnetic waves
Electromagnetic waves have a vast range of practical everyday applications that includes such diverse uses as communication by cell phone and radio broadcasting, WiFi, cooking, vision, medical imaging, and treating cancer. In this module, we discuss how electromagnetic waves are classified into categories such as radio, infrared, ultraviolet, and so on. We also summarize some of the main applications for each range.
The different categories of electromagnetic waves differ in their wavelength range, or equivalently, in their corresponding frequency ranges. Their properties change smoothly from one frequency range to the next, with different applications in each range. A brief overview of the production and utilization of electromagnetic waves is found in Table 16.6.1.
| Type of wave | Production | Applications | Issues |
|---|---|---|---|
| Radio | Accelerating charges | Communications, Remote controls, MRI | Requires control for band use |
| Microwaves | Accelerating charges and thermal agitation | Communications, Ovens, Radar, Cell phone use | |
| Infrared | Thermal agitation and electronic transitions | Thermal imaging, Heating | Absorbed by atmosphere, Greenhouse effect |
| Visible light | Thermal agitation and electronic transitions | Photosynthesis, Human vision | |
| Ultraviolet | Thermal agitation and electronic transitions | Sterilization, Vitamin D production | Ozone depletion, Cancer causing |
| X-rays | Inner electronic transitions and fast collisions | Security, Medical diagnosis, Cancer therapy | Cancer causing |
| Gamma rays | Nuclear decay | Nuclear medicine, Security, Medical diagnosis, Cancer therapy | Cancer causing, Radiation damage |
The relationship c=fλ between frequency f and wavelength λ applies to all waves and ensures that greater frequency means smaller wavelength. Figure 16.6.2 shows how the various types of electromagnetic waves are categorized according to their wavelengths and frequencies - that is, it shows the electromagnetic spectrum.

Radio Waves
The term radio waves refers to electromagnetic radiation with wavelengths greater than about 0.1 m. Radio waves are commonly used for audio communications (i.e., for radios), but the term is used for electromagnetic waves in this range regardless of their application. Radio waves typically result from an alternating current in the wires of a broadcast antenna. They cover a very broad wavelength range and are divided into many subranges, including microwaves, electromagnetic waves used for AM and FM radio, cellular telephones, and TV signals.
There is no lowest frequency of radio waves, but ELF waves, or “extremely low frequency” are among the lowest frequencies commonly encountered, from 3 Hz to 3 kHz. The accelerating charge in the ac currents of electrical power lines produce electromagnetic waves in this range. ELF waves are able to penetrate sea water, which strongly absorbs electromagnetic waves of higher frequency, and therefore are useful for submarine communications.
In order to use an electromagnetic wave to transmit information, the amplitude, frequency, or phase of the wave is modulated, or varied in a controlled way that encodes the intended information into the wave. In AM radio transmission, the amplitude of the wave is modulated to mimic the vibrations of the sound being conveyed. Fourier’s theorem implies that the modulated AM wave amounts to a superposition of waves covering some narrow frequency range. Each AM station is assigned a specific carrier frequency that, by international agreement, is allowed to vary by ±5kHz. In FM radio transmission, the frequency of the wave is modulated to carry this information, as illustrated in Figure 16.6.2, and the frequency of each station is allowed to use 100 kHz on each side of its carrier frequency. The electromagnetic wave produces a current in a receiving antenna, and the radio or television processes the signal to produce the sound and any image. The higher the frequency of the radio wave used to carry the data, the greater the detailed variation of the wave that can be carried by modulating it over each time unit, and the more data that can be transmitted per unit of time. The assigned frequencies for AM broadcasting are 540 to 1600 kHz, and for FM are 88 MHz to108 MHz.

Cell phone conversations, and television voice and video images are commonly transmitted as digital data, by converting the signal into a sequence of binary ones and zeros. This allows clearer data transmission when the signal is weak, and allows using computer algorithms to compress the digital data to transmit more data in each frequency range. Computer data as well is transmitted as a sequence of binary ones and zeros, each one or zero constituting one bit of data.
Microwaves
Microwaves are the highest-frequency electromagnetic waves that can be produced by currents in macroscopic circuits and devices. Microwave frequencies range from about 109Hz to nearly 1012Hz. Their high frequencies correspond to short wavelengths compared with other radio waves—hence the name “microwave.” Microwaves also occur naturally as the cosmic background radiation left over from the origin of the universe. Along with other ranges of electromagnetic waves, they are part of the radiation that any object above absolute zero emits and absorbs because of thermal agitation, that is, from the thermal motion of its atoms and molecules.
Most satellite-transmitted information is carried on microwaves. Radar is a common application of microwaves. By detecting and timing microwave echoes, radar systems can determine the distance to objects as diverse as clouds, aircraft, or even the surface of Venus.
Microwaves of 2.45 GHz are commonly used in microwave ovens. The electrons in a water molecule tend to remain closer to the oxygen nucleus than the hydrogen nuclei (Figure 16.6.3). This creates two separated centers of equal and opposite charges, giving the molecule a dipole moment. The oscillating electric field of the microwaves inside the oven exerts a torque that tends to align each molecule first in one direction and then in the other, with the motion of each molecule coupled to others around it. This pumps energy into the continual thermal motion of the water to heat the food. The plate under the food contains no water, and remains relatively unheated.
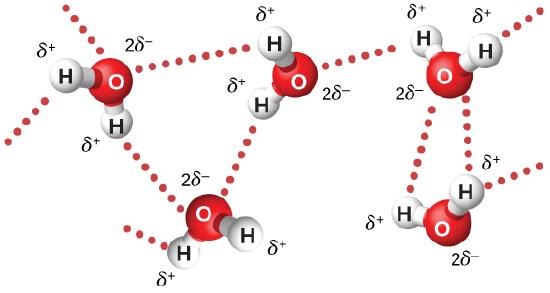
The microwaves in a microwave oven reflect off the walls of the oven, so that the superposition of waves produces standing waves, similar to the standing waves of a vibrating guitar or violin string (Normal Modes of a Standing Sound Wave). A rotating fan acts as a stirrer by reflecting the microwaves in different directions, and food turntables, help spread out the hot spots.
How far apart are the hotspots in a 2.45-GHz microwave oven?
Strategy
Consider the waves along one direction in the oven, being reflected at the opposite wall from where they are generated.
Solution
The antinodes, where maximum intensity occurs, are half the wavelength apart, with separation
d=12λ=12cf=3.00×108m/s2(2.45×109Hz)=6.02cm.
Significance
The distance between the hot spots in a microwave oven are determined by the wavelength of the microwaves.
A cell phone has a radio receiver and a weak radio transmitter, both of which can quickly tune to hundreds of specifically assigned microwave frequencies. The low intensity of the transmitted signal gives it an intentionally limited range. A ground-based system links the phone to only to the broadcast tower assigned to the specific small area, or cell, and smoothly transitions its connection to the next cell when the signal reception there is the stronger one. This enables a cell phone to be used while changing location.
Microwaves also provide the WiFi that enables owners of cell phones, laptop computers, and similar devices to connect wirelessly to the Internet at home and at coffee shops and airports. A wireless WiFi router is a device that exchanges data over the Internet through the cable or another connection, and uses microwaves to exchange the data wirelessly with devices such as cell phones and computers. The term WiFi itself refers to the standards followed in modulating and analyzing the microwaves so that wireless routers and devices from different manufacturers work compatibly with one another. The computer data in each direction consist of sequences of binary zeros and ones, each corresponding to a binary bit. The microwaves are in the range of 2.4 GHz to 5.0 GHz range.
Other wireless technologies also use microwaves to provide everyday communications between devices. Bluetooth developed alongside WiFi as a standard for radio communication in the 2.4-GHz range between nearby devices, for example, to link to headphones and audio earpieces to devices such as radios, or a driver’s cell phone to a hands-free device to allow answering phone calls without fumbling directly with the cell phone.
Microwaves find use also in radio tagging, using RFID (radio frequency identification) technology. Examples are RFID tags attached to store merchandize, transponder for toll booths use attached to the windshield of a car, or even a chip embedded into a pet’s skin. The device responds to a microwave signal by emitting a signal of its own with encoded information, allowing stores to quickly ring up items at their cash registers, drivers to charge tolls to their account without stopping, and lost pets to be reunited with their owners. NFC (near field communication) works similarly, except it is much shorter range. Its mechanism of interaction is the induced magnetic field at microwave frequencies between two coils. Cell phones that have NFC capability and the right software can supply information for purchases using the cell phone instead of a physical credit card. The very short range of the data transfer is a desired security feature in this case.
Infrared Radiation
The boundary between the microwave and infrared regions of the electromagnetic spectrum is not well defined (Figure 16.6.1). Infrared radiation is generally produced by thermal motion, and the vibration and rotation of atoms and molecules. Electronic transitions in atoms and molecules can also produce infrared radiation. About half of the solar energy arriving at Earth is in the infrared region, with most of the rest in the visible part of the spectrum. About 23% of the solar energy is absorbed in the atmosphere, about 48% is absorbed at Earth’s surface, and about 29% is reflected back into space.
The range of infrared frequencies extends up to the lower limit of visible light, just below red. In fact, infrared means “below red.” Water molecules rotate and vibrate particularly well at infrared frequencies. Reconnaissance satellites can detect buildings, vehicles, and even individual humans by their infrared emissions, whose power radiation is proportional to the fourth power of the absolute temperature. More mundanely, we use infrared lamps, including those called quartz heaters, to preferentially warm us because we absorb infrared better than our surroundings.
The familiar handheld “remotes” for changing channels and settings on television sets often transmit their signal by modulating an infrared beam. If you try to use a TV remote without the infrared emitter being in direct line of sight with the infrared detector, you may find the television not responding. Some remotes use Bluetooth instead and reduce this annoyance.
Visible Light
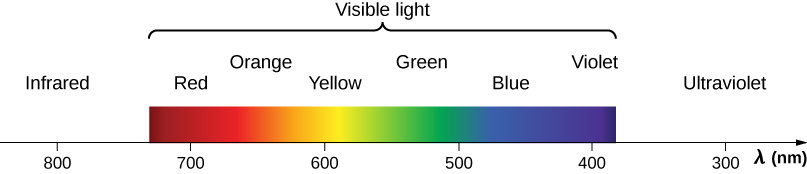
Visible light is the narrow segment of the electromagnetic spectrum between about 400 nm and about 750 nm to which the normal human eye responds. Visible light is produced by vibrations and rotations of atoms and molecules, as well as by electronic transitions within atoms and molecules. The receivers or detectors of light largely utilize electronic transitions.
Red light has the lowest frequencies and longest wavelengths, whereas violet has the highest frequencies and shortest wavelengths (Figure 16.6.4). Blackbody radiation from the Sun peaks in the visible part of the spectrum but is more intense in the red than in the violet, making the sun yellowish in appearance.
Living things - plants and animals - have evolved to utilize and respond to parts of the electromagnetic spectrum in which they are embedded. We enjoy the beauty of nature through visible light. Plants are more selective. Photosynthesis uses parts of the visible spectrum to make sugars.
Ultraviolet Radiation
Ultraviolet means “above violet.” The electromagnetic frequencies of ultraviolet radiation (UV) extend upward from violet, the highest-frequency visible light. The highest-frequency ultraviolet overlaps with the lowest-frequency X-rays. The wavelengths of ultraviolet extend from 400 nm down to about 10 nm at its highest frequencies. Ultraviolet is produced by atomic and molecular motions and electronic transitions.
UV radiation from the Sun is broadly subdivided into three wavelength ranges: UV-A (320–400 nm) is the lowest frequency, then UV-B (290–320 nm) and UV-C (220–290 nm). Most UV-B and all UV-C are absorbed by ozone (O3) molecules in the upper atmosphere. Consequently, 99% of the solar UV radiation reaching Earth’s surface is UV-A.
Sunburn is caused by large exposures to UV-B and UV-C, and repeated exposure can increase the likelihood of skin cancer. The tanning response is a defense mechanism in which the body produces pigments in inert skin layers to reduce exposure of the living cells below.
As examined in a later chapter, the shorter the wavelength of light, the greater the energy change of an atom or molecule that absorbs the light in an electronic transition. This makes short-wavelength ultraviolet light damaging to living cells. It also explains why ultraviolet radiation is better able than visible light to cause some materials to glow, or fluoresce.
Besides the adverse effects of ultraviolet radiation, there are also benefits of exposure in nature and uses in technology. Vitamin D production in the skin results from exposure to UV-B radiation, generally from sunlight. Several studies suggest vitamin D deficiency is associated with the development of a range of cancers (prostate, breast, colon), as well as osteoporosis. Low-intensity ultraviolet has applications such as providing the energy to cause certain dyes to fluoresce and emit visible light, for example, in printed money to display hidden watermarks as counterfeit protection.
X-Rays
X-rays have wavelengths from about 10−8m to 10−12m. They have shorter wavelengths, and higher frequencies, than ultraviolet, so that the energy they transfer at an atomic level is greater. As a result, X-rays have adverse effects on living cells similar to those of ultraviolet radiation, but they are more penetrating. Cancer and genetic defects can be induced by X-rays. Because of their effect on rapidly dividing cells, X-rays can also be used to treat and even cure cancer.
The widest use of X-rays is for imaging objects that are opaque to visible light, such as the human body or aircraft parts. In humans, the risk of cell damage is weighed carefully against the benefit of the diagnostic information obtained.
Gamma Rays
Soon after nuclear radioactivity was first detected in 1896, it was found that at least three distinct types of radiation were being emitted, and these were designated as alpha, beta, and gamma rays. The most penetrating nuclear radiation, the gamma ray γ -ray) was later found to be an extremely high-frequency electromagnetic wave.
The lower end of the γ-ray frequency range overlaps the upper end of the X-ray range. Gamma rays have characteristics identical to X-rays of the same frequency—they differ only in source. The name “gamma rays” is generally used for electromagnetic radiation emitted by a nucleus, while X-rays are generally produced by bombarding a target with energetic electrons in an X-ray tube. At higher frequencies, γ-rays are more penetrating and more damaging to living tissue. They have many of the same uses as X-rays, including cancer therapy. Gamma radiation from radioactive materials is used in nuclear medicine.
Use this simulation to explore how light interacts with molecules in our atmosphere.
- Explore how light interacts with molecules in our atmosphere.
- Identify that absorption of light depends on the molecule and the type of light.
- Relate the energy of the light to the resulting motion.
- Identify that energy increases from microwave to ultraviolet.
- Predict the motion of a molecule based on the type of light it absorbs.
How do the electromagnetic waves for the different kinds of electromagnetic radiation differ?
- Answer
-
They fall into different ranges of wavelength, and therefore also different corresponding ranges of frequency.


