2.8: Fitting a Conic Section Through Five Points
\(\text{FIGURE II.38}\)
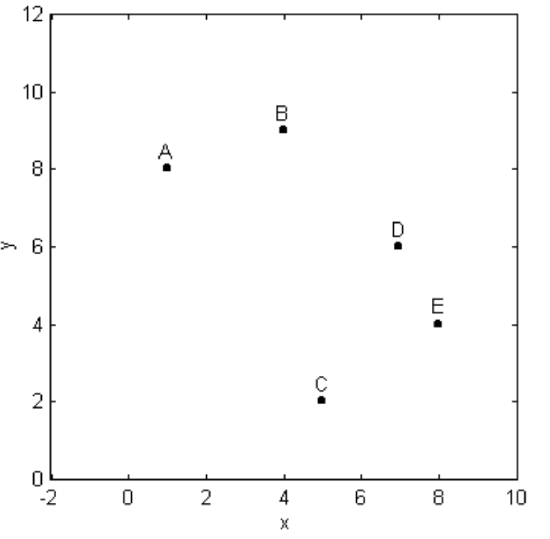
Figure \(\text{II.38}\) shows the five points \(\text{A}(1,8), \ \text{B}(4,9), \ \text{C}(5,2), \ \text{D}(7,6), \ \text{E}(8,4)\). Problem: Draw a conic section through the five points.
The first thing to notice is that, since a conic section is of the form
\[ax^2 + 2hxy + by^2 + 2gx + 2fy + 1 = 0 \label{2.8.1} \tag{2.8.1}\]
(remember that there is no loss of generality by taking the constant term to be 1), five points are necessary and sufficient to define a conic section uniquely. One and only one conic section can be drawn through these five points. We merely have to determine the five coefficients. The most direct (but not the fastest or most efficient) way to do this is to substitute each of the (x , y) pairs into the equation in turn, thus obtaining five linear equations in the five coefficients.
There is a better way.
We write down the equations for the straight lines \(\text{AB}, \ \text{CD}, \ \text{AC}\) and \(\text{BD}\). Let us call these equations \(α = 0, \ β = 0, \ γ = 0\) and \(δ = 0\) respectively (figure \(\text{II.39}\)).
Then \(αβ = 0\) is the equation that represents the two straight lines \(\text{AB}\) and \(\text{CD}\), and \(γδ = 0\) is the equation that represents the two straight lines \(\text{AC}\) and \(\text{BD}\). The equation \(αβ + λγδ = 0\), where \(λ\) is an arbitrary constant, is a second degree equation that represents any conic section that passes through the points \(\text{A}\), \(\text{B}\), \(\text{C}\) and \(\text{D}\). By inserting the coordinates of \(\text{E}\) in this equation, we can find the value of \(λ\) that forces the equation to go through all five points. This model of unclarity will become clear on following an actual calculation for the five points of the present example.
\(\text{FIGURE II.39}\)
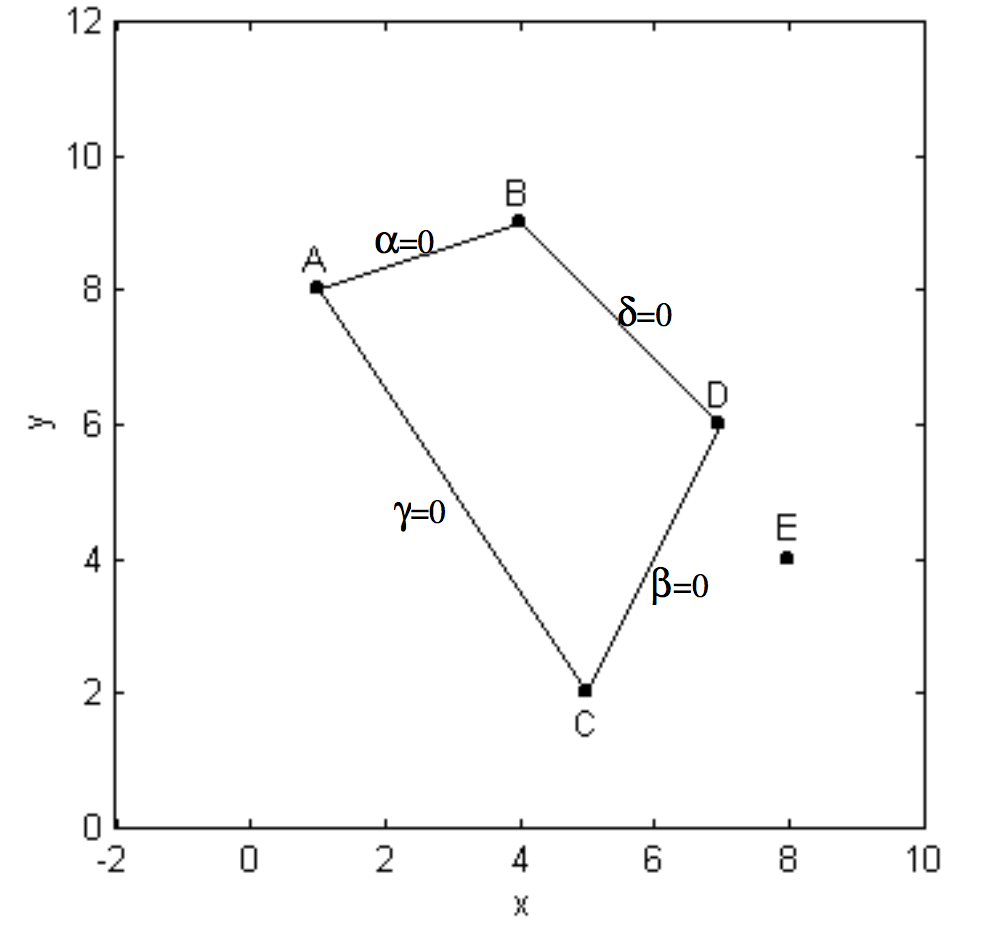
The four straight lines are
\(α=0: \quad x - 3y + 23 = 0\)
\(β=0: \quad 2x - y - 8 = 0\)
\(γ=0: \quad 3x + 2y - 19 = 0\)
\(δ=0: \quad x + y -13 = 0\)
The two pair of lines are
\(αβ=0: \quad 2x^2 - 7xy + 3y^2 + 38x + y -184 = 0\)
\(γδ=0: \quad 3x^2 + 5xy + 2y^2 -58x -45y +247 =0\)
and the family of conic sections that passes through \(\text{A, B, C}\) and \(\text{D}\) is
\(αβ + λγδ = 0:\)
\((2+3λ)x^2 - (7-5λ)xy + (3+2λ)y^2 + (38-58λ)x + (1-45λ)y - 184 + 247λ = 0.\)
Now substitute \(x = 8\), \(y = 4\) to force the conic section to pass through the point \(\text{E}\). This results in the value
\(λ=\frac{76}{13}.\)
The equation to the conic section passing through all five points is therefore
\(508x^2 + 578xy +382y^2 - 7828x - 6814y + 32760 = 0\)
We can, if desired, divide this equation by \(2\) (since all coefficients are even), or by \(32760\) (to make the constant term equal to \(1\)) but, to make the analysis that is to follow easier, I choose to leave the equation in the above form, so that the constants \(f\), \(g\) and \(h\) remain integers.
The constants have the values
\(a=508, b=382, c=32760, f=-3407, g=-3914, h=289\)
and the cofactors have the values
\(\bar a = 906 \ 671, \quad \bar b = 1 \ 322 \ 684, \quad \bar c = 110 \ 535\)
\(\bar f = 599 \ 610, \quad \bar g = 510 \ 525, \quad \bar h = 3 \ 867 \ 358\)
Let us consult the dichotomous table. The value of the determinant is \(∆ = a\bar{a} + h\bar{h} + g\bar{g} (\text{or} \ h\bar{h} + b\bar{b} + f\bar{f}, \ \text{or} \ g\bar{g} + f\bar{f} + c\bar{c}\); try all three sums to check for arithmetic mistakes). It comes to \(∆ = −419 \ 939 \ 520\), so we proceed to option \(5\). \(\bar{c} > 0\), so we proceed to option \(6\). \(a\) and \(∆\) have opposite signs, so we proceed to \(7\). \(a\) does not equal \(b\), nor is \(h\) equal to zero. Therefore we have an ellipse. It is drawn in figure \(\text{II.40}\).
\(\text{FIGURE II.40}\)
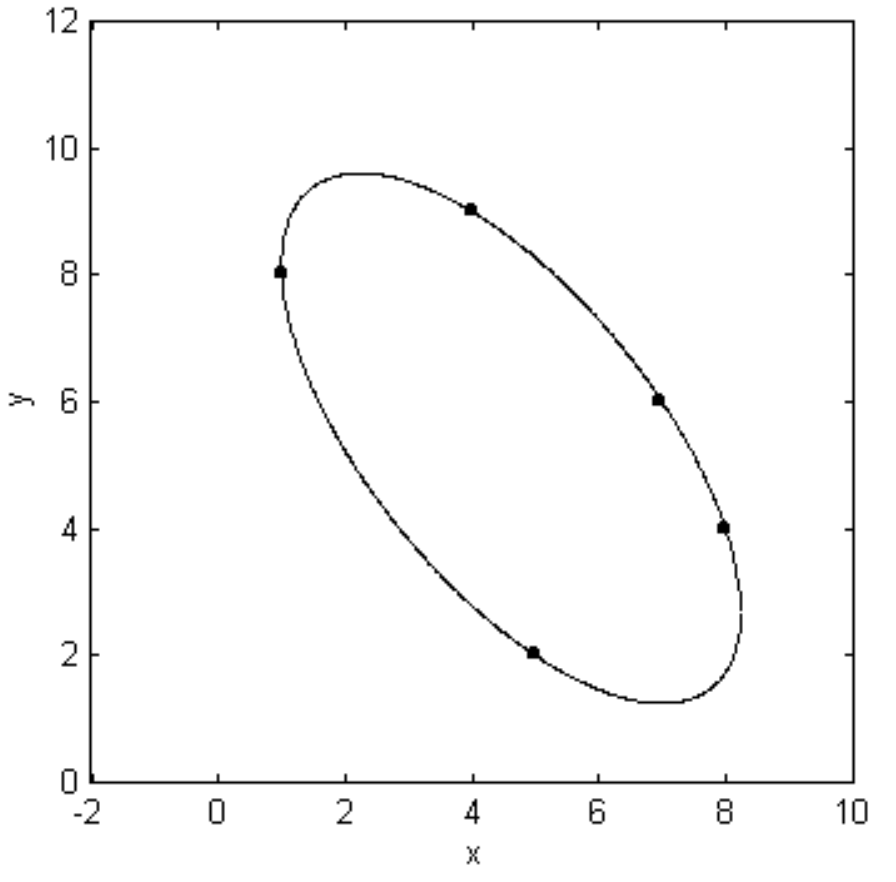
The centre of the ellipse is at \((4.619, \ 5.425)\), and its major axis is inclined at an angle \(128^\circ \ 51^\prime\) to the \(x\)-axis. If we now substitute \(x + 4.619\) for \(x\) and \(y + 5.425\) for \(y\), and then substitute \(x \cos 128^\circ 51^\prime + y \sin 128^\circ 51^\prime\) for the new value of \(x\) and \(−x \sin 128^\circ 51^\prime + y \cos 128^\circ 51^\prime\) for the new value of \(y\), the equation will assume its the familiar form for an ellipse referred to its axes as coordinate axes and its centre as origin.