2.6: Two Semicylindrical Electrodes

This section requires that the reader should be familiar with functions of a complex variable and conformal transformations. For readers not familiar with these, this section can be skipped without prejudice to understanding following chapters. For readers who are familiar, this is a nice example of conformal transformations to solve a physical problem.

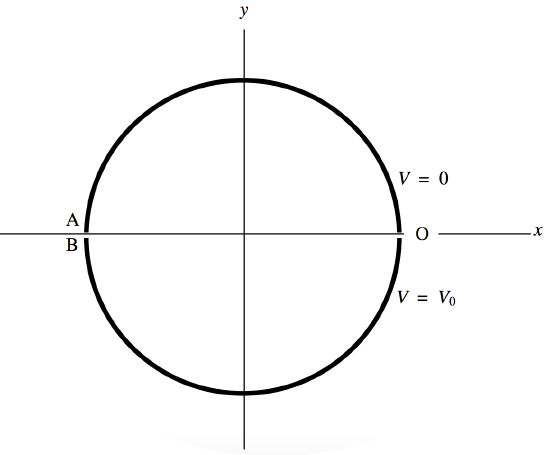
\(\text{FIGURE II.5}\)

We have two semicylindrical electrodes as shown in Figure \(II\).5. The potential of the upper one is 0 and the potential of the lower one is \(V_0\). We'll suppose the radius of the circle is 1; or, what amounts to the same thing, we'll express coordinates \(x\) and \(y\) in units of the radius. Let us represent the position of any point whose coordinates are (x , y) by a complex number \(z = x + iy\).

Now let \(w = u + iv\) be a complex number related to \(z\) by \(w=i\left (\frac{1-z}{1+z}\right )\); that is, \(z=\frac{1+ iw}{1- iw}\). Substitute \(w = u + iv \text{ and }z = x + iy\) in each of these equations, and equate real and imaginary parts, to obtain

\[\begin{align}\label{2.6.1}u&=\frac{2y}{(1+x)^2+y^2};\quad\quad &&v=\frac{1-x^2+y^2}{(1+x)^2+y^2};\\ x&=\frac{1-u^2-v^2}{u^2+(1+v)^2}; &&y=\frac{2u}{u^2+(1+v)^2}.\label{2.6.2}\end{align}\]

In that case, the upper semicircle \((V = 0)\) in the \(xy\)-plane maps on to the positive \(u\)-axis in the \(uv\)-plane, and the lower semicircle \((V = V_0)\) in the \(xy\)-plane maps on to the negative \(u\)-axis in the \(uv\)-plane. (Figure \(II\).6.) Points inside the circle bounded by the electrodes in the \(xy\)-plane map on to points above the \(u\)-axis in the \(uv\)-plane.

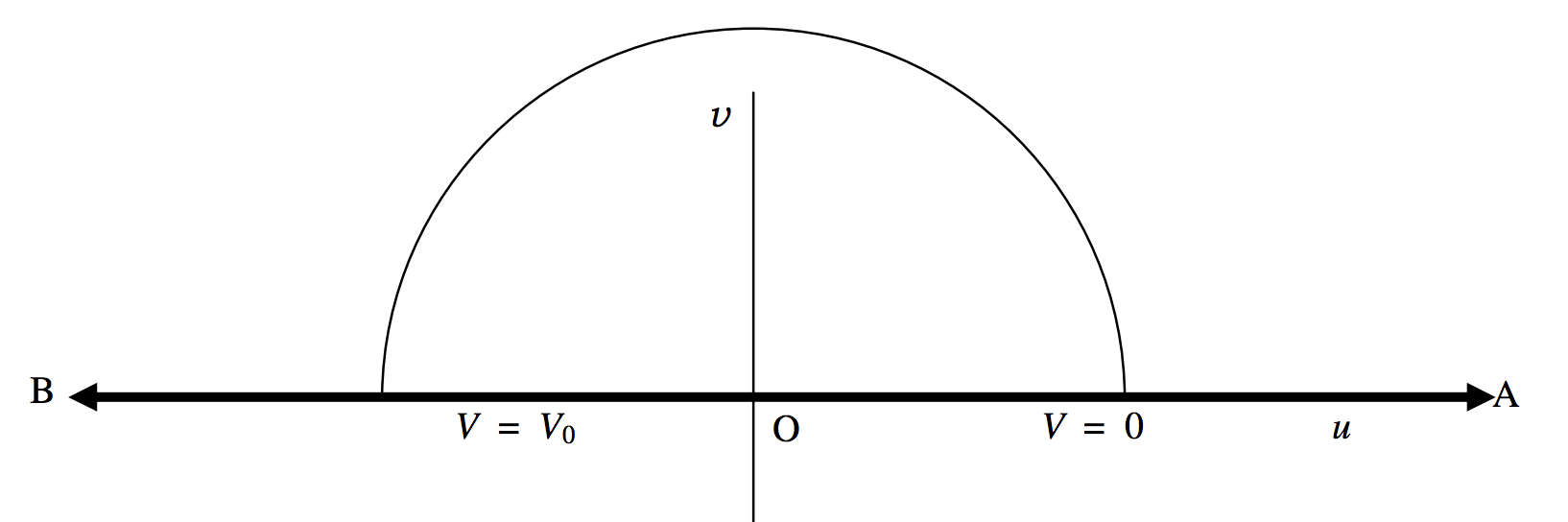
\(\text{FIGURE II.6}\)

In the \(uv\)-plane, the lines of force are semicircles, such as the one shown. The potential goes from 0 at one end of the semicircle to \(V_0\) at the other, and so equation to the semicircular line of force is

\[\label{2.6.3}\frac{V}{V_0}=\frac{\text{arg}\,w}{\pi}\]

or

\[\label{2.6.4}V=\frac{V_0}{\pi}\tan^{-1}(v/u).\]

The equipotentials (\(V\) = constant) are straight lines in the \(uv\)-plane of the form

\[\label{2.6.5}v=fu.\]

(You would prefer me to use the symbol \(m\) for the slope of the equipotentials, but in a moment you will be glad that I chose the symbol \(f\).)

If we now transform back to the \(xy\)-plane, we see that the equation to the lines of force is

\[\label{2.6.6}V=\frac{V_0}{\pi}\tan^{-1} \left (\frac{1-x^2-y^2}{2y}\right ).\]

and the equation to the equipotentials is

\[\label{2.6.7}1-x^2-y^2=2fy,\]

or

\[\label{2.6.8}x^2+y^2+2fy-1=0\]

Now aren't you glad that I chose \(f\) ? Those who are handy with conic sections (see Chapter 2 of Celestial Mechanics) will understand that the equipotentials in the \(xy\)-plane are circles of radii \(\sqrt{f^2 + 1}\), whose centres are at \((0 , \pm f )\), and which all pass through the points \((\pm 1 , 0)\). They are drawn as blue lines in Figure \(II\).7. The lines of force are the orthogonal trajectories to these, and are of the form

\[\label{2.6.9}x^2+y^2+2gy+1=0\]

These are circles of radii \(\sqrt{g^2 −1}\) and have their centres at \((0 , \pm g)\). They are shown as dashed red lines in Figure \(II\).7.

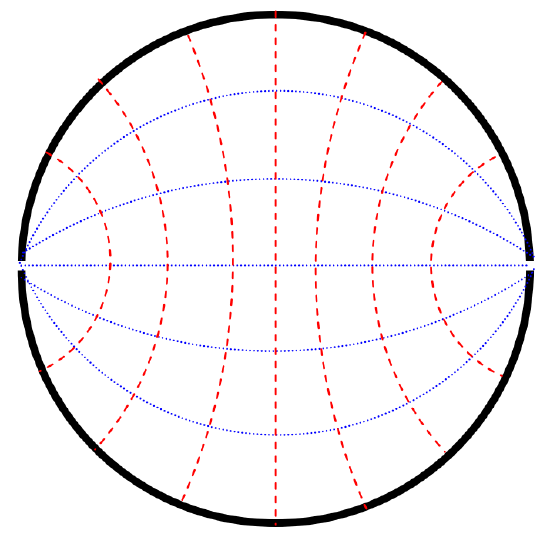
\(\text{FIGURE II.7}\)